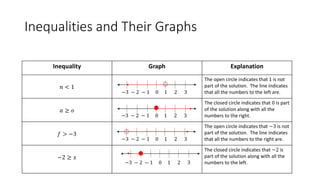
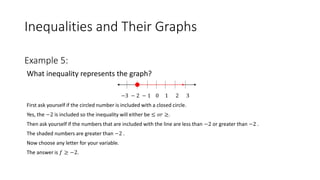
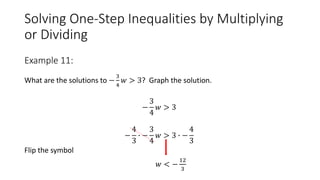
The document explains solving inequalities, which are mathematical statements that compare expressions using symbols such as <, >, ≤, and ≥. It distinguishes between equations, which have definite solutions, and inequalities, which have infinite solutions and can be represented on a number line. The text includes examples and methods for graphing inequalities as well as solving one-step, multi-step, and compound inequalities.