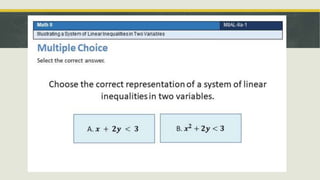
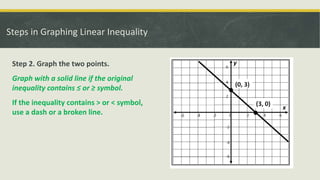
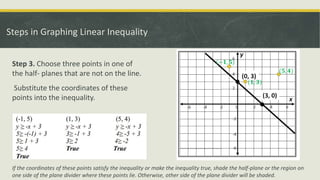
This document discusses linear inequalities in two variables. It explains that a linear inequality can be written in forms such as Ax + By > C, Ax + By < C, Ax + By ≥ C, or Ax + By ≤ C. It contrasts linear equations, which use the equal sign, from linear inequalities, which use various inequality signs. Examples of graphing linear inequalities on a coordinate plane are provided, including the steps of replacing inequality signs with equals signs, plotting points, and shading the appropriate half-plane based on tested points. Solving word problems involving linear inequalities in two variables is also demonstrated through examples.

1. Illustrating Linear
Inequalities in Two Variables
Quarter 2 – Module 1

2. Linear Inequality in Two Variables
It consists of two variables working together.
It can be written in the following forms:
𝑨𝒙 + 𝑩𝒚 > 𝑪
𝑨𝒙 + 𝑩𝒚 < 𝑪
𝑨𝒙 + 𝑩𝒚 ≥ 𝑪
𝑨𝒙 + 𝑩𝒚 ≤ 𝑪

3. Linear Equation vs Linear Inequality
It is a Mathematical
sentence which shows that
the two quantities have
equal values.
It is a Mathematical
sentence which shows that
two quantities have
different or unequal value.

4. Linear Equation vs Linear Inequality
Symbol used
=
Symbol used
≠
>
<
≥
≤
not equal
greater than
Less than
Greater than or equal to
Less than or equal to

5. x + 3y <10
2p – 5r ≥ 24
4b + 3c > 10
𝒙 𝒑𝒍𝒖𝒔 𝒕𝒉𝒓𝒆𝒆 𝒚 𝒊𝒔 𝒍𝒆𝒔𝒔 𝒕𝒉𝒂𝒏 𝟏𝟎
𝑻𝒘𝒐 𝒑 𝒎𝒊𝒏𝒖𝒔 𝒇𝒊𝒗𝒆 𝒓 𝐢𝐬 𝐠𝐫𝐞𝐚𝐭𝐞𝐫 𝐭𝒉𝒂𝒏 𝒐𝒓 𝒆𝒒𝒖𝒂𝒍 𝒕𝒐 𝒕𝒘𝒆𝒏𝒕𝒚 − 𝒇𝒐𝒖𝒓.
𝑭𝒐𝒖𝒓 𝒃 𝒑𝒍𝒖𝒔 𝒕𝒉𝒓𝒆𝒆 𝒄 𝒊𝒔 𝒈𝒓𝒆𝒂𝒕𝒆𝒓 𝒕𝒉𝒂𝒏 𝒕𝒆𝒏.

6. Linear Inequality in Two Variables
Uses the inequality signs >, <, ≥, ≤.
It divides the coordinate plane in two parts.
One-half of the side is where the solutions of the
linear inequality lies. It is called the half-plane.

7. Solution of Linear Inequality
The solution of the linear inequality is the ordered
pair 𝒙, 𝒚 that satisfies the inequality when the
values of 𝒙 and 𝒚 are substituted in the inequality.
The ordered pair is in a half-plane of a rectangular
coordinate system and is usually shaded.
The boundary of the plane is determined using a solid
or a dashed line.

8. Graph of Linear Inequality (≤, ≥)

9. Graph of Linear Inequality (≤, ≥)
The points on the solid line are included in the
solution of the linear inequality.
It will satisfy the inequality.

10. Graph of Linear Inequality (<, >)

11. Graph of Linear Inequality (<, >)
The points on the dashed line are not included in the
solution of the linear inequality.
It will not satisfy the inequality.

12. v

13. v

14. v

15. Graph of a Linear
Inequality in Two
Variables

16. Steps in Graphing Linear Inequality
Step 1) Replace the inequality
symbol with an equal sign. The
resulting equation becomes the
plane divider.
Example:
𝒚 ≥ −𝒙 + 𝟑
Step 2) To graph the equation y =-
x + 3, assign some values of x and
y. In this example, we will
Let 𝑥 = 0
𝑦 = −𝑥 + 3
𝑦 = 0 + 3
𝑦 = 3
0,3
Let 𝑦 = 0
𝑦 = −𝑥 + 3
0 = −𝑥 + 3
𝑥 = +3
𝑥 = 3
3,0
𝒚 = −𝒙 + 𝟑

17. Steps in Graphing Linear Inequality
Step 2. Graph the two points.
Graph with a solid line if the original
inequality contains ≤ or ≥ symbol.
If the inequality contains > or < symbol,
use a dash or a broken line.

18. Steps in Graphing Linear Inequality
Step 3. Choose three points in one of
the half- planes that are not on the line.
Substitute the coordinates of these
points into the inequality.
If the coordinates of these points satisfy the inequality or make the inequality true, shade the half-plane or the region on
one side of the plane divider where these points lie. Otherwise, other side of the plane divider will be shaded.
(−𝟏, 𝟓)
(𝟏, 𝟑)
(𝟓, 𝟒)

19. Steps in Graphing Linear Inequality 𝒚 ≥ −𝒙 + 𝟑

20. Solving Problems
involving Linear
Inequalities in Two
Variables

21. 2𝑥 + 𝑦 > 4 𝑦 < 𝑥 − 3
𝑥 + 3𝑦 ≥ 12
𝑥 + 2𝑦 ≤ 10

22. Review

23. Graph of
Linear
Inequalities
Review

24. Review

25. Review
> < ≥ ≤ Is less than
Is more than
Is at most
Is at least
Is no more than
Smaller than
Maximum
Minimum
Is more
than
Is less
than
Smaller
than
Is at least
Minimum
Is at most
Maximum
Is no
more than

26. ACTIVITY
𝒇 + 𝒕 > 𝟒𝟓
𝒎 − 𝒓 ≥ 𝟓
𝟐𝒌 + 𝟑 < 𝒇
𝒇 + 𝒆 ≤ 𝟑𝟎𝟎𝟎
𝟐𝒈 < 𝒚

27. Steps in Solving Problems Involving Linear Inequalities
in Two Variables
Step 1: Identify the words needed to be represented with
variables/symbols.
Step 2: Translate the statement into mathematical expression.
Step 3: Identify what is asked in the problem then solve.

28. Illustrative Example 1.
Julius has a job as an
appliance salesman. He earns a
commission of Php P600 for
each washing machine he sells
and P800 for each refrigerator
he sells. He needs to earn a
commission of at least
P10,000.
Solution
Step 1 Identify the words
needed to be represented
with variables/symbols.
Let w = number of washing
machines Julius sells
Let r = number of
refrigerators Julius sells

29. Illustrative Example 1.
Julius has a job as an
appliance salesman. He earns a
commission of Php P600 for
each washing machine he sells
and P800 for each refrigerator
he sells. He needs to earn a
commission of at least
P10,000.
Solution
Step 2: Translate the
statement into
mathematical expression.
𝟔𝟎𝟎𝒘 + 𝟖𝟎𝟎𝒓 ≥ 𝟏𝟎𝟎𝟎𝟎

30. Illustrative Example 1.
If Julius was able to
sell 6 washing machines,
what could be the least
number of refrigerators
that he needs to sell in
order to reach the
commission of at least
P10,000?
Solution
Step 3: Identify what is
asked in the problem then
solve.
𝟔𝟎𝟎𝒘 + 𝟖𝟎𝟎𝒓 ≥ 𝟏𝟎𝟎𝟎𝟎
𝟔𝟎𝟎(𝟔) + 𝟖𝟎𝟎𝒓 ≥ 𝟏𝟎𝟎𝟎𝟎
𝟑𝟔𝟎𝟎 + 𝟖𝟎𝟎𝒓 ≥ 𝟏𝟎𝟎𝟎𝟎
𝟖𝟎𝟎𝒓 ≥ 𝟏𝟎𝟎𝟎𝟎 − 𝟑𝟔𝟎𝟎
𝟖𝟎𝟎𝒓 ≥ 𝟔𝟒𝟎𝟎
𝟖𝟎𝟎𝒓
𝟖𝟎𝟎
≥
𝟔𝟒𝟎𝟎
𝟖𝟎𝟎
𝒓 ≥ 𝟖
The least number of refrigerators that Julius needs to sell
is 8 pcs in order to earn a commission of at least P10,000.

31. Illustrative Example 2.
The difference between the
height of Mark (𝑚) and Rhea (𝑟) is at
least 5 cm. If Rhea’s height is 160
cm, what is the least possible height
of Mark?
Solution

32. Illustrative Example 3.
In a week, Martinez family
spends less than 𝑃3,021 for food (𝑓)
and educational expense (𝑒).
Suppose the family spent PhP 1000
for education, what could be the
family’s maximum possible
expenses for food?
Solution

33. Illustrative Example 4.
Your parents give you a
weekly allowance greater than 𝑃
200. The allowance is budgeted for
your food and school needs. If you
allotted 𝑃70 for your school needs,
what would be the minimum budget
for your food?
Solution

34. 15
15

35. 1. The difference between Lian’s height and William’s height is not more than 4
inches. Suppose Lian’s height is 65 inches, what could be the height of William?
2. Sean plans to sell hotdogs for P10 and hard-boiled eggs for P7. If he sells 22
hotdogs, what is the maximum number of hard-boiled eggs he should sell to
have total sales of at least P300.00?
3. In June, the electric bill of Matalino family is at most P90 lower than the
previous month. If the previous bill marked P1430, at most how much does the
present bill cost?

36. Linear Equation and Linear Inequality

37. Linear Equation and Linear Inequality