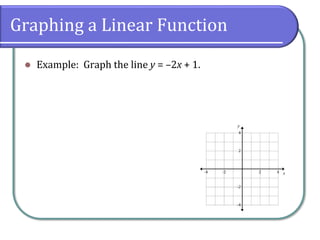
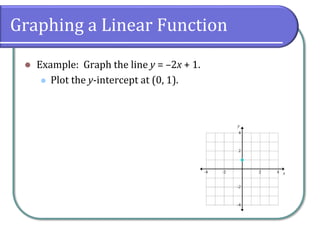
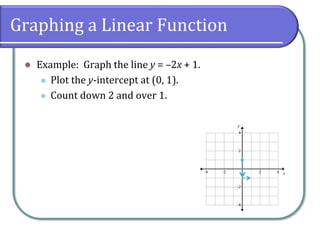
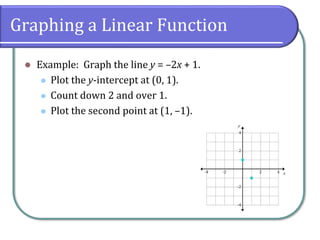
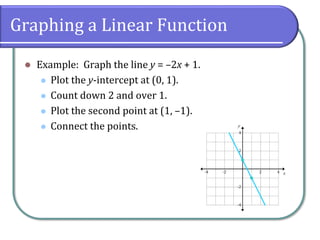
This document covers the concepts of linear functions, including their properties, definitions, and different forms such as standard and slope-intercept forms. It explains how to identify functions, determine domains and ranges, and calculate the slope between points, along with graphing methods. The document also highlights the historical context of function notation and identifies conditions under which relations can be classified as functions.

1. Linear Functions
Chapter 2 Graphs and Functions

2. Concepts & Objectives
⚫ Function Properties
⚫ Identify whether a relation is a function
⚫ Identify the domain and range of a given function
⚫ Linear Functions
⚫ Calculate the slope between two points
⚫ Graph a linear function

3. Functions
⚫ A relation is a set of ordered pairs.
⚫ A function is a relation in, for each distinct value of the
first component of the ordered pairs, there is exactly one
value of the second component.
⚫ More formally:
If A and B are sets, then a function f from A to B
(written f: A → B)
is a rule that assigns to each element of A
a unique element of set B.

4. Functions (cont.)
⚫ The set A is called the domain of the function f
⚫ Every element of A must be included in the function.
⚫ The set B is called the codomain of f
⚫ The subset of B consisting of those elements that are
images under the function f is called the range.
⚫ The range and the codomain may or may not be the
same.

5. Functions (cont.)
⚫ In terms of ordered pairs, a function is the set of ordered
pairs (A, f (A)).
⚫ Historical note: The notation f (x) for a function of a
variable quantity x was introduced in 1748 by Leonhard
Euler in his text Algebra, which was the forerunner of
today’s algebra texts. Many other mathematical symbols
in use today (such as e and ) were introduced by Euler
in his writings.

6. Functions (cont.)
⚫ For the most part, we use f (x) and y interchangeably to
denote a function of x, but there are some subtle
differences.
⚫ y is the output variable, while f (x) is the rule that
produces the output variable.
⚫ An equation with two variables, x and y, may not be a
function at all.
Example: is a circle, but not a function+ =2 2
4x y

7. Linear Functions
⚫ A function f is a linear function if, for a and b  ,
⚫ If a ≠ 0, the domain and the range of a linear function are
both .
⚫ The slope of a linear function is defined as the rate of
change or the ratio of rise to run.
( )f x ax b= +
( ),− 
The slope m of the line through the
points and is( )1 1,x y ( )2 2,x y
2 1
2 1
rise
run
y y
m
x x
−
= =
−

8. Linear Functions (cont.)
⚫ A linear function can be written in one of the following
forms:
⚫ Standard form: Ax + By = C, where A, B, C  , A 0,
and A, B, and C are relatively prime
⚫ Point-slope form: y – y1 = m(x – x1), where m   and
(x1, y1) is a point on the graph
⚫ Slope-intercept form: y = mx + b, where m, b  
⚫ You should recall that in slope-intercept form, m is the
slope and b is the y-intercept (where the graph crosses
the y-axis).
⚫ If A = 0, then the graph is a horizontal line at y = b.

9. Linear Functions (cont.)
⚫ Let’s take another look at the standard form:
If B = 0 (the coefficient of the y term), we end up with
which is undefined. This is not good.
+ =
= − +
= − +
Ax By C
By Ax C
A C
y x
B B
= − + ,
0 0
A C
y x

10. Linear Functions (cont.)
⚫ Since we cannot divide by 0, we say that a line of the
form x = a has no slope, and is a vertical line.
⚫ Technically, a vertical line is not a function at all,
because one value of x has more than one y value
(actually an infinite number of y values), but since it is a
straight line, we include it along with the linear
functions.

11. Graphing a Linear Function
To graph a line:
⚫ If you are only given two points, plot them and draw a
line between them.
⚫ If you are given a point and a slope:
⚫ Plot the point.
⚫ From the point count the rise and the run of the slope
and mark your second point.
⚫ Connect the two points.
⚫ If the slope is negative, pick either the rise or the run
to go in a negative direction, but not both.

12. Graphing a Linear Function
⚫ Example: Graph the line y = –2x + 1.

13. Graphing a Linear Function
⚫ Example: Graph the line y = –2x + 1.
⚫ Plot the y-intercept at (0, 1).

14. Graphing a Linear Function
⚫ Example: Graph the line y = –2x + 1.
⚫ Plot the y-intercept at (0, 1).
⚫ Count down 2 and over 1.

15. Graphing a Linear Function
⚫ Example: Graph the line y = –2x + 1.
⚫ Plot the y-intercept at (0, 1).
⚫ Count down 2 and over 1.
⚫ Plot the second point at (1, –1).

16. Graphing a Linear Function
⚫ Example: Graph the line y = –2x + 1.
⚫ Plot the y-intercept at (0, 1).
⚫ Count down 2 and over 1.
⚫ Plot the second point at (1, –1).
⚫ Connect the points.

17. Classwork
⚫ College Algebra
⚫ Page 226: 26-32 (even), page 163: 28-40 (even),
page 155: 36-48 (even)