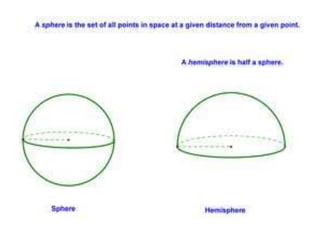
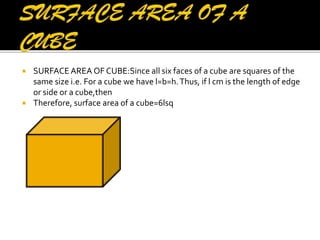
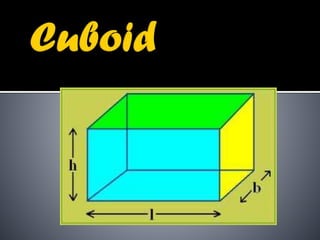
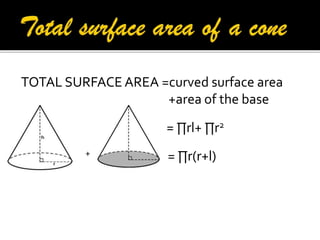
1. The document defines various 3D shapes including cubes, cuboids, cylinders, cones, spheres, and hemispheres. 2. It provides the formulas to calculate the surface area and volume of each shape. For cubes, cuboids, cylinders and cones it gives the formulas for total surface area. For spheres and hemispheres it provides the formulas for total surface area, curved surface area, and volume. 3. The document was created collaboratively by several students, with each person responsible for explaining different shapes.

1. AND VOLUMES

4. 

DEFINATION:A cuboid whose length ,breadth, height is called a cube.
SOLID CUBE:A solid cube is the part of the space enclosed by six faces of
the cube.

5. 

SURFACE AREA OF CUBE:Since all six faces of a cube are squares of the
same size i.e. For a cube we have l=b=h. Thus, if l cm is the length of edge
or side or a cube,then
Therefore, surface area of a cube=6lsq

6. 
I.
II.
III.
Lateral surface area of cube=4(edge)sq
Volume of cube=(edge) cubic
L.S.A of a cuboid =2 (l + b) h
T.S.A of a cuboid =2(lb+bh+lh)
Volume of the cuboid =lbh
T.S.A of a cube =6a2< Total surface area of a cube, sum areas of all the
faces of a cube >

7. 
FaceAlso called facets or sides. A cube has six faces which are all squares, so each
face has four equal sides and all four interior angles are right angles.
See Definition of a square. In the figure above, drag the 'explode' slider to see the
faces separated for clarity.


EdgeA line segment formed where two edges meet. A cube has 12
edges. Because all faces are squares and congruent to each other, all 12
edges are the same length.
VertexA point formed where three edges meet. A cube has 8 vertices.

9. A
solid which has six
rectangular faces at right
angles to each other.

10. Surface of the cuboid without the top
= 2 (bh + hl) + lb
SURFACE AREA OF CUBOID WITHOUT THE TOP AND
THE BOTTOM
= 2 (bh + hl)

11. AREA OF RECTANGLE 1 = (l x h) +
AREA OF RECTANGLE 2 = (l x b) +
AREA OF RECTANGLE 3 = (l x h) +
AREA OF RECTANGLE 4 = (l x b) +
AREA OF RECTANGLE 5 = (b x h) +
AREA OF RECTANGLE 6 = (b x h)
= 2 (l x b) + 2 (b x h) + 2(l x h)
= 2 (lb + bh + hl)

12. 

Volume is the space occupied by an object.
Volume is also referred to capacity of an object.
THUS,
VOLUME OF CUBOID = BASE AREA x HEIGHT
= (l x b) x h
=lxbxh
VOLUME OF CUBOID = l x b x h

14. 
A cylinder is one of the most basic curvilinear
geometric shapes, the surface formed by the
points at a fixed distance from a given line
segment, the axis of the cylinder. The solid
enclosed by this surface and by two planes
perpendicular to the axis is also called a
cylinder.

15. 

TSA of a cylinder = area of the base + area of
top + CSA of the cylinder
= ∏r2 + ∏r2 + 2∏rh
= 2∏r2 + 2∏rh
= 2∏r(r + h)
Where, r is the radius
h is the height of the cylinder

16. 


Volume of the cylinder = area of the base x
height
= r2 x h
= ∏r2h
Volume of hollow cylinder = ∏(R2 - r2) h
Where, r is the radius and h is the height

19. 
A cone is a three-dimensional geometric
shape that tapers smoothly from a flat base
(usually circular) to a point called the apex or
vertex.

20. when we cut a cone from its slant height
curved surface area of cone =area of sector
=1/2 *l *(2 ∏r)
= ∏r l

21. TOTAL SURFACE AREA =curved surface area
+area of the base
= ∏rl+ ∏r2
+
= ∏r(r+l)

22. WHEN WE
TAKE A
CONE AND
A
CYLINDER
OF SAME
HEIGHT
AND
RADIUS WE
GET

24. 1.
A sphere is a perfectly round geometrical object in three-dimensional space.
Like a circle, which is in two dimensions in a mathematical sense, a sphere is
the set of points that are all the same distance r from a given point in threedimensional space. This distance r is the radius of the sphere, and the given
point is the center of the sphere. The maximum straight distance through
the sphere passes through the centre and is thus twice the radius; it is the
diameter.
2. Hemisphere refers to the equal halves of the sphere and can
also be called the 3d design for a semi-circle.

25. 


When we talk about
painting or polishing the
surface it is related to the
surface area.
Surface-Area (TSA) = 4∏r2
Where,
‘r’ is the radius
from the center to surface.

26. 


TSA of hemisphere = 3∏r2
CSA of hemisphere = 2∏r2
Where, ‘r’ is the radius.

27. 


When we talk about the air in the solid or
want to count the no. of small object from
the bigger one then it is related to the
volume.
Volume of the sphere = 4/3∏r3
Where, r is the radius.

28. 

Volume of the Hemisphere = 2/3∏r3
Where, r is the radius.

30.  Cube – by Stuti Somani
 Cuboid –by Niriksha Mogaveera
 Cylinder – by Aditya Warrior
 Cone – by Shreyans Maliwal
 Sphere and Hemisphere-by Pakshal
 Animation– by Shreyans Maliwal
Shah