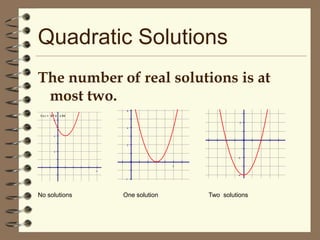
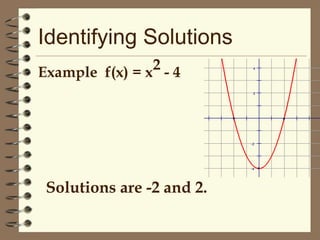
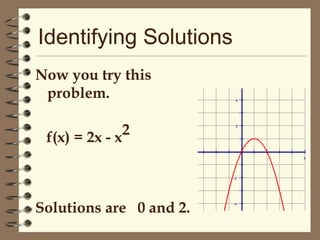
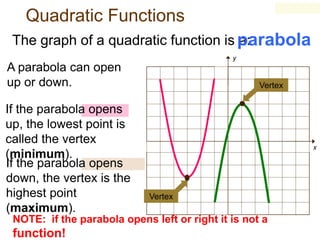
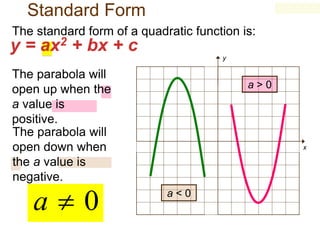
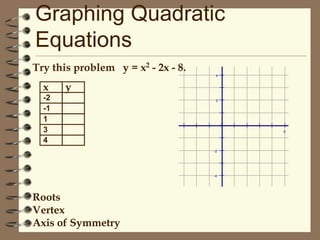
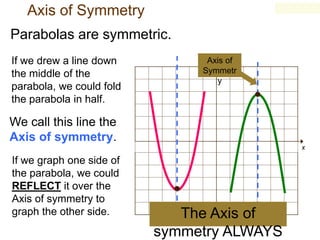
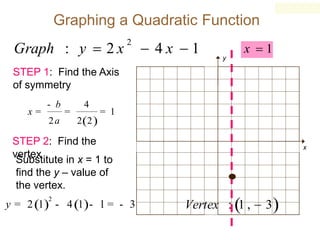
1) This document discusses how to solve quadratic equations by graphing, including identifying the terms of a quadratic equation, finding the solutions by graphing, and graphing quadratic functions. 2) The key steps for graphing a quadratic function are to find the axis of symmetry using the standard form equation, find the vertex point, and find two other points to reflect across the axis of symmetry to complete the parabolic graph. 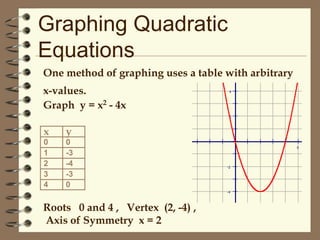3) An example problem walks through graphing the quadratic equation y = x^2 - 4x by first finding the roots, vertex, and axis of symmetry, and then constructing a table to plot points and graph the parabola.

1. Solving
Quadratic Equations
by Graphing

2. Quadratic Equation
y = ax2 + bx + c
2 is the quadratic term.
ax
bx is the linear term.
c is the constant term.
The highest exponent is two;
therefore, the degree is two.

3. Identifying Terms
2-7x+1
Example f(x)=5x
Quadratic term 5x2
Linear term
-7x
Constant term 1

4. Identifying Terms
2-3
Example f(x) = 4x
2
4x
Quadratic term
Linear term
0
Constant term -3

5. Identifying Terms
Now you try this
problem.
2 - 2x + 3
f(x) = 5x
quadratic term
linear term
constant term
5x2
-2x
3

6. Quadratic Solutions
The number of real solutions is at
most two.
6
f x  =
x 2 -2
 x +5
6
2
4
4
-5
2
5
2
-2
5
5
-4
-2
-2
No solutions
One solution
Two solutions

7. Quadratic Function
y = ax2 + bx +
c
Quadratic Term
Linear Term
Constant Term
2 – 3? 0x
What is the linear term of y = 4x
2- 5x ? -5x
What is the linear term of y = x
2 – 5x?
What is the constant term of y = x
0
Can the quadratic term be zero? No!

8. Solving Equations
When we talk about solving these
equations, we want to find the value
of x when y = 0. These values,
where the graph crosses the x-axis,
are called the x-intercepts.
These values are also referred to as
solutions, zeros, or roots.

9. Identifying Solutions
2-4
Example f(x) = x
4
2
-5
-2
-4
Solutions are -2 and 2.

10. Identifying Solutions
Now you try this
problem.
2
f(x) = 2x - x
4
2
5
-2
Solutions are 0 and 2.
-4

11. Quadratic Functions
The graph of a quadratic function is parabola
a:
y
A parabola can open
up or down.
If the parabola opens
up, the lowest point is
called the vertex
(minimum).
If the parabola opens
down, the vertex is the
highest point
(maximum).
Vertex
x
Vertex
NOTE: if the parabola opens left or right it is not a
function!

12. Standard Form
The standard form of a quadratic function is:
y = ax2 + bx + c
y
The parabola will
open up when the
a value is
positive.
The parabola will
open down when
the a value is
negative.
a0
a>0
x
a<0

13. Axis of Symmetry
Parabolas are symmetric.
If we drew a line down
the middle of the
parabola, we could fold
the parabola in half.
y
Axis of
Symmetr
y
We call this line the
Axis of symmetry.
x
If we graph one side of
the parabola, we could
REFLECT it over the
Axis of symmetry to
graph the other side.
The Axis of
symmetry ALWAYS

14. Finding the Axis of Symmetry
When a quadratic function is in standard
form
2
y = ax + bx + c,
the equation of the Axis of
symmetry is
This is best read as …
x
b
2a
‘the opposite of b divided by the quantity of 2
times a.’
2
Find the Axis of symmetry for y = 3x – 18x
a=3
b = -18+ 7
The Axis
18
18
x

2 3 
6
3
of
symmetry
is x = 3.

15. Finding the Vertex
The Axis of symmetry always goes through the
Vertex
_______. Thus, the Axis of symmetry
X-coordinate
gives us the ____________ of the vertex.
Find the vertex of
y = -2x2 + 8x - 3
STEP 1: Find the Axis of symmetry
x
b
a = -2
b=8
2a
x 
8
2( 2)

8
4
 2
The xcoordinate
of the
vertex is 2

16. Finding the Vertex
Find the vertex of
y = -2x2 + 8x - 3
STEP 1: Find the Axis of symmetry
x
b

2a
8
2(  2)

8
4
2
STEP 2: Substitute the x – value into the original
equation to find the y –coordinate of the vertex.
y  2
 2
2
2 
8
 4   16
  8  16  3
 5
2  3
 3
The
vertex
is (2 , 5)

17. Graphing a Quadratic Function
There are 3 steps to graphing a parabola in
standard form.
x
STEP 1: Find the Axis of symmetry using:
b
2a
STEP 2: Find the vertex
STEP 3: Find two other points and reflect them
across the Axis of symmetry. Then connect the
five points with a smooth curve.
MAKE A TABLE
using x – values close to
the Axis of symmetry.

18. Graphing a Quadratic Function
Graph : y  2 x
2
 4x 1
y
x 1
STEP 1: Find the Axis
of symmetry
x=
- b
2a
=
4
2 (2 )
= 1

STEP 2: Find the
vertex
Substitute in x = 1 to
find the y – value of
the vertex.
2
y = 2 (1) - 4 (1) - 1 = - 3
x
Vertex : 1 ,  3 

19. Graphing Quadratic
Equations
The graph of a quadratic equation is a
parabola.
The roots or zeros are the x-intercepts.
The vertex is the maximum or
minimum point.
All parabolas have an axis of
symmetry.

20. Graphing Quadratic
Equations
One method of graphing uses a table with arbitrary
x-values.
Graph y = x2 - 4x
4
2
x
y
0
1
2
3
4
0
-3
-4
-3
0
5
-2
-4
Roots 0 and 4 , Vertex (2, -4) ,
Axis of Symmetry x = 2

21. Graphing Quadratic
Equations
Try this problem y = x2 - 2x - 8.
4
x
y
-2
-1
1
3
4
2
5
-2
-4
Roots
Vertex
Axis of Symmetry