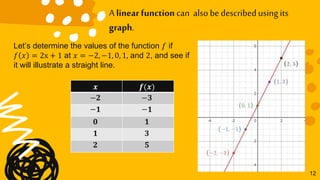
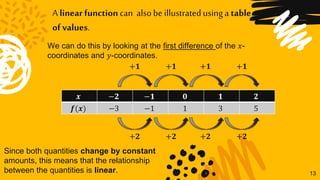
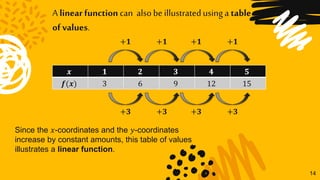
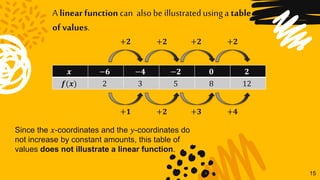
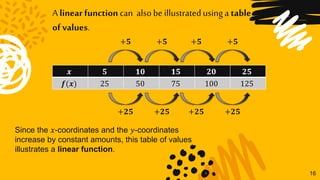
This document discusses linear functions and how to represent them using equations, graphs, and tables of values. It defines a linear function as one that can be written in the form f(x) = mx + b, where m is the slope and b is the y-intercept. Examples are provided to illustrate determining the slope and y-intercept from an equation and representing a linear function using an equation, table of values, or graph. It is explained that a linear function will produce a straight line on a graph and have constant differences in x- and y-coordinates in its table of values.

1. MATHEMATICS 8
Quarter 2 Week 4
Linear
Functions
MR. CARLO JUSTINO J. LUNA
MALABANIAS INTEGRATED SCHOOL
Angeles City

2. Learning Competency
2
✘ Graphs and illustrates a linear function and
its (a) domain; (b) range; (c) table of values;
(d) intercepts; and (e) slope (M8AL-IId-1)

3. Linear Function
A linear function is a function that can be written in the
form
𝒇 𝒙 = 𝒎𝒙 + 𝒃
✘ where 𝑚 and 𝑏 are real numbers
✘ where 𝑚 tells us the slope of a line and 𝑏 tells us
where the graph crosses the 𝑦-axis.
3

4. Linear Function
𝒇 𝒙 = 𝒎𝒙 + 𝒃
A linear function is a function whose graph is a straight
line. Its equation can be written in the form 𝒚 = 𝒎𝒙 +
𝒃, where 𝑥 and 𝑦 are used for the independent and
dependent variables, respectively, 𝑚 ≠ 0.
4

5. Linear Function
𝒇 𝒙 = 𝒎𝒙 + 𝒃
𝒚 = 𝒎𝒙 + 𝒃
𝒚 = 𝒇 𝒙
𝒈(𝒙) or 𝒉(𝒙)
5
✘ 𝑓(𝑥) means “the value of 𝑓 at 𝑥”
✘ letters other than 𝑓 such as 𝐺 and 𝐻, or 𝑔
and ℎ can also be used.

6. 6
Linear Functionas an Equation
Which of the following function is linear?
𝒚 = 𝒎𝒙 + 𝒃
𝒇 𝒙 = 𝒎𝒙 + 𝒃
1. 𝑦 = 8𝑥 − 5
2. 𝑦 = −
𝑥
3
+ 2
3. 𝑦 = 𝑥
4. 𝑦 =
2
𝑥
+ 7
5. 𝑦 = 𝑥2
− 3
Linear Function. It is in the form 𝑦 = 𝑚𝑥 + 𝑏, where 𝑚 = 8 and
𝑏 = −5
Linear Function. By rewriting the equation, we can have 𝑦 =
−
1
3
𝑥 + 2 where 𝑚 = −
1
3
and 𝑏 = 2.
Linear Function. By rewriting the equation, we can have 𝑦 =
𝑥 + 0 where 𝑚 = 1 and 𝑏 = 0.
Not a Linear Function. It cannot be expressed in the form 𝑦 =
𝑚𝑥 + 𝑏 because 𝑥 is in the denominator.
Not a Linear Function. The degree of the equation is on the
second degree.

7. 7
A linear function can alsobe describedusing its
graph.
Let’s determine the values of the function 𝑓 if 𝑓 𝑥 = 2x + 1 at 𝑥 =
− 2, −1, 0, 1, and 2, and see if it will illustrate a straight line.
SOLUTION:
1. 𝑓 𝑥 = 2𝑥 + 1
𝑓 −2 = 2 −2 + 1
𝑓 −2 = −4 + 1
𝒇 −𝟐 = −𝟑
Ordered pair: (−𝟐, −𝟑)
𝒙 𝒇(𝒙)
−𝟐 −𝟑
REMEMBER: Note that an ordered pair (𝑥, 𝑦) can be
written as (𝑥, 𝑓 𝑥 ) for any function in 𝑓 𝑥 notation.

8. 8
A linear function can alsobe describedusing its
graph.
Let’s determine the values of the function 𝑓 if 𝑓 𝑥 = 2x + 1 at 𝑥 =
− 2, −1, 0, 1, and 2, and see if it will illustrate a straight line.
SOLUTION:
2. 𝑓 𝑥 = 2𝑥 + 1
𝑓 −1 = 2 −1 + 1
𝑓 −1 = −2 + 1
𝒇 −𝟏 = −𝟏
Ordered pair: (−𝟏, −𝟏)
𝒙 𝒇(𝒙)
−𝟐 −𝟑
−𝟏 −𝟏

9. 9
A linear function can alsobe describedusing its
graph.
Let’s determine the values of the function 𝑓 if 𝑓 𝑥 = 2x + 1 at 𝑥 =
− 2, −1, 0, 1, and 2, and see if it will illustrate a straight line.
SOLUTION:
3. 𝑓 𝑥 = 2𝑥 + 1
𝑓 0 = 2 0 + 1
𝑓 0 = 0 + 1
𝒇 𝟎 = 𝟏
Ordered pair: (𝟎, 𝟏)
𝒙 𝒇(𝒙)
−𝟐 −𝟑
−𝟏 −𝟏
𝟎 𝟏

10. 10
A linear function can alsobe describedusing its
graph.
Let’s determine the values of the function 𝑓 if 𝑓 𝑥 = 2x + 1 at 𝑥 =
− 2, −1, 0, 1, and 2, and see if it will illustrate a straight line.
SOLUTION:
4. 𝑓 𝑥 = 2𝑥 + 1
𝑓 1 = 2 1 + 1
𝑓 1 = 2 + 1
𝒇 𝟏 = 𝟑
Ordered pair: (𝟏, 𝟑)
𝒙 𝒇(𝒙)
−𝟐 −𝟑
−𝟏 −𝟏
𝟎 𝟏
𝟏 𝟑

11. 11
A linear function can alsobe describedusing its
graph.
Let’s determine the values of the function 𝑓 if 𝑓 𝑥 = 2x + 1 at 𝑥 =
− 2, −1, 0, 1, and 2, and see if it will illustrate a straight line.
SOLUTION:
5. 𝑓 𝑥 = 2𝑥 + 1
𝑓 2 = 2 2 + 1
𝑓 2 = 4 + 1
𝒇 𝟐 = 𝟓
Ordered pair: (𝟐, 𝟓)
𝒙 𝒇(𝒙)
−𝟐 −𝟑
−𝟏 −𝟏
𝟎 𝟏
𝟏 𝟑
𝟐 𝟓

12. 12
A linear function can alsobe describedusing its
graph.
Let’s determine the values of the function 𝑓 if
𝑓 𝑥 = 2x + 1 at 𝑥 = −2, −1, 0, 1, and 2, and see if
it will illustrate a straight line.
𝒙 𝒇(𝒙)
−𝟐 −𝟑
−𝟏 −𝟏
𝟎 𝟏
𝟏 𝟑
𝟐 𝟓

13. 13
A linear function can alsobe illustratedusinga table
of values.
We can do this by looking at the first difference of the 𝑥-
coordinates and 𝑦-coordinates.
𝒙 −𝟐 −𝟏 𝟎 𝟏 𝟐
𝒇(𝒙) −3 −1 1 3 5
+𝟏 +𝟏 +𝟏 +𝟏
+𝟐 +𝟐 +𝟐 +𝟐
Since both quantities change by constant
amounts, this means that the relationship
between the quantities is linear.

14. 14
A linear function can alsobe illustratedusinga table
of values.
𝒙 𝟏 𝟐 𝟑 𝟒 𝟓
𝒇(𝒙) 3 6 9 12 15
+𝟏 +𝟏 +𝟏 +𝟏
+𝟑 +𝟑 +𝟑 +𝟑
Since the 𝑥-coordinates and the 𝑦-coordinates
increase by constant amounts, this table of values
illustrates a linear function.

15. 15
A linear function can alsobe illustratedusinga table
of values.
𝒙 −𝟔 −𝟒 −𝟐 𝟎 𝟐
𝒇(𝒙) 2 3 5 8 12
+𝟐 +𝟐 +𝟐 +𝟐
+𝟏 +𝟐 +𝟑 +𝟒
Since the 𝑥-coordinates and the 𝑦-coordinates do
not increase by constant amounts, this table of
values does not illustrate a linear function.

16. 16
A linear function can alsobe illustratedusinga table
of values.
𝒙 𝟓 𝟏𝟎 𝟏𝟓 𝟐𝟎 𝟐𝟓
𝒇(𝒙) 25 50 75 100 125
+𝟓 +𝟓 +𝟓 +𝟓
+𝟐𝟓 +𝟐𝟓 +𝟐𝟓 +𝟐𝟓
Since the 𝑥-coordinates and the 𝑦-coordinates
increase by constant amounts, this table of values
illustrates a linear function.

17. MATHEMATICS 8
Quarter 2 Week 4
Thank
you!
MR. CARLO JUSTINO J. LUNA
MALABANIAS INTEGRATED SCHOOL
Angeles City