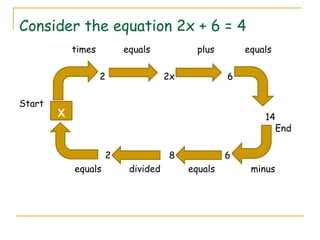
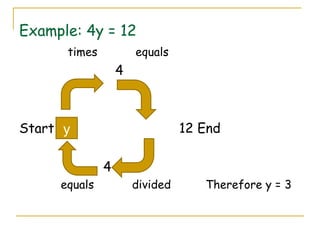
The document discusses linear equations and inequalities in one variable. It defines linear equations and inequalities, and describes methods for solving them including: guess-and-check, cover-up, and working backwards. It also covers properties of equality and inequality, and provides examples of solving linear equations and inequalities using these properties and graphical representations of solution sets on number lines.

1. LINEAR EQUATIONS and INEQUALITIES in ONE VARIABLE

2. Linear equations and Inequalities in One Variable Equation and Inequalities are relations between two quantities.

3. Equation is a mathematical sentence indicating that two expressions are equal. The symbol “=“ is used to indicate equality. Ex. 2x + 5 = 9 is a conditional equation since its truth or falsity depends on the value of x 2 + 9 = 11 is identity equation since both of its sides are identical to the same number 11.

4. Inequality is a mathematical sentence indicating that two expressions are not equal. The symbols <, >, are used to denote inequality. Ex. 3 + 2 ≠ 4 is an inequality If two expressions are unequal, then their relationship can be any of the following, >, ≥, < or ≤.

5. Linear equation in one variable is an equation which can be written in the form of ax + b = 0, where a and b are real-number constants and a ≠ 0. Ex. x + 7 = 12

6. Solution Set of a Linear Equation Example 4x + 2 = 10 this statement is either true of false If x = 1, then 4x + 2 = 10 is false because 4(1) + 2 is ≠ 10 If x = 2, then 4x + 2 = 10 is true because 4(2) + 2 = 10

7. B. x – 4 < 3 this statement is either true or false If x =6, then x – 4 is true because 6 – 4 < 3 If x = 10 , then x – 4 is false because 6 – 4 is not < 3 When a number replaces a variable in an equation (or inequality) to result in a true statement, that number is a solution of the equation (or inequality). The set of all solutions for a given equation (or inequality) as called the solution set of the equation (or inequality).

8. Solution Set of Simple Equations and Inequalities in One Variable by Inspection To solve an equation of inequality means to find its solution set. There are three(3) ways to solve an equation or inequality by inspection

9. A. Guess-and-Check In this method, one guesses and substitutes values into an equation of inequality to see if a true statement will result.

10. Consider the inequality x – 12 < 4 If x = 18, then 18 – 12 is not < 4 If x = 17, then 17 – 12 is not < 4 If x = 16, then 16 – 12 is not < 4 If x = 15, then 15 – 12 < 4 If x = 14, then 14 – 12 < 4 Inequality x - 12 < 4 is true for all values of x which are less than 16. Therefore, solution set of the given inequality is x < 16.

11. Another example X + 3 = 7 If x = 6, then 6 + 3 ≠ 7 If x = 5, then 5 + 3 ≠ 7 If x = 4, then 4 + 3 = 7 Therefore x = 4

12. B. Cover-up In this method , one covers up the term with the variable.

13. Example Consider equation x + 9 = 15 x + 9 = 15 + 9 = 15 To result in a true statement, the must be 6. Therefore x = 6

14. Another example X – 1 = 3 – 1 = 3 x = 4

15. C. Working Backwards In this method, the reverse procedure is used

16. Consider the equation 2x + 6 = 4 times equals plus equals 2 2x 6 Start 14 End 2 8 6 equals divided equals minus x

17. Example: 4y = 12 times equals 4 Start 12 End 4 equals divided Therefore y = 3 y

18. Properties of Equality and Inequality

19. Properties of Equality Let a, b, and c be real numbers. Reflexive Property a = a Ex. 3 = 3, 7 = 7 or 10.5 = 10.5

20. B. Symmetric Property If a = b, then b = a Ex. If 3 + 5 = 8, then 8 = 3 + 5 If 15 = 6 + 9, then 6 + 9 = 15 If 20 = (4)(5), then (4)(5) = 20

21. C. Transitive Property If a = b and b = c, then a = c Ex. If 8 + 5 = 13 and 13 = 6 + 7 then 8 + 5 = 6 + 7 If (8)(5) = 40 and 40 = (4)(10) then (8)(5) = (4)(10)

22. D. Addition Property If a = b, then a + c = b + c Ex. If 3 + 5 = 8, then (3 + 5) = 3 = 8 +3

23. E. Subtraction Property If a = b, then a – c = b – c Ex. 3 + 5 = 8, then (3 + 5) – 3 = 8 - 3

24. F. Multiplication Property If a = b, then ac = bc Ex. (4)(6) = 24, then (4)(6)(3) = (24)(3)

25. G. Division Property If a = b, and c ≠ 0, then a/c = b/c Ex. If (4)(6) = 24, then (4)(6)/3 = 24/3

26. Properties of Inequality Let a, b and c be real numbers. Note: The properties of inequalities will still hold true using the relation symbol ≤ and ≥.

27. A. Addition Property If a < b, then a + c < b + c Ex. If 2 < 3, then 2 + 1 < 3 + 1

28. B. Subtraction Property If a < b, then a – c < b – c Ex. If 2 < 3, then 2 – 1 < 3 – 1

29. C. Multiplication Property If a < b and c > 0, then ac < bc IF a < b and c < 0, then ac > bc Ex. If 2 < 3, then (2)(2) < (3)(2) If 2 < 3, then (2)(-2) > (3)(-2)

30. D. Division Property If a < b and c > 0, then a/c < b/c If a < b and c < 0, then a/c > b/c Ex. If 2 < 3, then 2/3 < 3/3 If 2 < 3, then 2/-3 > 3/-3

31. Solving Linear Equations in One Variable

32. Example: Solve the following equations: x – 5 = 8 x – 5 + 5 = 8 + 5 add 5 to both sides x + 0 = 13 of the equation x = 13 Recall that if the same number is added to both sides of the equation, the resulting sums are equal.

33. x – 12 = -18 x – 12 + 12 = -18 + 12 add 12 to both sides x + 0 = -6 x = -6 This problem also uses the addition property of equalities.

34. x + 4 = 6 x + 4 – 4 = 6 – 4 subtract 4 to both sides of x + 0 = 2 the equation x = 2 Recall that if the same number is subtracted to both sides of the equation, the differences are equal.

35. x + 12 = 25 x + 12 – 12 = 25 – 12 subtract 12 to both x + 0 = 25 – 12 sides This problem also uses the subtraction property of equalities.

36. x/2 = 3 x/2 . 2 = 3 . 2 multiply both sides by 2 x = 6 Recall that if the same number is multiplied to both sides of the equation, the products are equal.

37. 6. x/7 = -5 x/7 . 7 = -5 .7 multiply both sides by 7 x = -35 This problem also uses multiplication property of equalities.

38. 7. 5 x = 35 5x/5 = 35/5 both sides of the equation is X = 7 divided by the numerical coefficient of x to make the coefficient of x equals to 1 Recall the if both sides of the equation is divided by a non-zero number, the quotients are equal.

39. 8. 12y = -72 12y/12 = -72/12 divide both sides by 12 y = -6 This problem also uses the division property of equalities.

40. Other equations in one variable are solved using more than on property of equalities. 9. 2x + 3 = 9 2x+ 3 – 3 = 9 – 3 subtraction property 2x = 6 2x/2 = 6/2 division property x = 3

41. 10. 5y – 4 = 12 – y 5y – 4 + 4 = 12 – y + 4 addition property 5y = 16 – y 5y + y = 16 – y + y addition property 6y = 16 6y/5 = 16/5 division property y = 2 4/6

42. Solving Linear Inequalities in One Variable

43. The solution set o inequalities maybe represented on a number line. Recall that a solution of a linear inequality in one variable is a real number which makes the inequality true. Example: 1. Graph x > 6 on a number line O x>6 0 1 2 3 4 5 6 7 8 9 10 11 The ray indicates the solution set of x > 6

44. The ray indicates the that he solution set, x > 6 consist of all numbers greater than 6. The open circle of 6 indicates that 6 is not included.

45. 2. Graph the solution set x ≤ -1 on a number line. x ≤ -1 -2 -1 0 1 The ray indicates that the solution set of x ≤ -1 consist of all the numbers less than or equal to -1. The solid circle of -1 indicates that -1 is included in the solution set.

46. Applying the Properties of Inequalities in Solving Linear Inequalities: 1. Solve x – 2 > 6 and graph the solution set. x – 2 > 6 x – 2 + 2 > 6 + 2 add 2 to both sides of the x + 0 > 8 inequality x > 8 O x > 8 8

47. 2. x + 15 < -7 x + 15 – 15 < -7 – 15 subtract 15 from both sides of the x +0 < - 22 inequalities. x < -22 x < -22 o -22

48. Solving Word Problems Involving Linear Equations

49. Steps in solving word problems: Read and understand the problem. Identify what is given and what is unknown. Choose a variable to represent the unknown number. Express the other unknown, if there are any., in terms of the variable chosen in step 1. Write a equation to represent the relationship among the given and unknown/s. Solve the equation for the unknown and use the solution to find for the quantities being asked. Check by going back to the original statement.

50. Example: One number is 3 less than another number. If their sum is 49, find the two numbers. Step 1: Let x be the first number. Step 2: Let x – 3 be the second number. Step 3: x + ( x – 3) = 49 Step 4: x + x – 3 = 49 2x – 3 = 49 2x = 49 + 3 2x = 52 x = 26 the first number x – 3 = 23 the second number Step 5: Check: The sum of 26 and 23 is 49, and 23 is 3 less than 26.

51. 2. Six years ago, Mrs. dela Rosa was 5 times as old as her daughter Leila. How old is Leila now if her age is one-third of her mother’s present age? Solution: Step 1: Let x be Leila’s age now 3x is Mrs. dela Rosa’s age now Step 2: x – 6 is Leila’s age 6 years ago 3x – 6 is Mrs. dela Rosa’s age 6 years ago Step 3: 5(x – 6) = 3x – 6 Step 4: 5(x – 6) = 3x – 6 5x – 30 = 3x – 6 5x – 30 + 30 = 3x – 6 + 30 5x = 3x + 24 5x – 3x = 3x +24 – 3x 2x = 24 2x/2 = 24/ 2 X = 12 Leila’s age now 3x = 36 Mrs. dela Rosa’s age now Step 5: Check: Thrice of Leila’s present age, 12, is Mrs. dela Rosa’s presnt age, 36. Six years ago, Mrs. dela Rosa was 36 – 6 = 30years old which was five times Leila’s age, 12 – 6 = 6.