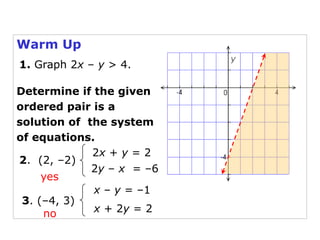
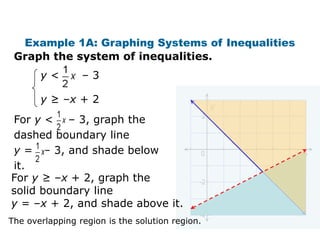
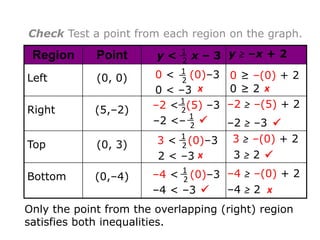
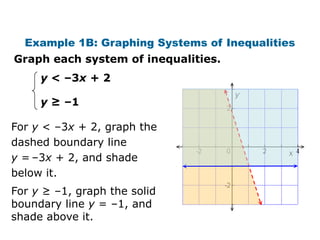
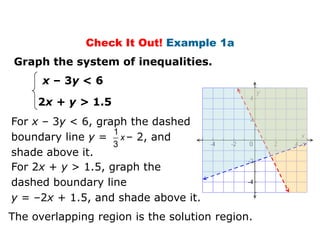
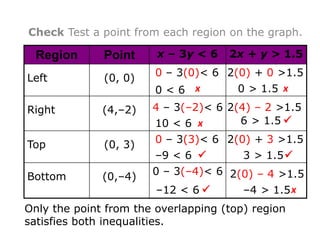
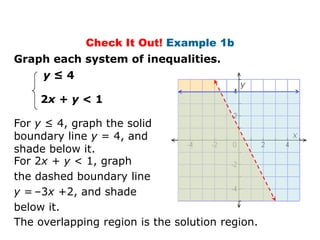
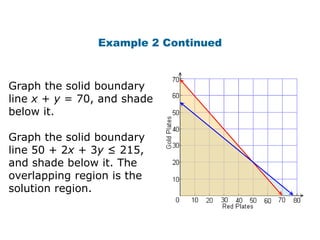
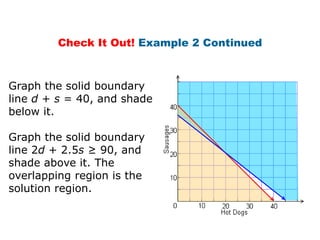
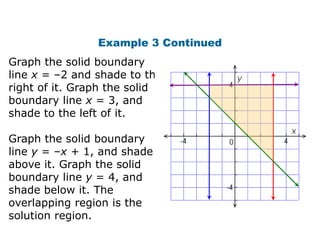
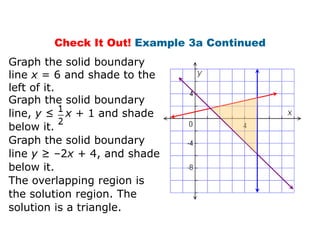
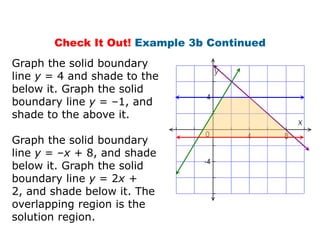
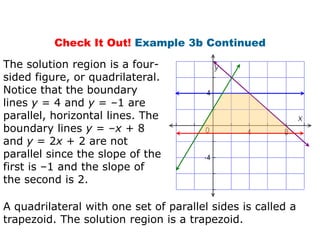
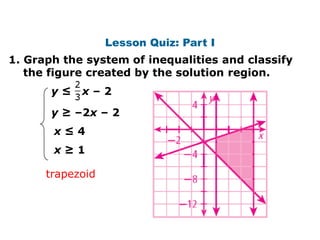
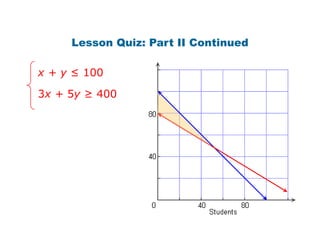
Here is the system of inequalities for the cross-country team problem: Let x = number of water bottles sold to students Let y = number of water bottles sold to others x + y ≤ 100 (they have 100 bottles total) 3x + 5y ≥ 400 (they need at least $400) Graph the regions defined by these inequalities and the overlapping region is the solution.

1. Solving Systems of Linear Inequalities
Warm Up
Lesson Presentation
Lesson Quiz

2. Warm Up
1. Graph 2x – y > 4.
Determine if the given
ordered pair is a
solution of the system
of equations.
2x + y = 2
2. (2, –2)
2y – x = –6
yes
x – y = –1
3. (–4, 3)
no x + 2y = 2

3. Objective
Solve systems of linear inequalities.

4. Vocabulary
system of linear inequalities

5. When a problem uses phrases like “greater than”
or “no more than,” you can model the situation
using a system of linear inequalities.
A system of linear inequalities is a set of two or
more linear inequalities with the same variables.
The solution to a system of inequalities is often an
infinite set of points that can be represented
graphically by shading.
When you graph multiple inequalities on the same
graph, the region where the shadings overlap is the
solution region.

6. Example 1A: Graphing Systems of Inequalities
Graph the system of inequalities.
y< –3
y ≥ –x + 2
For y < – 3, graph the
dashed boundary line
y = – 3, and shade below
it.
For y ≥ –x + 2, graph the
solid boundary line
y = –x + 2, and shade above it.
The overlapping region is the solution region.

7. Check Test a point from each region on the graph.
Region Point y< 1 x–3 y ≥ –x + 2
2
Left (0, 0) 0 < 1 (0)–3
2 0 ≥ –(0) + 2
0 < –3 x 0≥2 x
Right (5,–2) –2 < 1 (5) –3
2
–2 ≥ –(5) + 2
–2 <– 1 
2 –2 ≥ –3 
Top (0, 3) 3 < 1 (0)–3 3 ≥ –(0) + 2
2
2 < –3 x 3≥2 
Bottom (0,–4) –4 < 1 (0)–3 –4 ≥ –(0) + 2
2
–4 < –3  –4 ≥ 2 x
Only the point from the overlapping (right) region
satisfies both inequalities.

8. Helpful Hint
If you are unsure which direction to shade, use
the origin as a test point.

9. Example 1B: Graphing Systems of Inequalities
Graph each system of inequalities.
y < –3x + 2
y ≥ –1
For y < –3x + 2, graph the
dashed boundary line
y = –3x + 2, and shade
below it.
For y ≥ –1, graph the solid
boundary line y = –1, and
shade above it.

10. Example 1B Continued
Check Choose a point in the solution region,
such as (0, 0), and test it in both inequalities.
y < –3x + 2 y ≥ –1
0 < –3(0) + 2 0 ≥ –1
0<2  0 ≥ –1 
The test point satisfies both inequalities, so the
solution region is correct.

11. Check It Out! Example 1a
Graph the system of inequalities.
x – 3y < 6
2x + y > 1.5
For x – 3y < 6, graph the dashed
1
boundary line y = x – 2, and
3
shade above it.
For 2x + y > 1.5, graph the
dashed boundary line
y = –2x + 1.5, and shade above it.
The overlapping region is the solution region.

12. Check Test a point from each region on the graph.
Region Point x – 3y < 6 2x + y > 1.5
0 – 3(0)< 6 2(0) + 0 >1.5
Left (0, 0)
0<6 x 0 > 1.5 x
Right (4,–2) 4 – 3(–2)< 6 2(4) – 2 >1.5
10 < 6 x 6 > 1.5 
Top (0, 3) 0 – 3(3)< 6 2(0) + 3 >1.5
–9 < 6  3 > 1.5 
Bottom (0,–4) 0 – 3(–4)< 6 2(0) – 4 >1.5
–12 < 6  –4 > 1.5 x
Only the point from the overlapping (top) region
satisfies both inequalities.

13. Check It Out! Example 1b
Graph each system of inequalities.
y≤4
2x + y < 1
For y ≤ 4, graph the solid
boundary line y = 4, and
shade below it.
For 2x + y < 1, graph
the dashed boundary line
y = –3x +2, and shade
below it.
The overlapping region is the solution region.

14. Check It Out! Example 1b Continued
Check Choose a point in the solution region,
such as (0, 0), and test it in both directions.
y≤4 2x + y < 1
0≤4 2(0) + 0 < 1
0≤4  0<1 
The test point satisfies both inequalities, so the
solution region is correct.

15. Example 2: Art Application
Lauren wants to paint no more than 70
plates for the art show. It costs her at least
$50 plus $2 per item to produce red plates
and $3 per item to produce gold plates. She
wants to spend no more than $215. Write
and graph a system of inequalities that can
be used to determine the number of each
plate that Lauren can make.

16. Example 2 Continued
Let x represent the number of red plates, and let
y represent the number of gold plates.
The total number of plates Lauren is willing to paint
can be modeled by the inequality x + y ≤ 70.
The amount of money that Lauren is willing to
spend can be modeled by 50 + 2x + 3y ≤ 215.
x 0
The system of inequalities is y 0 .
x + y ≤ 70
50 + 2x + 3y ≤ 215

17. Example 2 Continued
Graph the solid boundary
line x + y = 70, and shade
below it.
Graph the solid boundary
line 50 + 2x + 3y ≤ 215,
and shade below it. The
overlapping region is the
solution region.

18. Example 2 Continued
Check Test the point (20, 20) in both inequalities.
This point represents painting 20 red and 20 gold
plates.
x + y ≤ 70 50 + 2x + 3y ≤ 215
20 + 20 ≤ 70 50 + 2(20) + 3(20) ≤ 215
40 ≤ 70  150 ≤ 215 

19. Check It Out! Example 2
Leyla is selling hot dogs and spicy sausages at
the fair. She has only 40 buns, so she can sell
no more than a total of 40 hot dogs and spicy
sausages. Each hot dog sells for $2, and each
sausage sells for $2.50. Leyla needs at least
$90 in sales to meet her goal. Write and graph
a system of inequalities that models this
situation.

20. Check It Out! Example 2 Continued
Let d represent the number of hot dogs, and let s
represent the number of sausages.
The total number of buns Leyla has can be modeled
by the inequality d + s ≤ 40.
The amount of money that Leyla needs to meet
her goal can be modeled by 2d + 2.5s ≥ 90.
d 0
s 0
The system of inequalities is .
d + s ≤ 40
2d + 2.5s ≥ 90

21. Check It Out! Example 2 Continued
Graph the solid boundary
line d + s = 40, and shade
below it.
Graph the solid boundary
line 2d + 2.5s ≥ 90, and
shade above it. The
overlapping region is the
solution region.

22. Check It Out! Example 2 Continued
Check Test the point (5, 32) in both inequalities.
This point represents selling 5 hot dogs and 32
sausages.
d + s ≤ 40 2d + 2.5s ≥ 90
5 + 32 ≤ 40 2(5) + 2.5(32) ≥ 90
37 ≤ 40  90 ≥ 90 

23. Systems of inequalities may contain more
than two inequalities.

24. Example 3: Geometry Application
Graph the system of inequalities, and classify
the figure created by the solution region.
x ≥ –2
x≤3
y ≥ –x + 1
y≤4

25. Example 3 Continued
Graph the solid boundary
line x = –2 and shade to the
right of it. Graph the solid
boundary line x = 3, and
shade to the left of it.
Graph the solid boundary
line y = –x + 1, and shade
above it. Graph the solid
boundary line y = 4, and
shade below it. The
overlapping region is the
solution region.

26. Check It Out! Example 3a
Graph the system of inequalities, and classify
the figure created by the solution region.
x≤6
y≤ x+1
y ≥ –2x + 4

27. Check It Out! Example 3a Continued
Graph the solid boundary
line x = 6 and shade to the
left of it.
Graph the solid boundary
line, y ≤ x + 1 and shade
below it.
Graph the solid boundary
line y ≥ –2x + 4, and shade
below it.
The overlapping region is
the solution region. The
solution is a triangle.

28. Check It Out! Example 3b
Graph the system of inequalities, and classify
the figure created by the solution region.
y≤4
y ≥–1
y ≤ –x + 8
y ≤ 2x + 2

29. Check It Out! Example 3b Continued
Graph the solid boundary
line y = 4 and shade to the
below it. Graph the solid
boundary line y = –1, and
shade to the above it.
Graph the solid boundary
line y = –x + 8, and shade
below it. Graph the solid
boundary line y = 2x +
2, and shade below it. The
overlapping region is the
solution region.

30. Check It Out! Example 3b Continued
The solution region is a four-
sided figure, or quadrilateral.
Notice that the boundary
lines y = 4 and y = –1 are
parallel, horizontal lines. The
boundary lines y = –x + 8
and y = 2x + 2 are not
parallel since the slope of the
first is –1 and the slope of
the second is 2.
A quadrilateral with one set of parallel sides is called a
trapezoid. The solution region is a trapezoid.

31. Lesson Quiz: Part I
1. Graph the system of inequalities and classify
the figure created by the solution region.
y≤ x–2
y ≥ –2x – 2
x≤4
x≥1
trapezoid

32. Lesson Quiz: Part II
2. The cross-country team is selling water
bottles to raise money for the team. The
price of the water bottle is $3 for students
and $5 for everyone else. The team needs
to raise at least $400 and has 100 water
bottles. Write and graph a system of
inequalities that can be used to determine
when the team will meet its goal.

33. Lesson Quiz: Part II Continued
x + y ≤ 100
3x + 5y ≥ 400