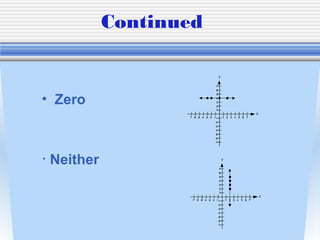
This document defines slope and provides examples for teaching students about slope. It explains that slope is the ratio of vertical to horizontal change and can be positive, negative, zero, or undefined. The objectives are for students to identify slope from graphs, calculate slope using rise over run, and apply the slope formula to find slope given two points. Examples are provided to demonstrate calculating slope from graphs and points using rise over run and the slope formula.

1. Meaning of Slope
Sima Javaheri
&
Sara Kelly

2. California Content Standard
• 3.3 Graph linear functions, noting that the
vertical change (change in y- value) per
unit of horizontal change (change in x-
value) is always the same and know that
the ratio ("rise over run") is called the
slope of a graph.

3. NCTM Standard
• Represent, analyze, and generalize a
variety of patterns with tables, graphs,
words, and, when possible, symbolic rules

4. Objectives of the Lesson
• Given a graph of a line, students will be
able to identify the slope as being positive,
negative, zero, or neither.
• Given a graph of a line, students will be
able to calculate slope by using rise over
run.
• Given a two points on a line, students will
be able to apply the slope formula
accurately.

5. What is Slope???
Slope is the ratio of the vertical change to the
horizontal change. In a linear relationship, it is
a constant rate of change. It can also be
characterized as the steepness of a line.
vertical change rise y2 − y1
slope = m = = =
horizontal change run x2 − x1

7. Positive vs. Negative Slopes
• A line that moves upward from left to right
has a positive slope.
Hint: If you can transform the line to resemble a
“P” then it is positive!
• A line that moves downward from left to
right has a negative slope.
Hint: If you can transform the line to resemble a
“N” then it is negative!

8. Kinds of Slopes
• Positive Slope
• Ne gative S lope

9. Zero and Neither Slope
A line that is flat from left to right has a
zero slope.
A line that is straight up and down (vertical)
has no s lope (neither).

10. Continued
• Zero
• Neither

11. Rise over Run
rise
Slope =
run
Rise is the vertical distance between the points
Run is the horizontal distance between the
points

12. Use Rise over Run
•What is the rise
value? Rise = 4
•What is the run
value? Run = 1
What is the
Slope?
rise 4
= =4
run 1

13. Slope Formula
• Given two points ( x1 , y1 ) and ( x2 , y2 ) , the
slope can be calculated by substituting the x-
and y-values into the following formula:
y 2 −y1
m=
x2 −x1

14. Example
Find the slope of the line that goes
through these two points (1, 1) and (2,3):
3 −1 2
m= = =2
2 −1 1

15. Now, you try…
Given (0,4) and (2, -2), compute
the slope using the slope formula:
−2 −4 −6
m= = = −3
2 −0 2

16. References
1. Kaplan, Andrew. Math On Call. Wilmington:
Houghton Mifflin, 1998.
1. Van de Walle, J, & Lovin, L, Teaching Student
Centered Mathematics, Boston: Pearson (2001).
2. http://www.math.iupui.edu/~momran/m119/notes/slope