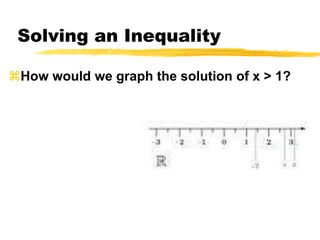
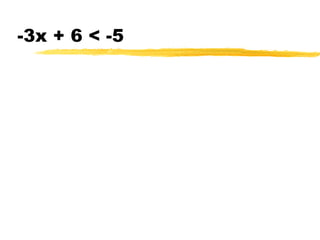
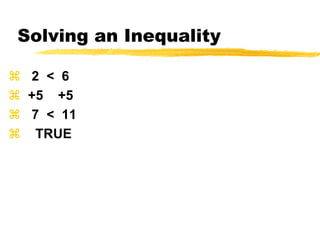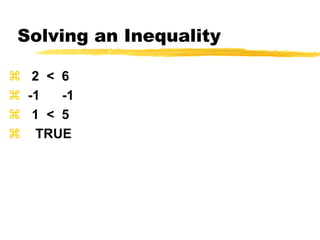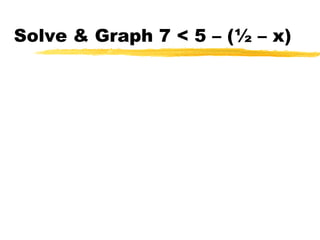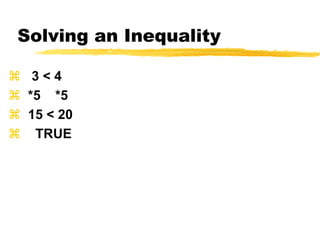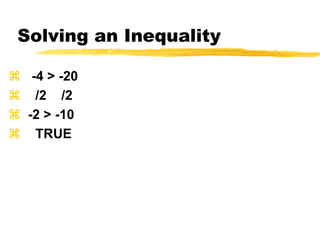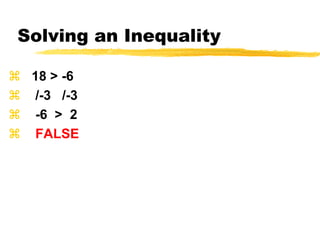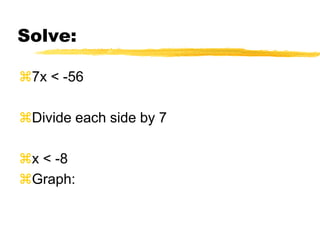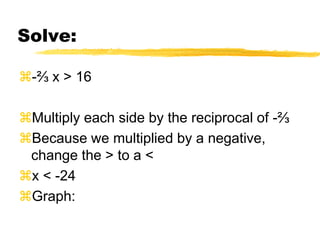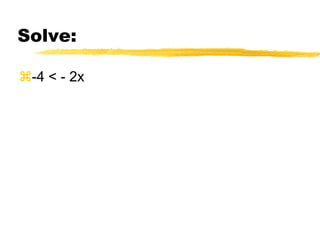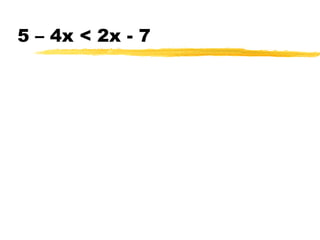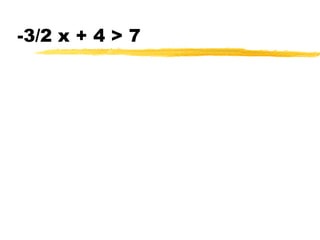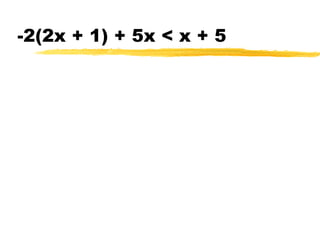This document discusses solving and graphing inequalities using addition, subtraction, multiplication, and division properties. It defines inequalities and their solution sets. Key points covered include: adding or subtracting the same number to both sides of an inequality produces an equivalent inequality; multiplying or dividing both sides by a positive number also produces equivalence, while a negative number requires reversing the inequality sign; and several worked examples are provided to illustrate solving and graphing various inequalities.

1. 5.1 Addition and Subtraction Problems of InequalityObjective: To solve and graph the solution set of an inequality by using the Addition or Subtraction Property of InequalityFrameworks: 10.P.1, 10.P.7

2. How do you read . . .a < b a is less than ba > b a is greater than b

3. InequalityThe open sentence x < -2 is an example of an inequalityAn inequality contains at least one variable and consists of 2 expressions with an inequality symbol such as <, >, or ≠ between them.

4. Solving an InequalityTo solve an inequality means to find a solution set.What is the solution set of x < -2?On a number line:open circle meansnot including this point

5. Solving an InequalityHow would we graph the solution of x > 1?

6. Solving an InequalityThe Addition and Subtraction Properties of Equality allow you to add or subtract the same number from each side of an equation to obtain an equivalent equation.x – 4 = 3 x + 2 = 5 Do inequalities work the same way?

7. Solving an Inequality 2 < 6 +5 +5 7 < 11 TRUE

8. Solving an Inequality 2 < 6 -1 -1 1 < 5 TRUE

9. Equivalent InequalitiesOpen inequalities with the same solution set are called equivalent inequalities.

10. Addition Property of InequalityFor all real numbers a, b, and c, if a < b, then a + c < b + c, and if a > b, then a + c > b + cIn other words, adding the same number to each side of an equality produces an equivalent equality.

11. Subtraction Property of InequalityFor all real numbers a, b, and c, if a < b, then a - c < b - c, and if a > b, then a - c > b - cIn other words, subtracting the same number from each side of an equality produces an equivalent equality.

12. Solve x – 8 > -11 & Graph

13. Solve & Graph 7 < 5 – (½ – x)

14. After Mary paid $8.36 for a snack she had less than $2.50 left. How much money did she have originally?

15. After Bill paid $7.21 at the movies, he had less than $1.75 left. How much money did he have originally?

16. 5.2 Multiplication & Division Problems of InequalityObjective: To solve and graph the solution set of an inequality by using the Multiplication or Division Property of InequalityFrameworks: 10.P.1, 10.P.7

17. Solving an InequalityThe Multiplication and Division Properties of Equality allow you to add or subtract the same number from each side of an equation to obtain an equivalent equation.x / 4 = 2 x * 3 = 21Do inequalities work the same way?

18. Solving an Inequality 3 < 4 *5 *5 15 < 20 TRUE

19. Solving an Inequality -4 > -20 /2 /2 -2 > -10 TRUE

20. Solving an Inequality -5 < -3 *-1 *-1 5 < 3FALSE

21. Solving an Inequality 18 > -6 /-3 /-3 -6 > 2FALSE

22. Notice:Multiplying or Dividing each side of a true equality by a negative number produces a false inequality

23. Multiplication Property of Inequality, Part 1For all real numbers a, b, and c,if a < b and c > 0, then ac < bc, andif a > b and c > 0, then ac > bcThat is, multiplying each side of an inequality by the same positive number produces an equivalent inequality.

24. Multiplication Property of Inequality, Part 2For all real numbers a, b, and c,if a < b and c < 0, then ac > bc, andif a > b and c < 0, then ac < bcThat is, multiplying each side of an inequality by the same negative number and reversing the order of the inequality produces an equivalent inequality.

25. Division Property of Inequality, Part 1For all real numbers a, b, and c,if a < b and c > 0, then a/c < b/c, andif a > b and c > 0, then a/c > b/cThat is, dividing each side of an inequality by the same positive number produces an equivalent inequality.

26. Division Property of Inequality, Part 2For all real numbers a, b, and c,if a < b and c < 0, then ac > b/c, andif a > b and c < 0, then ac < b/cThat is, dividing each side of an inequality by the same negative number and reversing the order of the inequality produces an equivalent inequality.

27. Solve:7x < -56Divide each side by 7x < -8Graph:

28. Solve:-⅔ x > 16Multiply each side by the reciprocal of -⅔ Because we multiplied by a negative, change the > to a <x < -24Graph:

29. Solve:-4 < - 2x

30. If Jill sells more than $100 worth of peanut brittle, she will win a radio. Each box of peanut brittle sells for $2.75. How many boxes must she sell to win the radio?2.75p > 100p > 100/2.75p > 36.3636Can she sell 36.36 boxes?Jill must sell 37 boxes.

31. -3x + 6 < -5

32. 5 – 4x < 2x - 7

33. -3/2 x + 4 > 7

34. -2(2x + 1) + 5x < x + 5

35. Turn to p. 168Do 1 -14Turn to p. 169Do 16-19Turn to p. 173Do 1-9Turn to p. 174Do 27-30