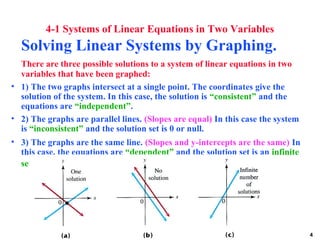
The document discusses methods for solving systems of linear equations in two variables, including graphing, elimination, and substitution. It provides examples of using each method to solve systems and determine if they have one solution, no solution, or infinitely many solutions. Key points covered are the three possible outcomes when graphing systems, the steps for the elimination and substitution methods, and how to determine the solution set.



![6
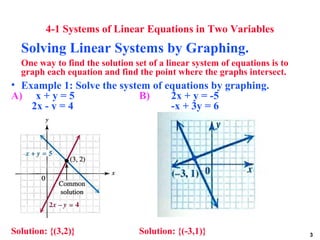
4-1 Systems of Linear Equations in Two Variables
Solving Linear Systems of two variables by
Method of Elimination.
• Example 2: Solve the system : 2x + 3y = 19
Step 1: Both equations are in standard form 3x - 7y = -6
Step 2: Choose the variable x to eliminate: Multiply the top equation by 3, the bottom
equation by -2
3[2x + 3y = 19] 6x + 9y = 57
-2[3x - 7y = -6] -6x +14y = 12
Step 3: Add the new equations to eliminate a variable
0x + 23y = 69
Step 4: Solve the equation formed in step y = 3
Step 5: Substitute the result of Step 4 into either of the original equations and solve for the
other value. 2x + 3(3) = 19
2x = 10
x = 5 Solution Set: {(5,3)}
Step 6: Check the solution and write the solution set.](https://image.slidesharecdn.com/systemsoflinearequations-150115090839-conversion-gate02/85/Systems-of-linear-equations-6-320.jpg)
![7
4-1 Systems of Linear Equations in Two Variables
Solving Linear Systems of two variables by
Method of Elimination.
• Example 3:
Solve the system :
2[2x - 3y = 1] 4x - 6y = 2
-3[3x - 2y = 9] -9x + 6y = -27
-5x + 0y = -25
x = 5 3(5) - 2y = 9
-2y = -6
Solution Set: {(5,3)} y = 3
1 1 1
rewrite as 6[ ] 2 3 1
3 2 6
: 2 3 1
1 1 1
3 2 6
3 2 9
3 2 9
x y x y
Solv
x y
x y
e x y
x y
⇒ − = ⇒ − =
− =
−
− =
=
=
−](https://image.slidesharecdn.com/systemsoflinearequations-150115090839-conversion-gate02/85/Systems-of-linear-equations-7-320.jpg)
![8
4-1 Systems of Linear Equations in Two Variables
Solving Linear Systems of two variables by
Method of Elimination.
• Example 4:
Solve the system : 2x + y = 6
-8x - 4y = -24
4[2x + y = 6] 8x + 4y = 24
-8x -4y = -24 -8x - 4y = -24
0 = 0 True
Solution Set: {(x,y)| 2x + y = 6}
Note: When a system has dependent equations and an infinite number
of solutions, either equation can be used to produce the solution set.
Answer is given in set-builder notation.](https://image.slidesharecdn.com/systemsoflinearequations-150115090839-conversion-gate02/85/Systems-of-linear-equations-8-320.jpg)
![9
4-1 Systems of Linear Equations in Two Variables
Solving Linear Systems of two variables
by Method of Elimination.
• Example 5:
Solve the system : 4x - 3y = 8
8x - 6y = 14
-2[4x - 3y = 8] -8x + 6y = -16
8x - 6y = 14 8x - 6y = 24
0 = 8 False
Solution Set: 0 or null
Note: There are no ordered pairs that satisfy both
equations. The lines are parallel. There is no solution.](https://image.slidesharecdn.com/systemsoflinearequations-150115090839-conversion-gate02/85/Systems-of-linear-equations-9-320.jpg)


![12
4-1 Systems of Linear Equations in Two Variables
Solving Linear Systems of two variables by
Method of Substitution.
• Example 7:
Solve the system :
y = -2x + 2
-2x + 5(-2x + 2) = 22 -2x - 10x + 10 = 22
-12x = 12
x = -1 2(-1) + y = 2
y = 4
Solution Set: {(-1,4)}
1 1 1
2 4 2
2
1 1 1
rewrite as 4[ ] 2 2
2 4 2
: 2 2
-2 5 2
5 2
2
2
x y
x y
x y x y
Solve x y
x y
⇒ + = ⇒ + =
+
+
=
+
=
=
=
+
−](https://image.slidesharecdn.com/systemsoflinearequations-150115090839-conversion-gate02/85/Systems-of-linear-equations-12-320.jpg)