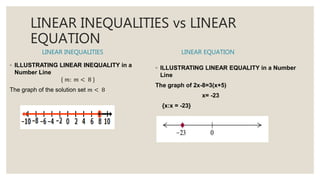
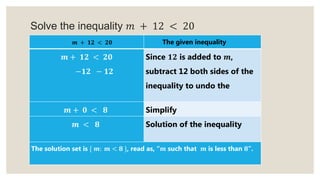
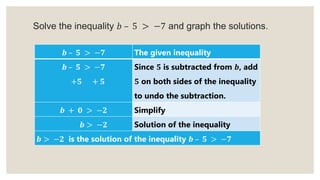
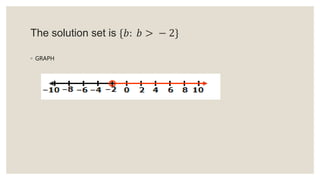
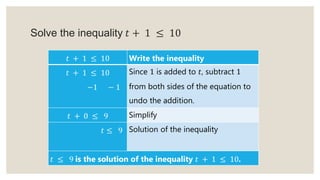
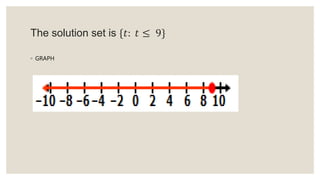
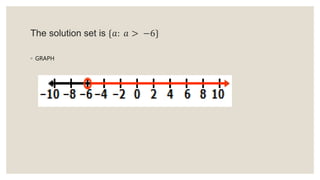
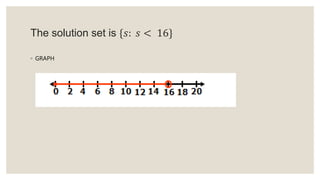
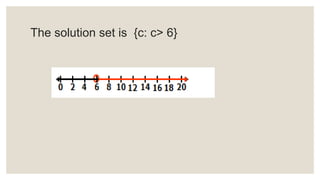
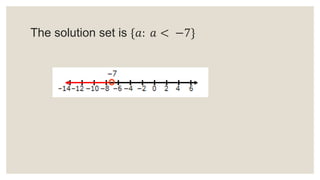
This document provides an overview of linear inequalities and equations for a mathematics class. It defines key terms like linear inequality, solution set, and graphs examples of solving different types of linear inequalities. Students are asked to solve sample inequalities, write the solution sets using set notation, and graph the solutions. The document compares linear inequalities and equations, and covers various properties for solving inequalities, including addition/subtraction, multiplication/division, and dealing with negative numbers.

1. WELCOME
TO
MATHEMATICS 7
CLASS
QUARTER 3
WEEK 2

2. At the end of the
lesson, you must
be able to:
Differentiate algebraic expression,
equation and inequalities
Finds the Solution of a Linear
inequality in one variable

3. LINEAR INEQUALITIES
AND LINEAR EQUATION

4. LINEAR INEQUALITIES vs LINEAR
EQUATION
LINEAR INEQUALITIES
is an algebraic expression related by
< “is less than,”
≤ “is less than or equal to,”
> “is greater than,” or
≥ “is greater than or equal
to.”
LINEAR EQUATION
is an algebraic expression related by
= “ is equal to”

5. LINEAR INEQUALITIES vs LINEAR
EQUATION
LINEAR INEQUALITIES
is a statement that shows two
numbers or expressions that are
not equal.
Example: 𝟓 > 𝟑
𝟐𝒙 ≤ −𝟔
LINEAR EQUATION
◦ is a statement that shows two
numbers or expressions that are
equal.
◦ Example: x – 2 = 8
2y + 3 = 5

6. LINEAR INEQUALITIES vs LINEAR
EQUATION
LINEAR INEQUALITIES
Solution of an inequality
◦ is a value of the variable that makes the
inequality true.
◦ Example: 𝑥 ≤ −3is a solution to the
inequality 2𝑥 ≤ −6
LINEAR EQUATION
Solution of an equality
◦ Is a value of a variable that makes the
equation true.
◦ Example: x = 2 is a solution of
2x = 4, because if we substitute 2 in the
equation 2x = 4 then, 2(2) = 4 which is
◦ 4 = 4 (true)

7. LINEAR INEQUALITIES vs LINEAR
EQUATION
LINEAR INEQUALITIES
Solution set
◦ is the set of all solutions
◦ Example: {−3, −4, −5, −6, −7, … } this set
is a solution set of
2𝑥 ≤ −6
x ≤ −3
◦ If all negative integers x ≤ −3
Is written inside the braces, then it is called
a solution set.
LINEAR EQUATION
Solution set
◦ is the set of all solutions. Finding the
solutions of an equation is also called
solving the equation.
◦ Example: {2} is a solution set of 2x = 4
◦ If x = 2 is written inside the braces, then it
is called a solution set.

8. LINEAR INEQUALITIES vs LINEAR
EQUATION
LINEAR INEQUALITIES
Solution set
◦ is the set of all solutions
◦ Example: {−3, −4, −5, −6, −7, … } this set is a
solution set of 2𝑥 ≤ −6
x ≤ −3
◦ If all negative integers x ≤ −3
Is written inside the braces, then it is called a
solution set.
◦ written in set notation using braces, { }. Solutions
may be given in set notation, or they may be
given in the form x = a certain real number
◦ {𝑥: 𝑥 ≤ −3}
LINEAR EQUATION
Solution set
◦ is the set of all solutions. Finding the solutions of an
equation is also called solving the equation.
◦ Example: {2} is a solution set of 2x = 4
◦ If x = 2 is written inside the braces, then it is called
a solution set.
◦ are written in set notation using braces, { }.
Solutions may be given in set notation, or they may
be given in the form x = n, where n is a real
number.
◦ {xIx = 2}

9. LINEAR INEQUALITIES vs LINEAR
EQUATION
LINEAR INEQUALITIES
◦ ILLUSTRATING LINEAR INEQUALITY in a
Number Line
{ 𝑚: 𝑚 < 8 }
The graph of the solution set 𝑚 < 8
LINEAR EQUATION
◦ ILLUSTRATING LINEAR EQUALITY in a Number
Line
The graph of 2x-8=3(x+5)
x= -23
{x:x = -23}

10. SOLVING LINEAR
INEQUALITIES

11. Addition and Subtraction Properties of Inequality
Addition Property of Inequality: You can add the same
number to both sides of an inequality and the statement
will still be true.
In numbers:
3 < 8
3 + 2 < 8 + 2
5 < 10
In Algebra:
𝑎 < 𝑏
𝑎 + 𝑐 < 𝑏 + 𝑐

12. Addition and Subtraction Properties of Inequality
Subtraction Property of Inequality: You can subtract
same number to both sides of an inequality and
statement will still be true.
In numbers:
3 < 8
3 − 2 < 8 − 2
1 < 6
In Algebra:
𝑎 < 𝑏
𝑎 − 𝑐 < 𝑏 – 𝑐

13. Solve the inequality 𝑚 + 12 < 20
𝒎 + 𝟏𝟐 < 𝟐𝟎
−𝟏𝟐 − 𝟏𝟐
Since 𝟏𝟐 is added to 𝒎,
subtract 12 both sides of the
inequality to undo the
𝒎 + 𝟎 < 𝟖 Simplify
𝒎 < 𝟖 Solution of the inequality
The solution set is { 𝒎: 𝒎 < 𝟖 }, read as, “𝒎 such that 𝒎 is less than 𝟖”.
𝒎 + 𝟏𝟐 < 𝟐𝟎 The given inequality

14. Solve the inequality 𝑏 – 5 > −7 and graph the solutions.
𝒃 – 𝟓 > −𝟕 The given inequality
𝒃 – 𝟓 > −𝟕
+𝟓 + 𝟓
Since 𝟓 is subtracted from 𝒃, add
𝟓 on both sides of the inequality
to undo the subtraction.
𝒃 + 𝟎 > −𝟐 Simplify
𝒃 > −𝟐 Solution of the inequality
𝒃 > −𝟐 is the solution of the inequality 𝒃 – 𝟓 > −𝟕

15. The solution set is {𝑏: 𝑏 > − 2}
◦ GRAPH

16. Solve the inequality 𝑡 + 1 ≤ 10
𝑡 + 1 ≤ 10 Write the inequality
𝑡 + 1 ≤ 10
−1 − 1
Since 1 is added to 𝑡, subtract 1
from both sides of the equation to
undo the addition.
𝑡 + 0 ≤ 9 Simplify
𝑡 ≤ 9 Solution of the inequality
𝑡 ≤ 9 is the solution of the inequality 𝑡 + 1 ≤ 10.

17. The solution set is {𝑡: 𝑡 ≤ 9}
◦ GRAPH

18. Multiplication and Division Property of Inequality
Multiplication Property of Inequality:
You can multiply both sides of an inequality by the same
number, and the statement will still be true.
In numbers:
7 < 12
7 3 < 12 3
21 < 36
In Algebra:
𝐼𝑓 𝑎 < 𝑏 𝑎𝑛𝑑 𝑐 > 0
𝑡ℎ𝑒𝑛 𝑎𝑐 < 𝑏𝑐

19. Multiplication and Division Property of Inequality
Division Property of Inequality:
You can multiply both sides of an inequality by the same
positive
number, and the statement will still be true.
In numbers:
15 < 35
15
5
<
35
5
3 < 7
In Algebra:
If 𝑎 < 𝑏 𝑎𝑛𝑑 𝑐 > 0
Then,
𝑎
𝑐
<
𝑏
𝑐

20. Solve the inequality 7𝑎 > −42
𝟕𝒂 > −𝟒𝟐 The given inequality
𝟕𝒂
𝟕
>
−𝟒𝟐
𝟕
Since 𝒂 is multiplied by 𝟕, divide
both sides by 𝟕 to undo the
multiplication operation.
𝟕𝒂
𝟕
>
−𝟒𝟐
𝟕
𝟏𝒂 > −𝟔
7 divided by 7 is 1; −𝟒𝟐 divided by
is −𝟔.
Note: The coefficient 1 does not necessarily be
written. Hence, the final solution shown below.
𝒂 > −𝟔 Solution of the inequality
𝒂 > −𝟔 is the solution of the inequality 𝟕𝒂 > −𝟒𝟐.

21. The solution set is {𝑎: 𝑎 > −6}
◦ GRAPH

22. Solve the inequality
3
4
𝑠 < 12
𝟑
𝟒
𝒔 < 𝟏𝟐
The given inequality
𝟒
𝟑
𝟑
𝟒
𝒔 < 𝟏𝟐
𝟒
𝟑
Since 𝒔 is multiplied by
𝟑
𝟒
, multiply
both sides by the reciprocal of
𝟑
𝟒
, which is
𝟒
𝟑
.
𝟏𝟐
𝟏𝟐
𝒔 <
𝟒𝟖
𝟑
𝟏𝒔 < 𝟏𝟔
Perform the operation on the left and the right of the
inequality symbol and simplify.
Note: The coefficient 1 does not necessarily be written. Hence, the final
shown below.
𝒔 < 𝟏𝟔 Solution of the inequality
𝒔 < 𝟏𝟔 is the solution of the inequality
𝟑
𝟒
𝒔 < 𝟏𝟐.

23. The solution set is {𝑠: 𝑠 < 16}
◦ GRAPH

24. Solve the inequality 4𝑐 > 24
4𝑐 > 24 The given inequality
4𝑐
4
>
24
4
Since 𝑐 is multiplied by 4, divide both sides
by 4 to undo multiplication.
4𝑐
4
>
24
4
1𝑐 > 6
4 divided by 4 is 1; 24 divided by 4 is 6.
Note: The coefficient 1 does not necessarily be written. Hence,
the final solution shown below.
𝑐 > 6 Solution of the inequality
𝑐 > 6 is the solution of the inequality 4𝑐 > 24.

25. The solution set is {c: c> 6}

26. Multiplication or Division of Negative Numbers on Inequalities
◦If you multiply or divide both sides of an
inequality by a negative number, flip or
reverse the direction of the inequality sign.

27. Solve the inequality −12𝑎 > 84
−12𝑎 > 84 The given Inequality
−12𝑎
−12
<
84
−12
Since 𝑎 is multiplied by −12, divide both sides by -
12 to undo multiplication. Then, change greater
than “>” to less than “<”.
−12𝑎
−12
<
84
−12
1𝑎 < −7
−12 divided by −12 is 1;
84 divided by −12 is −7.
Note: The coefficient 1 does not necessarily be written. Hence, the final
solution shown below.
𝑎 < −7 Solution of the inequality
𝑎 < −7 is the solution of the inequality −12𝑎 > 84.

28. The solution set is {𝑎: 𝑎 < −7}

29. Solve the inequality
𝑏
−3
≥ −8
𝑏
−3
≥ −8
The given inequality
−3
𝑏
−3
≤ −8 (−3)
Since 𝑏 is divided by −3, multiply both sides by −3
to undo division. Then, change greater than or equal
“≥” to less than or equal “≤”.
−3
𝑏
−3
≤ −8(−3)
1𝑏 ≤ 24
−3 divided by −3 is 1; −8 multiplied by −3 is 24.
𝑏 ≤ 24 Solution of the inequality
𝑏 ≤ 24 is the solution of the inequality
𝑏
−3
≥ −8.

30. The solution set is {𝑏: 𝑏 ≤ 24}

31. Solve the inequality − 𝑐 ≤ 10
− 𝑐 ≤ 10 The given inequality
(−1)(− 𝑐) ≥ 10(−1)
Multiply both sides by −1 to make 𝑐 positive.
Then, change less than or equal “≤” to greater
than or equal“≥”.
𝑐 ≥ −10 Solution of the inequality
𝑐 ≥ −10 is the solution of the inequality − 𝑐 ≤ 10

32. The solution set is {𝑐: 𝑐 ≥ −10}

33. ANSWER ACTIVITY
1. ANSWER ACTIVITY 3: EQUATION AND
INEQUALITY P. 96 (EDMODO)
2. ACTIVITY 5: FALL-ING FOR EQUALITIES
P.97(EDMODO)
3. OTHER ACTIVITY TO BE SENT AFTER THE
EDMODO ACTIVITY.(DROP IN THE DRIVE AND
ATTACH IN THE WEEKLY ACCOMPLISHMENT)
SEE NEXT SLIDES FOR ACTIVITY 3

34. ACTIVITY 3:
A. Solve the following Linear Inequalities. (show your complete steps)
B. Find the solution sets by set builder notation
C. Graph the solution set.
1.2(5x – 3) > 14
2.12x – 6 > 14x – 2
3.12 – ⅔ x > 6
4.3/5 x + 9 < 12
5.8(5x – 4) – 6(3x + 5) < -7

35. THANK YOU FOR
LISTENING!
SEE
YOU
AGAIN
NEXT
WEEK!