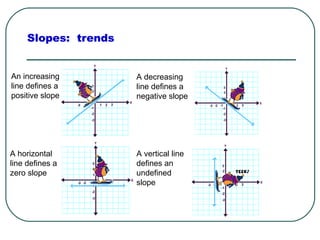
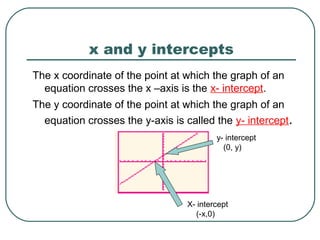
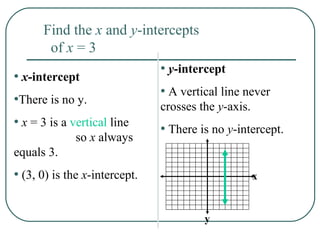
This document provides an overview of linear functions and equations. It defines linear equations as having the standard form Ax + By = C, with examples and how to identify linear vs. nonlinear equations. Linear functions are defined as having the form f(x) = mx + b. The document discusses slope, x-intercepts, y-intercepts, and how to graph linear equations from these components. It also covers representing linear functions in slope-intercept form as y = mx + b, and point-slope form as y - y1 = m(x - x1).

1. Linear Functions
linear equations, intercepts
and slopes

2. A linear equation is the equation
of a line.
The standard form of a linear equation is
Ax + By = C
* A has to be positive and cannot be a
fraction.

3. Examples of linear equations
2x + 4y =8
The equation is in the standard form
6y = 3 – x
x + 6y = 3
4x − y
= −7
3
4x - y = 21

4. Examples of Nonlinear Equations
The following equations are NOT in the
standard form of Ax + By =C:
4x2 + y = 5
x=4
xy + x = 5
s/r + r = 3
The exponent is 2
There is a radical in the equation
Variables are multiplied
Variables are divided

5. Determine whether the equation is a
linear equation, if so write it in
standard form.
y = 5 − 2x
2x + y = 5
y = x +3
This is not a linear equation since its in
the second degree
2
2 xy = −5 y + 6
1
x + 5y = 3
4
This is not a linear equation
since variables are multiplied
x + 20y = 12

6. DEFINITION OF A LINEAR
FUNCTION
A
linear function is a function of the form
f(x) = mx + b
where m and b are real numbers and m = 0

7. Transform the following into the form y = mx + b
x
+y=2
 2x
 8x
y = -x + 2
–y=5
y = 2x - 5
– 2y = 12
y = 4x - 6
 -3x
+ 2y = 6
y = 3x + 3
2

8. SLOPE OF A LINE
Slope refers to the steepness of a line.

9. Slopes: trends
An increasing
line defines a
positive slope
A decreasing
line defines a
negative slope
A horizontal
line defines a
zero slope
A vertical line
defines an
undefined
slope

10. Finding the slope of Linear
functions
What is the slope of a line passes through points (4,6) and (3,4)?
m=2

11. Determine the Slope of the following linear functions
that passes through the given pair of points
1. (3, 2), (6, 6)
2. (-9, 6), (-10, 3)
3. (-4, 2), (-5, 4)

12. x and y intercepts
The x coordinate of the point at which the graph of an
equation crosses the x –axis is the x- intercept.
The y coordinate of the point at which the graph of an
equation crosses the y-axis is called the y- intercept.
y- intercept
(0, y)
X- intercept
(-x,0)

13. Graph the linear equation using the
x- intercept and the y intercept
3x + 2y = 9
To find the x- intercept, let y = 0
3x + 2y = 9
3x + 2(0) = 9
3x = 9
x=3
Replace y with 0
Divide each side by 3
To find the y- intercept, let x = 0
3x + 2y = 9
3(0) + 2y = 9
2y = 9
y = 9/2
Replace x with 0
Divide each side by 2
Plot the two points and connect
them to draw the line.

14. 2x + y = 4
To find the x- intercept, let y = 0
2x + y = 4
Original Equation
2x + (0) = 4
2x =4
x=2
Replace y with 0
Divide each side by 3
To find the y- intercept, let x = 0
2x + y = 4
Original Equation
2(0) + y = 4
y=4
Replace x with 0
Simplify
Plot the two points and connect them to draw the line.

15. Find the x and y- intercepts
of x = 4y – 5
●
●
●
x-intercept:
Plug in y = 0
x = 4y - 5
x = 4(0) - 5
x=0-5
x = -5
(-5, 0) is the
x-intercept
●
●
y-intercept:
Plug in x = 0
x = 4y - 5
0 = 4y - 5
5 = 4y
5
=y
4
5
● (0, )
4
is the
y-intercept

16. Find the x and y-intercepts
of g(x) = -3x – 1*
●
●
x-intercept
1
( − , 0) is the
3
x-intercept
*g(x) is the same as y
●
●
y-intercept
(0, -1) is the
y-intercept

17. Find the x and y-intercepts
of x = 3
●
x-intercept
●There
is no y.
x = 3 is a vertical line
so x always
equals 3.
●
●
●
y-intercept
A vertical line never
crosses the y-axis.
●
●
There is no y-intercept.
(3, 0) is the x-intercept.
x
y

18. Find the x and y-intercepts
of y = -2
●
x-intercept
Plug in y = 0.
y cannot = 0 because
y = -2.
● y = -2 is a horizontal
line so it never crosses
the x-axis.
●
●There
●
y-intercept
●
y = -2 is a horizontal line
so y always equals -2.
●
(0,-2) is the y-intercept.
x
is no x-intercept.
y

19. EQUATION OF A LINEAR
FUNCTION
 Slope-
Intercept form
y = mx + b

20. y = mx + b

Give the equation of the linear function y in slope
intercept form given its slope and y-intercept
1. m = -3, b = 2
2. m= 2, b = - 4
3. M = 1/3, b = 3

21. EQUATION OF A LINEAR
FUNCTION
 Point-Slope
form
y –y1= m(x – x1)

22. y –y1= m(x – x1)

Give the equation of the linear function y with the
given slope and passing through given points.
1. m = 2, through (1, 2)
2. m= -3, through (5, 0)
3. m = -1/3, through (-1, 3)

23. EQUATION OF A LINEAR
FUNCTION

24. 
Give the equation of the linear function y with the
given slope and passing through given points.
1. through (1, 2) and (3, -2)
2. through (5, 0) and (-1, 3)

25. EQUATION OF A LINEAR
FUNCTION
 Intercept
Form
_x_ + _y_
a
b
= 1

26. Questions??