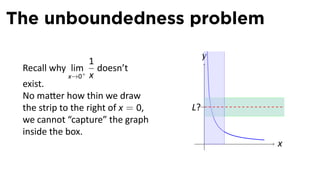
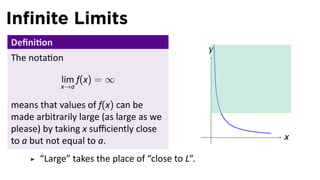
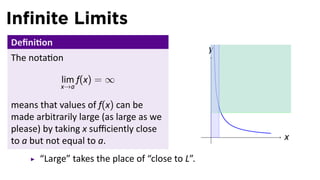
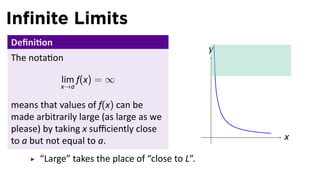
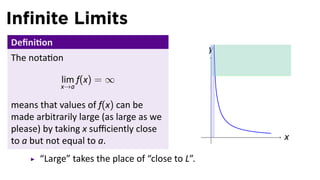
The document focuses on understanding limits involving infinity in calculus, specifically how to intuit and algebraically determine these limits. It covers definitions of limits, vertical asymptotes, and the behavior of functions approaching infinite limits or discontinuities. Additionally, the document outlines limit laws and essential rules regarding operations involving finite and infinite limits.