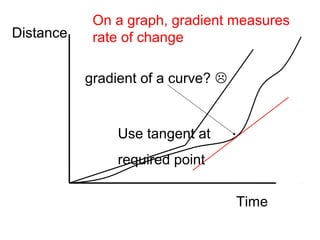
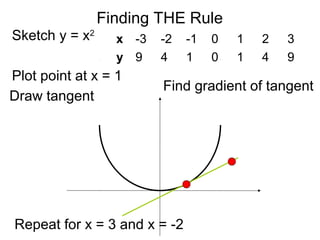
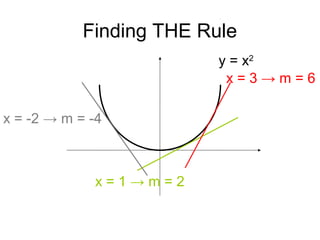
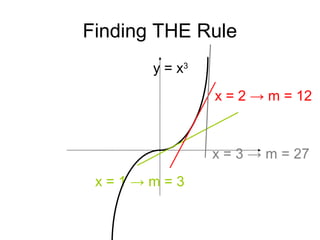
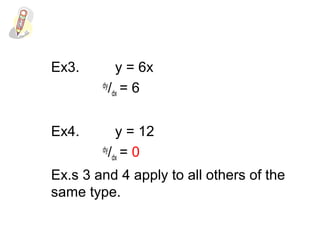The document introduces differentiation and the concept of the derivative. It discusses how the derivative can be used to find the rate of change of a function and the slope of its tangent line. The main rules covered are: 1) If f(x) = x^n, then the derivative is f'(x) = nx^(n-1). 2) Examples are provided of finding the derivative of functions like f(x) = 6x^3, which is f'(x) = 18x^2. 3) The derivative can be used to find the slope of a tangent line at specific points, like finding the derivative of f(x) = (x + 5)^2 at x

1. Block 1
Introduction to Differentiation

2. What is Being Learned?
• What differentiation is
• Rule to differentiate
• Know what the derivative is.

3. Consider
how quickly a flower grows
the water level in a barrel
decreasing due to a leak
how fast a rocket goes
All to do with
rates of change

4. Distance
Time
On a graph, gradient measures
rate of change
gradient of a curve? 
Use tangent at
required point

5. Finding THE Rule
Sketch y = x2
x -3 -2 -1 0 1 2 3
y 9 4 1 0 1 4 9
Plot point at x = 1
Draw tangent
Find gradient of tangent
Repeat for x = 3 and x = -2

6. Finding THE Rule
y = x2
x = 1 → m = 2
x = 3 → m = 6
x = -2 → m = -4

7. Finding THE Rule
x m
1 2
3 6
-2 -4
Rule for y = x2
m = 2x

8. Finding THE Rule
y = x3
x = 1 → m = 3
x = 2 → m = 12
x = 3 → m = 27

9. Finding THE Rule
x m
1 3
2 12
3 27
Rule for y = x3
m = x2
X 3
= 3x2
X 3
X 3X 2
X 3X 3
X 1

10. Summarising
y = x2
m = 2x
y = x3
m = 3x2
y = x4
m = x
43
The gradient to the
curve rule is known as
The Derivative

11. Applying the Rule
y = x8
derivative = 8x7
y = x11
derivative = 11x10
y = 5x3
derivative = 3 X 5x2
= 15x2

12. Applying the Rule
y = 4x2
derivative = 8x1
(usually written 8x)
y = 6x3
derivative = 18x2
Nasty y = 5x
derivative = 5x0
= 5
same as 5x1

13. Even Nastier?
y = 10
Derivative = 0
Easiest just to remember these last two
as separate rules
same as 10x0

14. About the Derivative
• Has its own rule
Gives you
• Gradient of a curve (and the tangent to
curve)
• Rates of change
More to come!

15. Derivative Symbols
Depend on way equation is given
Ex f(x) = 2x5
f/
(x) = 10x4

16. Derivative Symbols
Depend on way equation is given
Ex y = 5x3
dy
/dx = 15x2

17. Differentiation
THE rule
if y = axn
then dy
/dx= nax n-1
Known as the derivative

18. Ex1. y = 6x3
dy
/dx = 18x2
Ex2. f(x) = 8x4
f/
(x)= 32x3
Another way to write
the derivative

19. Ex3. y = 6x
dy
/dx = 6
Ex4. y = 12
dy
/dx = 0
Ex.s 3 and 4 apply to all others of the
same type.

20. Derivative Calculations
If f(x) = 3x2
– 8x + 12 , calculate f/
(3)
f/
(x) = 6x – 8
f/
(3) = 6(3) – 8
= 10

21. Uses of the Derivative (so far)
• Gives gradient of tangent to any curve
• Gives rates of change

22. Derivative Calculations
If f(x) = 2x3
+ 7x – 4, calculate f/
(4)
f/
(x) = 6x2
+ 7
f/
(4) = 6(42
) + 7
= 103
(very steep!!!!!!!!!!!!)

23. Key Question
If f(x) = (x + 5)2
, calculate f/
(4)
f(x) = (x + 5)(x + 5)
= x2
+ 10x + 25
f/
(x) = 2x + 10
f/
(4) = 2(4) + 10
= 18