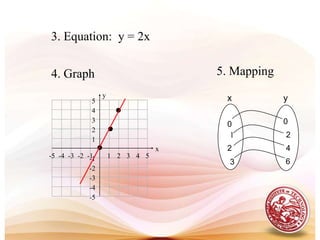
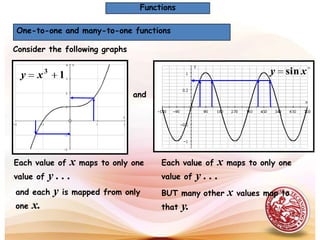
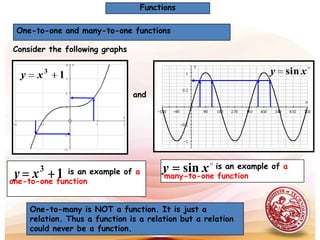
This document defines functions and relations. It discusses identifying the domain and range of functions and relations, evaluating functions, and performing operations on functions such as addition, subtraction, multiplication, division, and composition. It also covers graphing functions, including piecewise functions, absolute value functions, greatest and least integer functions. Key examples are provided to illustrate how to identify domains and ranges, evaluate functions, perform operations on functions, and graph different types of functions.

1. FunctionsPrepared by:Teresita P. Liwanag - Zapanta

2. OBJECTIVESdistinguish functions and relations

3. identify domain and range of a function/relationevaluate functions/relations.perform operation on functions/relations

4. graph functions/relationsDEFINITIONRelation is referred to as any set of ordered pair.Conventionally, It is represented by the ordered pair ( x , y ). x is called the first element or x-coordinate while y is the second element or y-coordinate of the ordered pair.

5. Ways of Expressing a Relation4. Graph1. Set notation5. Mapping2. Tabular form3. Equation

6. Example: Express the relation y = 2x;x= 0,1,2,3 in 5 ways..1. Set notation (a) S = { ( 0, 0) , ( 1, 2 ) , ( 2, 4 ), ( 3, 6) } or (b) S = { (x , y) such that y = 2x, x = 0, 1, 2, 3 }2. Tabular form

7. y554321x5-4-2135-5-14-32-5-1-2-3-4-5-53. Equation: y = 2x5. Mapping4. Graphxy●00●12●2463

8. DEFINITION: Domain and RangeAll the possible values of x is called the domain and all the possible values of y is called the range. In a set of ordered pairs, the set of first elements and second elements of ordered pairs is the domain and range, respectively.Example: Identify the domain and range of the following relations. 1.) S = { ( 4, 7 ),( 5, 8 ),( 6, 9 ),( 7, 10 ),( 8, 11 ) } Answer : D: { 4,5,6,7,8} R:{7,8,9,10,11}

9. 2.) S = { ( x , y ) s. t. y = | x | ; x  R } Answer: D: all real nos.R: all real nos. > 03) y = x 2 – 5 Answer. D: all real nos. R: all real nos. > -5 4) | y | = x Answer: D: all real nos. > 0 R: all real nos.

10. g) Answer: D: all real nos. except -2 R: all real nos. except 2 5. Answer : D: all real nos. > –1 R: all real nos. > 06.Answer:D: all real nos. < 3 R: all real nos. except 07.

11. Exercises: Identify the domain and range of the following relations. 1. {(x,y) | y = x 2 – 4 }2. 5. 7. y = 25 – x 2y = | x – 7 |6. 4. 3. 8. y = (x 2 – 3) 29. 10.

12. PROBLEM SET #5-1FUNCTIONSIdentify the domain and range of the following relations.

13. Definition: FunctionA function is a special relation such that every first element is paired to a unique second element.

14. It is a set of ordered pairs with no two pairs having the same first element.FunctionsOne-to-one and many-to-one functions Consider the following graphsandEach value of x maps to only one value of y . . .Each value of x maps to only one value of y . . .and each y is mapped from only one x.BUT manyother x values map to that y.

15. is an example of a many-to-one functionis an example of a one-to-one function FunctionsOne-to-one and many-to-one functions Consider the following graphsandOne-to-many is NOT a function. It is just a relation. Thus a function is a relation but a relation could never be a function.

16. Example: Identify which of the following relations are functions.a) S = { ( 4, 7 ), ( 5, 8 ), ( 6, 9 ), ( 7, 10 ), ( 8, 11 ) } b) S = { ( x , y ) s. t. y = | x | ; x  R }c) y = x 2 – 5 d) | y | = x e)f)

17. DEFINITION: Function NotationLetters like f , g , h and the likes are used to designate functions.

18. When we use f as a function, then for each x in the domain of f , f ( x ) denotes the image of x under f .

19. The notation f ( x ) is read as “ f of x”.EXAMPLE: Evaluate each function value1. If f ( x ) = x + 9 , what is the value of f ( x 2 ) ?2. If g ( x ) = 2x – 12 , what is the value of g (– 2 )?3. If h ( x ) = x 2 + 5 , find h ( x + 1 ).If f(x) = x – 2 and g(x) = 2x2 – 3 x – 5 , Find: a) f(g(x)) b) g(f(x))

20. Piecewise Defined FunctionA piecewise defined function is defined by different formulas on different parts of its domain. Example:if x<0 if

21. Piecewise Defined FunctionEXAMPLE: Evaluate the piecewise function at the indicated values.if x<0 f(-2), f(-1), f(0), f(1), f(2)ifififif f(-5), f(0), f(1), f(5)

22. DEFINITION: Operations on FunctionsIf f (x) and g (x) are two functions, thenSum and Difference ( f + g ) ( x ) = f(x) + g(x) Product( f g ) ( x ) = [ f(x) ] [ g(x) ] Quotient( f / g ) ( x ) = f(x) / g(x) d) Composite ( f ◦ g ) ( x ) = f (g(x))

23. Example :1. Given f(x) = 11– x and g(x) = x 2 +2x –10 evaluate each ofthe following functionsf(-5) g(2)(f g)(5)(f - g)(4)f(7)+g(x)g(-1) – f(-4)(f ○ g)(x)(g ○ f)(x)(g ○ f)(2)(f○ g)

26. DEFINITION: Graph of a Function If f(x) is a function, then its graph is the set of all points (x,y) in the two-dimensional plane for which (x,y) is an ordered pair in f(x)One way to graph a function is by point plotting.

27. We can also find the domain and range from the graph of a function.

28. Example: Graph each of the following functions.6.

29. Graph of piecewise defined functionThe graph of a piecewise function consists of separate functions.Example: Graph each piecewise function.ififififif

30. Plot the points in the coordinate planeyx-21

31. Plot the points in the coordinate planeyx-21

32. Graph of absolute value function.Recall thatififUsing the same method that we used in graphingpiecewise function, we note that the graph of f coincides with the line y=x to the right of the y axisand coincides with the line y= -x the left of the y-axis.

33. Example: Graph each of the follow functions.y = | x – 7 |y = x-| x - 2 |1. 4.

34. Plot the points in the coordinate planeyx-21

36. Definition: Greatest integer function.The greatest integer function is defined by greatest integer less than or equal to xExample: 130-410-1102021

37. Definition: Least integer function.The least integer function is defined byleast integer greater than or equal to xExample: 240-3210212131

38. Graph of greatest integer function.Sketch the graph of