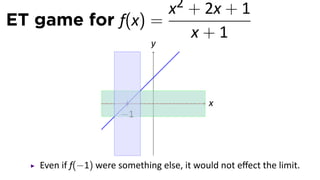
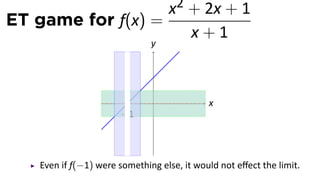
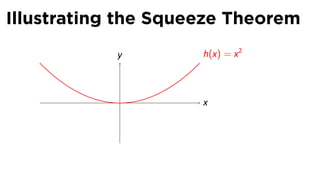
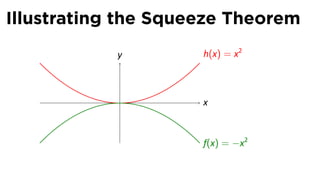
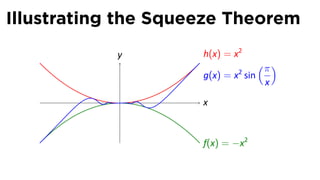
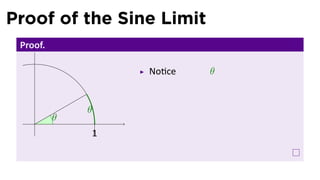
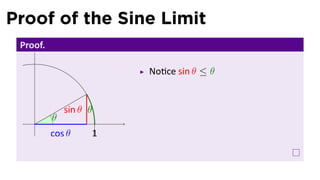
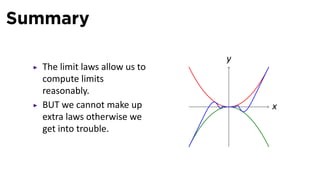
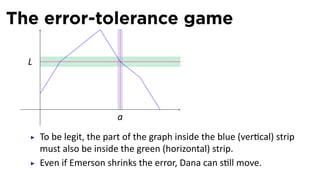
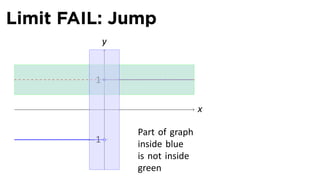
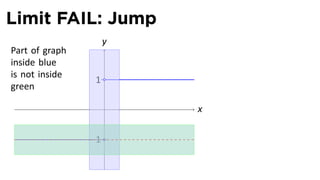
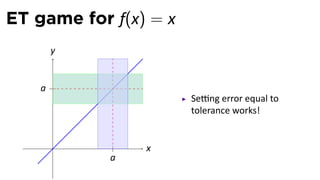
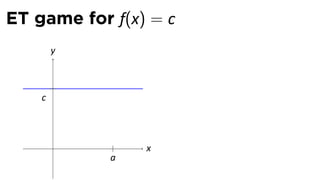
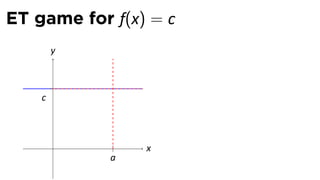
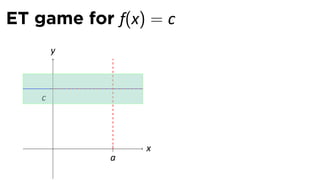
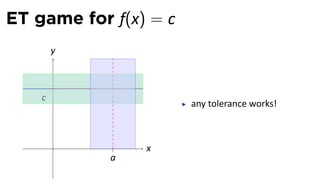
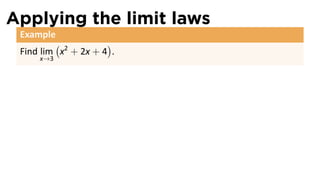The document discusses limits and the limit laws. It introduces the concept of a limit using an "error-tolerance" game. It then proves some basic limits, such as the limit of x as x approaches a equals a, and the limit of a constant c equals c. It explains the limit laws for addition, subtraction, multiplication, division and nth roots of functions. It uses the error-tolerance game framework to justify the limit laws.








![Limit EPIC FAIL (π )
Here is a graph of the func on f(x) = sin :
x
y
1
. x
−1
For every y in [−1, 1], there are infinitely many points x arbitrarily
close to zero where f(x) = y. So lim f(x) cannot exist.
x→0](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-14-320.jpg)



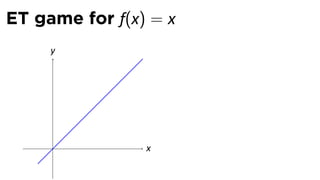
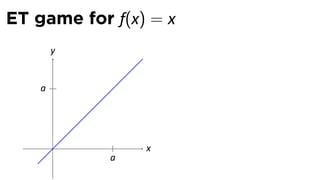
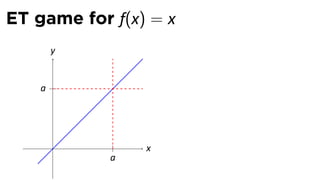
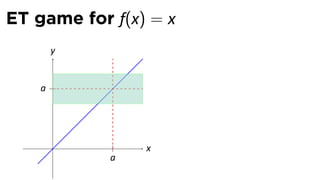
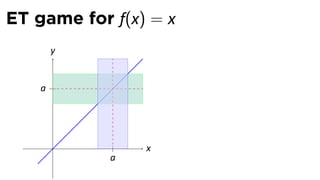



![Limits and arithmetic
Fact
Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = L + M
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-34-320.jpg)
![Limits and arithmetic
Fact
Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = L + M (errors add)
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-35-320.jpg)
![Limits and arithmetic
Fact
Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = L + M (errors add)
x→a
2. lim [f(x) − g(x)] = L − M
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-36-320.jpg)
![Limits and arithmetic
Fact
Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = L + M (errors add)
x→a
2. lim [f(x) − g(x)] = L − M
x→a
3. lim [cf(x)] = cL
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-37-320.jpg)
![Limits and arithmetic
Fact
Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = L + M (errors add)
x→a
2. lim [f(x) − g(x)] = L − M
x→a
3. lim [cf(x)] = cL (error scales)
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-38-320.jpg)

![Limits and arithmetic
Fact
Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = L + M (errors add)
x→a
2. lim [f(x) − g(x)] = L − M (combina on of adding and scaling)
x→a
3. lim [cf(x)] = cL (error scales)
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-40-320.jpg)
![Limits and arithmetic
Fact
Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = L + M (errors add)
x→a
2. lim [f(x) − g(x)] = L − M (combina on of adding and scaling)
x→a
3. lim [cf(x)] = cL (error scales)
x→a
4. lim [f(x)g(x)] = L · M
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-41-320.jpg)
![Limits and arithmetic
Fact
Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = L + M (errors add)
x→a
2. lim [f(x) − g(x)] = L − M (combina on of adding and scaling)
x→a
3. lim [cf(x)] = cL (error scales)
x→a
4. lim [f(x)g(x)] = L · M (more complicated, but doable)
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-42-320.jpg)


![Limits and arithmetic II
Fact (Con nued)
f(x) L
5. lim = , if M ̸= 0.
x→a g(x) M
[ ]n
n
6. lim [f(x)] = lim f(x)
x→a x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-45-320.jpg)
![Limits and arithmetic II
Fact (Con nued)
f(x) L
5. lim = , if M ̸= 0.
x→a g(x) M
[ ]n
n
6. lim [f(x)] = lim f(x) (follows from 4 repeatedly)
x→a x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-46-320.jpg)
![Limits and arithmetic II
Fact (Con nued)
f(x) L
5. lim = , if M ̸= 0.
x→a g(x) M
[ ]n
n
6. lim [f(x)] = lim f(x) (follows from 4 repeatedly)
x→a x→a
n n
7. lim x = a
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-47-320.jpg)
![Limits and arithmetic II
Fact (Con nued)
f(x) L
5. lim = , if M ̸= 0.
x→a g(x) M
[ ]n
n
6. lim [f(x)] = lim f(x) (follows from 4 repeatedly)
x→a x→a
n n
7. lim x = a
x→a
√ √
8. lim n x = n a
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-48-320.jpg)
![Limits and arithmetic II
Fact (Con nued)
f(x) L
5. lim = , if M ̸= 0.
x→a g(x) M
[ ]n
n
6. lim [f(x)] = lim f(x) (follows from 4 repeatedly)
x→a x→a
n n
7. lim x = a (follows from 6)
x→a
√ √
8. lim n x = n a
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-49-320.jpg)
![Limits and arithmetic II
Fact (Con nued)
f(x) L
5. lim = , if M ̸= 0.
x→a g(x) M
[ ]n
n
6. lim [f(x)] = lim f(x) (follows from 4 repeatedly)
x→a x→a
n n
7. lim x = a (follows from 6)
x→a
√ √
8. lim n x = n a
x→a
√ √
n
9. lim f(x) = n lim f(x) (If n is even, we must addi onally
x→a x→a
assume that lim f(x) > 0)
x→a](https://image.slidesharecdn.com/lesson04-calculatinglimits001slides-110203072109-phpapp01-121002033911-phpapp01/85/Lesson-4-Calculating-Limits-slides-50-320.jpg)