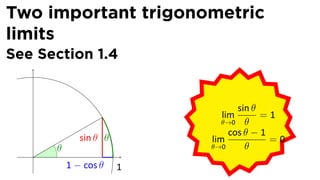
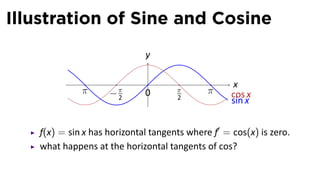
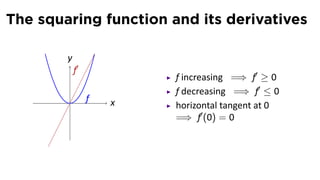
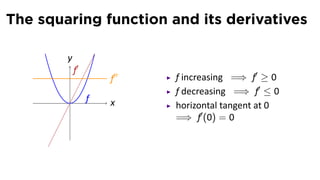
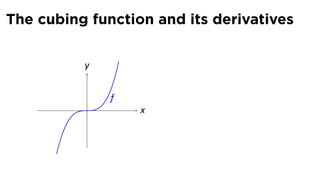
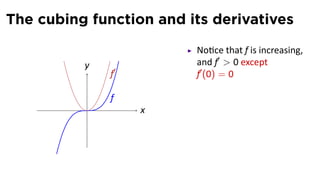
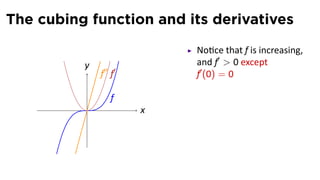
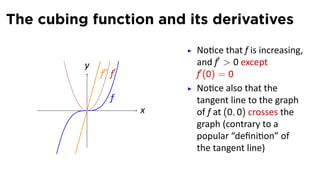
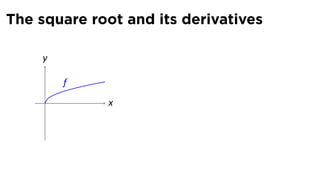
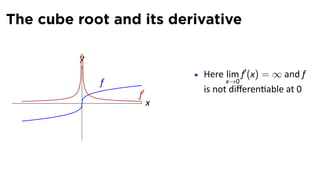
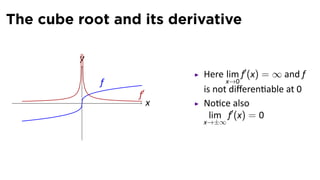
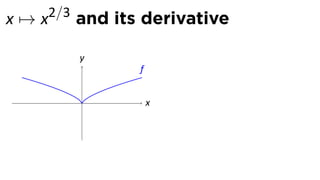
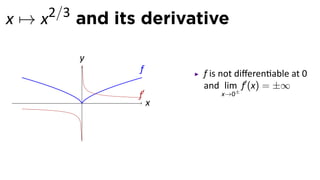
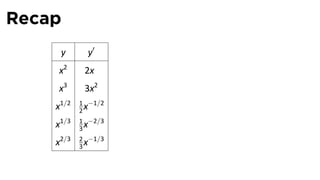
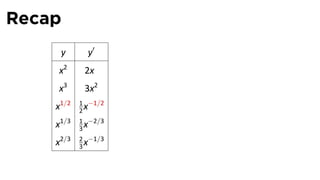
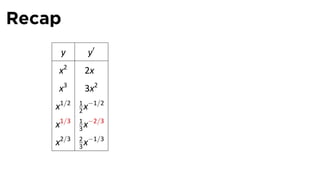
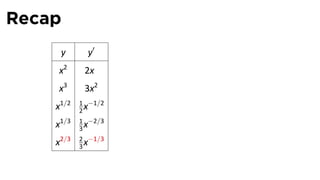
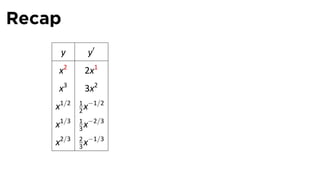
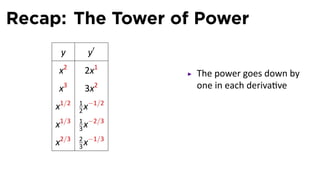
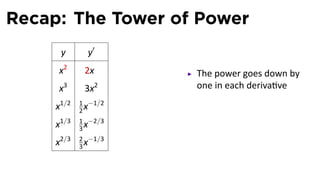
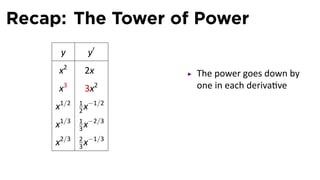
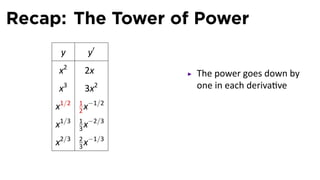
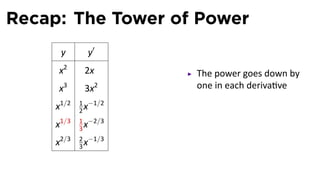
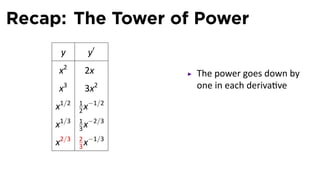
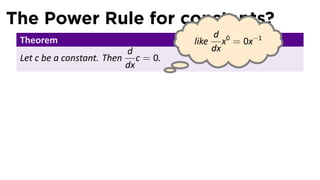
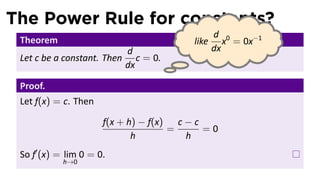
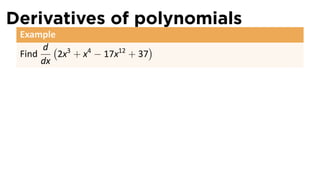This document provides an outline for a calculus lecture on basic differentiation rules. It includes objectives to understand key rules like the constant multiple rule, sum rule, and derivatives of sine and cosine. Examples are worked through to find the derivatives of functions like squaring, cubing, square root, and cube root using the definition of the derivative. Graphs and properties of derived functions are also discussed.

1. Sec on 2.3
Basic Differenta on Rules
V63.0121.011: Calculus I
Professor Ma hew Leingang
New York University
. NYUMathematics

2. Announcements
Quiz 1 this week on
1.1–1.4
Quiz 2 March 3/4 on 1.5,
1.6, 2.1, 2.2, 2.3
Midterm Monday March
7 in class

3. Objectives
Understand and use
these differen a on
rules:
the deriva ve of a
constant func on (zero);
the Constant Mul ple
Rule;
the Sum Rule;
the Difference Rule;
the deriva ves of sine
and cosine.

4. Recall: the derivative
Defini on
Let f be a func on and a a point in the domain of f. If the limit
f(a + h) − f(a) f(x) − f(a)
f′ (a) = lim = lim
h→0 h x→a x−a
exists, the func on is said to be differen able at a and f′ (a) is the
deriva ve of f at a.

5. The deriva ve …
…measures the slope of the line through (a, f(a)) tangent to
the curve y = f(x);
…represents the instantaneous rate of change of f at a
…produces the best possible linear approxima on to f near a.

6. Notation
Newtonian nota on Leibnizian nota on
dy d df
f′ (x) y′ (x) y′ f(x)
dx dx dx

7. Link between the notations
f(x + ∆x) − f(x) ∆y dy
f′ (x) = lim = lim =
∆x→0 ∆x ∆x→0 ∆x dx
dy
Leibniz thought of as a quo ent of “infinitesimals”
dx
dy
We think of as represen ng a limit of (finite) difference
dx
quo ents, not as an actual frac on itself.
The nota on suggests things which are true even though they
don’t follow from the nota on per se

8. Outline
Deriva ves so far
Deriva ves of power func ons by hand
The Power Rule
Deriva ves of polynomials
The Power Rule for whole number powers
The Power Rule for constants
The Sum Rule
The Constant Mul ple Rule
Deriva ves of sine and cosine

9. Derivative of the squaring function
Example
Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x).

10. Derivative of the squaring function
Example
Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x).
Solu on
f(x + h) − f(x)
f′ (x) = lim
h→0 h

11. Derivative of the squaring function
Example
Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x).
Solu on
′ f(x + h) − f(x) (x + h)2 − x2
f (x) = lim = lim
h→0 h h→0 h

12. Derivative of the squaring function
Example
Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x).
Solu on
′ f(x + h) − f(x) (x + h)2 − x2
f (x) = lim = lim
h→0 h h→0 h
+ 2xh + h −
2
x2
x2
= lim
h→0 h

13. Derivative of the squaring function
Example
Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x).
Solu on
′ f(x + h) − f(x) (x + h)2 − x2
f (x) = lim = lim
h→0 h h→0 h
+ 2xh + h −
x2
2
x2
2x + h2
h
¡
= lim = lim
h→0 h h→0 h

14. Derivative of the squaring function
Example
Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x).
Solu on
′ f(x + h) − f(x) (x + h)2 − x2
f (x) = lim = lim
h→0 h h→0 h
+ 2xh + h −
x2
2
x2
2x + h2
h
¡
= lim = lim
h→0 h h→0 h
= lim (2x + h) = 2x.
h→0

15. The second derivative
If f is a func on, so is f′ , and we can seek its deriva ve.
f′′ = (f′ )′
It measures the rate of change of the rate of change!

16. The second derivative
If f is a func on, so is f′ , and we can seek its deriva ve.
f′′ = (f′ )′
It measures the rate of change of the rate of change! Leibnizian
nota on:
d2 y d2 d2 f
f(x)
dx2 dx2 dx2

17. The squaring function and its derivatives
y
. x

18. The squaring function and its derivatives
y
. f x

19. The squaring function and its derivatives
y
f′
f increasing =⇒ f′ ≥ 0
f decreasing =⇒ f′ ≤ 0
. f x horizontal tangent at 0
=⇒ f′ (0) = 0

20. The squaring function and its derivatives
y
f′
f′′ f increasing =⇒ f′ ≥ 0
f decreasing =⇒ f′ ≤ 0
. f x horizontal tangent at 0
=⇒ f′ (0) = 0

21. Derivative of the cubing function
Example
Suppose f(x) = x3 . Use the defini on of deriva ve to find f′ (x).

22. Derivative of the cubing function
Example
Suppose f(x) = x3 . Use the defini on of deriva ve to find f′ (x).
Solu on
′ f(x + h) − f(x) (x + h)3 − x3
f (x) = lim = lim
h→0 h h→0 h

23. Derivative of the cubing function
Example
Suppose f(x) = x3 . Use the defini on of deriva ve to find f′ (x).
Solu on
′ f(x + h) − f(x) (x + h)3 − x3
f (x) = lim = lim
h→0 h h→0 h
x3
+ 3x2 h + 3xh2 + h3 − 3
x
= lim
h→0 h

24. Derivative of the cubing function
Example
Suppose f(x) = x3 . Use the defini on of deriva ve to find f′ (x).
Solu on
′ f(x + h) − f(x) (x + h)3 − x3
f (x) = lim = lim
h→0 h h→0 h
1 2
!
¡ !
¡
x3
+
2 2
3x h + 3xh + h 3
− 3
x 3x2 +
h
¡
3xh2 + ¡
h3
= lim = lim
h→0 h h→0 h

25. Derivative of the cubing function
Example
Suppose f(x) = x3 . Use the defini on of deriva ve to find f′ (x).
Solu on
′ f(x + h) − f(x) (x + h)3 − x3
f (x) = lim = lim
h→0 h h→0 h
1 2
!
¡ !
¡
x3
2 2
3x h + 3xh + h
+
3
− 3
x 3x2 +
h
¡
3xh2 + ¡
h3
= lim = lim
h→0
( 2 h ) h→0 h
= lim 3x + 3xh + h2 = 3x2 .
h→0

26. The cubing function and its derivatives
y
. x

27. The cubing function and its derivatives
y
f
. x

28. The cubing function and its derivatives
No ce that f is increasing,
y and f′ 0 except
f′ f′ (0) = 0
f
. x

29. The cubing function and its derivatives
No ce that f is increasing,
y and f′ 0 except
f′′ f′ f′ (0) = 0
f
. x

30. The cubing function and its derivatives
No ce that f is increasing,
y and f′ 0 except
f′′ f′ f′ (0) = 0
No ce also that the
f tangent line to the graph
. x of f at (0, 0) crosses the
graph (contrary to a
popular “defini on” of
the tangent line)

31. Derivative of the square root
Example
√
Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on.

32. Derivative of the square root
Example
√
Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on.
Solu on
√ √
′ f(x + h) − f(x) x+h− x
f (x) = lim = lim
h→0 h h→0 h

33. Derivative of the square root
Example
√
Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on.
Solu on
√ √
′ f(x + h) − f(x) x+h− x
f (x) = lim = lim
h→0
√ h h→0 h
√ √ √
x+h− x x+h+ x
= lim ·√ √
h→0 h x+h+ x

34. Derivative of the square root
Example
√
Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on.
Solu on
√ √
′ f(x + h) − f(x) x+h− x
f (x) = lim = lim
h→0
√ h h→0 h
√ √ √
x+h− x x+h+ x
= lim ·√ √
h→0 h x+h+ x
(x + h) − x
¡ ¡
= lim (√ √ )
h→0 h x+h+ x

35. Derivative of the square root
Example
√
Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on.
Solu on
√ √
′ f(x + h) − f(x) x+h− x
f (x) = lim = lim
h→0
√ h h→0 h
√ √ √
x+h− x x+h+ x
= lim ·√ √
h→0 h x+h+ x
(x + h) − x
¡ ¡ h
= lim (√ √ ) = lim (√ √ )
h→0 h x+h+ x h x+h+ x
h→0

36. Derivative of the square root
Example
√
Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on.
Solu on
√ √
′ f(x + h) − f(x) x+h− x
f (x) = lim = lim
h→0
√ h h→0 h
√ √ √
x+h− x x+h+ x
= lim ·√ √
h→0 h x+h+ x
(x + h) − x
¡ ¡ h
1
= lim (√ √ ) = lim (√ √ )= √
h→0 h x+h+ x h x+h+ x
h→0 2 x

37. The square root and its derivatives
y
. x

38. The square root and its derivatives
y
f
. x

39. The square root and its derivatives
y
f Here lim+ f′ (x) = ∞ and f
x→0
f′ is not differen able at 0
. x

40. The square root and its derivatives
y
f Here lim+ f′ (x) = ∞ and f
x→0
f′ is not differen able at 0
. x
No ce also lim f′ (x) = 0
x→∞

41. Derivative of the cube root
Example
√
Suppose f(x) = 3
x = x1/3 . Find f′ (x).

42. Derivative of the cube root
Example
√
Suppose f(x) = 3
x = x1/3 . Find f′ (x).
Solu on
f(x + h) − f(x) (x + h)1/3 − x1/3
f′ (x) = lim = lim
h→0 h h→0 h

43. Derivative of the cube root
Example
√
Suppose f(x) = 3
x = x1/3 . Find f′ (x).
Solu on
f(x + h) − f(x) (x + h)1/3 − x1/3
f′ (x) = lim = lim
h→0 h h→0 h
(x + h) − x
1/3 1/3
(x + h) + (x + h)1/3 x1/3 + x2/3
2/3
= lim ·
h→0 h (x + h)2/3 + (x + h)1/3 x1/3 + x2/3

44. Derivative of the cube root
Example
√
Suppose f(x) = 3
x = x1/3 . Find f′ (x).
Solu on
f(x + h) − f(x) (x + h)1/3 − x1/3
f′ (x) = lim = lim
h→0 h h→0 h
(x + h) − x
1/3 1/3
(x + h) + (x + h)1/3 x1/3 + x2/3
2/3
= lim ·
h→0 h (x + h)2/3 + (x + h)1/3 x1/3 + x2/3
(x + h) − x
¡ ¡
= lim 2/3 + (x + h)1/3 x1/3 + x2/3 )
h→0 h ((x + h)

45. Derivative of the cube root
Example
√
Suppose f(x) = 3
x = x1/3 . Find f′ (x).
Solu on
f(x + h) − f(x) (x + h)1/3 − x1/3
f′ (x) = lim = lim
h→0 h h→0 h
(x + h) − x
1/3 1/3
(x + h) + (x + h)1/3 x1/3 + x2/3
2/3
= lim ·
h→0 h (x + h)2/3 + (x + h)1/3 x1/3 + x2/3
(x + h) − x
¡ ¡
= lim 2/3 + (x + h)1/3 x1/3 + x2/3 )
h→0 h ((x + h)
h
= lim 2/3 + (x + h)1/3 x1/3 + x2/3 )
h→0 ((x + h)
h

46. Derivative of the cube root
Example
√
Suppose f(x) = 3
x = x1/3 . Find f′ (x).
Solu on
f(x + h) − f(x) (x + h)1/3 − x1/3
f′ (x) = lim = lim
h→0 h h→0 h
(x + h) − x
1/3 1/3
(x + h) + (x + h)1/3 x1/3 + x2/3
2/3
= lim ·
h→0 h (x + h)2/3 + (x + h)1/3 x1/3 + x2/3
(x + h) − x
¡ ¡
= lim 2/3 + (x + h)1/3 x1/3 + x2/3 )
h→0 h ((x + h)
h
1
= lim 2/3 + (x + h)1/3 x1/3 + x2/3 )
= 2/3
h→0 ((x + h)
h 3x

47. The cube root and its derivative
y
. x

48. The cube root and its derivative
y
f
. x

49. The cube root and its derivative
y
Here lim f′ (x) = ∞ and f
f x→0
is not differen able at 0
f′
. x

50. The cube root and its derivative
y
Here lim f′ (x) = ∞ and f
f x→0
is not differen able at 0
f′
. x No ce also
lim f′ (x) = 0
x→±∞

51. One more
Example
Suppose f(x) = x2/3 . Use the defini on of deriva ve to find f′ (x).

52. One more
Example
Suppose f(x) = x2/3 . Use the defini on of deriva ve to find f′ (x).
Solu on
f(x + h) − f(x) (x + h)2/3 − x2/3
f′ (x) = lim = lim
h→0 h h→0 h

53. One more
Example
Suppose f(x) = x2/3 . Use the defini on of deriva ve to find f′ (x).
Solu on
f(x + h) − f(x) (x + h)2/3 − x2/3
f′ (x) = lim = lim
h→0 h h→0 h
1/3 ( )
(x + h) − x
1/3
= lim · (x + h) + x
1/3 1/3
h→0 h

54. One more
Example
Suppose f(x) = x2/3 . Use the defini on of deriva ve to find f′ (x).
Solu on
f(x + h) − f(x) (x + h)2/3 − x2/3
f′ (x) = lim = lim
h→0 h h→0 h
1/3 ( )
(x + h) − x
1/3
= lim · (x + h) + x
1/3 1/3
h→0
( h)
1 −2/3
= 3x 2x1/3

55. One more
Example
Suppose f(x) = x2/3 . Use the defini on of deriva ve to find f′ (x).
Solu on
f(x + h) − f(x) (x + h)2/3 − x2/3
f′ (x) = lim = lim
h→0 h h→0 h
1/3 ( )
(x + h) − x
1/3
= lim · (x + h) + x
1/3 1/3
h→0
( h)
1 −2/3
= 3x 2x1/3 = 2 x−1/3
3

56. x → x2/3 and its derivative
y
. x

57. x → x2/3 and its derivative
y
f
. x

58. x → x2/3 and its derivative
y
f f is not differen able at 0
and lim± f′ (x) = ±∞
f′ x→0
. x

59. x → x2/3 and its derivative
y
f f is not differen able at 0
and lim± f′ (x) = ±∞
f′ x→0
. x No ce also
lim f′ (x) = 0
x→±∞

60. Recap
y y′
x2 2x
x3 3x2
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

61. Recap
y y′
x2 2x
x3 3x2
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

62. Recap
y y′
x2 2x
x3 3x2
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

63. Recap
y y′
x2 2x
x3 3x2
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

64. Recap
y y′
x2 2x
x3 3x2
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

65. Recap
y y′
x2 2x1
x3 3x2
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

66. Recap: The Tower of Power
y y′
x2 2x1 The power goes down by
x 3
3x2 one in each deriva ve
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

67. Recap: The Tower of Power
y y′
x2 2x The power goes down by
x 3
3x2 one in each deriva ve
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

68. Recap: The Tower of Power
y y′
x2 2x The power goes down by
x 3
3x2 one in each deriva ve
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

69. Recap: The Tower of Power
y y′
x2 2x The power goes down by
x 3
3x2 one in each deriva ve
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

70. Recap: The Tower of Power
y y′
x2 2x The power goes down by
x 3
3x2 one in each deriva ve
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

71. Recap: The Tower of Power
y y′
x2 2x The power goes down by
x 3
3x2 one in each deriva ve
1 −1/2
x1/2 2x
1 −2/3
x1/3 3x
2 −1/3
x2/3 3x

72. Recap: The Tower of Power
y y′
x2 2x The power goes down by
x 3
3x2 one in each deriva ve
1 −1/2 The coefficient in the
x1/2 2x deriva ve is the power of
1 −2/3
x1/3 3x
the original func on
2 −1/3
x2/3 3x

73. The Power Rule
There is moun ng evidence for
Theorem (The Power Rule)
Let r be a real number and f(x) = xr . Then
f′ (x) = rxr−1
as long as the expression on the right-hand side is defined.
Perhaps the most famous rule in calculus
We will assume it as of today
We will prove it many ways for many different r.

74. The other Tower of Power

75. Outline
Deriva ves so far
Deriva ves of power func ons by hand
The Power Rule
Deriva ves of polynomials
The Power Rule for whole number powers
The Power Rule for constants
The Sum Rule
The Constant Mul ple Rule
Deriva ves of sine and cosine

76. Remember your algebra
Fact
Let n be a posi ve whole number. Then
(x + h)n = xn + nxn−1 h + (stuff with at least two hs in it)

77. Remember your algebra
Fact
Let n be a posi ve whole number. Then
(x + h)n = xn + nxn−1 h + (stuff with at least two hs in it)
Proof.
We have
∑
n
(x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) =
n
ck xk hn−k
n copies k=0

78. Remember your algebra
Fact
Let n be a posi ve whole number. Then
(x + h)n = xn + nxn−1 h + (stuff with at least two hs in it)
Proof.
We have
∑
n
(x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) =
n
ck xk hn−k
n copies k=0

79. Remember your algebra
Fact
Let n be a posi ve whole number. Then
(x + h)n = xn + nxn−1 h + (stuff with at least two hs in it)
Proof.
We have
∑
n
(x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) =
n
ck xk hn−k
n copies k=0

80. Remember your algebra
Fact
Let n be a posi ve whole number. Then
(x + h)n = xn + nxn−1 h + (stuff with at least two hs in it)
Proof.
We have
∑
n
(x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) =
n
ck xk hn−k
n copies k=0

81. Remember your algebra
Fact
Let n be a posi ve whole number. Then
(x + h)n = xn + nxn−1 h + (stuff with at least two hs in it)
Proof.
We have
∑
n
(x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) =
n
ck xk hn−k
n copies k=0

82. Remember your algebra
Fact
Let n be a posi ve whole number. Then
(x + h)n = xn + nxn−1 h + (stuff with at least two hs in it)
Proof.
We have
∑
n
(x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) =
n
ck xk hn−k
n copies k=0

83. Pascal’s Triangle
.
1
1 1
1 2 1
1 3 3 1 (x + h)0 = 1
1 4 6 4 1 (x + h)1 = 1x + 1h
(x + h)2 = 1x2 + 2xh + 1h2
1 5 10 10 5 1
(x + h)3 = 1x3 + 3x2 h + 3xh2 + 1h3
1 6 15 20 15 6 1 ... ...

84. Pascal’s Triangle
.
1
1 1
1 2 1
1 3 3 1 (x + h)0 = 1
1 4 6 4 1 (x + h)1 = 1x + 1h
(x + h)2 = 1x2 + 2xh + 1h2
1 5 10 10 5 1
(x + h)3 = 1x3 + 3x2 h + 3xh2 + 1h3
1 6 15 20 15 6 1 ... ...

85. Pascal’s Triangle
.
1
1 1
1 2 1
1 3 3 1 (x + h)0 = 1
1 4 6 4 1 (x + h)1 = 1x + 1h
(x + h)2 = 1x2 + 2xh + 1h2
1 5 10 10 5 1
(x + h)3 = 1x3 + 3x2 h + 3xh2 + 1h3
1 6 15 20 15 6 1 ... ...

86. Pascal’s Triangle
.
1
1 1
1 2 1
1 3 3 1 (x + h)0 = 1
1 4 6 4 1 (x + h)1 = 1x + 1h
(x + h)2 = 1x2 + 2xh + 1h2
1 5 10 10 5 1
(x + h)3 = 1x3 + 3x2 h + 3xh2 + 1h3
1 6 15 20 15 6 1 ... ...

87. Proving the Power Rule
Theorem (The Power Rule)
d n
Let n be a posi ve whole number. Then x = nxn−1 .
dx

88. Proving the Power Rule
Theorem (The Power Rule)
d n
Let n be a posi ve whole number. Then x = nxn−1 .
dx
Proof.
As we showed above,
(x + h)n = xn + nxn−1 h + (stuff with at least two hs in it)
(x + h)n − xn nxn−1 h + (stuff with at least two hs in it)
So =
h h
= nxn−1 + (stuff with at least one h in it)
and this tends to nxn−1 as h → 0.

89. The Power Rule for constants?
Theorem
d
Let c be a constant. Then c=0
dx

90. The Power Rule for constants?
d 0
Theorem like x = 0x−1
d dx
Let c be a constant. Then c = 0.
.
dx

91. The Power Rule for constants?
d 0
Theorem like x = 0x−1
d dx
Let c be a constant. Then c = 0.
.
dx
Proof.
Let f(x) = c. Then
f(x + h) − f(x) c − c
= =0
h h
So f′ (x) = lim 0 = 0.
h→0

92. .
Calculus

93. Recall the Limit Laws
Fact
Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = L + M
x→a
2. lim [f(x) − g(x)] = L − M
x→a
3. lim [cf(x)] = cL
x→a
4. . . .

94. Adding functions
Theorem (The Sum Rule)
Let f and g be func ons and define
(f + g)(x) = f(x) + g(x)
Then if f and g are differen able at x, then so is f + g and
(f + g)′ (x) = f′ (x) + g′ (x).
Succinctly, (f + g)′ = f′ + g′ .

95. Proof of the Sum Rule
Proof.
Follow your nose:
(f + g)(x + h) − (f + g)(x)
(f + g)′ (x) = lim
h→0 h

96. Proof of the Sum Rule
Proof.
Follow your nose:
(f + g)(x + h) − (f + g)(x)
(f + g)′ (x) = lim
h→0 h
f(x + h) + g(x + h) − [f(x) + g(x)]
= lim
h→0 h

97. Proof of the Sum Rule
Proof.
Follow your nose:
(f + g)(x + h) − (f + g)(x)
(f + g)′ (x) = lim
h→0 h
f(x + h) + g(x + h) − [f(x) + g(x)]
= lim
h→0 h
f(x + h) − f(x) g(x + h) − g(x)
= lim + lim
h→0 h h→0 h

98. Proof of the Sum Rule
Proof.
Follow your nose:
(f + g)(x + h) − (f + g)(x)
(f + g)′ (x) = lim
h→0 h
f(x + h) + g(x + h) − [f(x) + g(x)]
= lim
h→0 h
f(x + h) − f(x) g(x + h) − g(x)
= lim + lim
h→0 h h→0 h
′ ′
= f (x) + g (x)

99. Scaling functions
Theorem (The Constant Mul ple Rule)
Let f be a func on and c a constant. Define
(cf)(x) = cf(x)
Then if f is differen able at x, so is cf and
(cf)′ (x) = c · f′ (x)
Succinctly, (cf)′ = cf′ .

100. Proof of Constant Multiple Rule
Proof.
Again, follow your nose.
(cf)(x + h) − (cf)(x)
(cf)′ (x) = lim
h→0 h

101. Proof of Constant Multiple Rule
Proof.
Again, follow your nose.
(cf)(x + h) − (cf)(x) cf(x + h) − cf(x)
(cf)′ (x) = lim = lim
h→0 h h→0 h

102. Proof of Constant Multiple Rule
Proof.
Again, follow your nose.
(cf)(x + h) − (cf)(x) cf(x + h) − cf(x)
(cf)′ (x) = lim = lim
h→0 h h→0 h
f(x + h) − f(x)
= c lim
h→0 h

103. Proof of Constant Multiple Rule
Proof.
Again, follow your nose.
(cf)(x + h) − (cf)(x) cf(x + h) − cf(x)
(cf)′ (x) = lim = lim
h→0 h h→0 h
f(x + h) − f(x)
= c lim = c · f′ (x)
h→0 h

104. Derivatives of polynomials
Example
d ( 3 )
Find 2x + x4 − 17x12 + 37
dx

105. Derivatives of polynomials
Example
d ( 3 )
Find 2x + x4 − 17x12 + 37
dx
Solu on
d ( 3 ) d ( 3) d d ( ) d
2x + x4 − 17x12 + 37 = 2x + x4 + −17x12 + (37)
dx dx dx dx dx

106. Derivatives of polynomials
Example
d ( 3 )
Find 2x + x4 − 17x12 + 37
dx
Solu on
d ( 3 ) d ( 3) d d ( ) d
2x + x4 − 17x12 + 37 = 2x + x4 + −17x12 + (37)
dx dx dx dx dx
d d d
= 2 x3 + x4 − 17 x12 + 0
dx dx dx

107. Derivatives of polynomials
Example
d ( 3 )
Find 2x + x4 − 17x12 + 37
dx
Solu on
d ( 3 ) d ( 3) d d ( ) d
2x + x4 − 17x12 + 37 = 2x + x4 + −17x12 + (37)
dx dx dx dx dx
d d d
= 2 x3 + x4 − 17 x12 + 0
dx dx dx
= 2 · 3x + 4x − 17 · 12x11
2 3

108. Derivatives of polynomials
Example
d ( 3 )
Find 2x + x4 − 17x12 + 37
dx
Solu on
d ( 3 ) d ( 3) d d ( ) d
2x + x4 − 17x12 + 37 = 2x + x4 + −17x12 + (37)
dx dx dx dx dx
d d d
= 2 x3 + x4 − 17 x12 + 0
dx dx dx
= 2 · 3x + 4x − 17 · 12x11
2 3
= 6x2 + 4x3 − 204x11

109. Outline
Deriva ves so far
Deriva ves of power func ons by hand
The Power Rule
Deriva ves of polynomials
The Power Rule for whole number powers
The Power Rule for constants
The Sum Rule
The Constant Mul ple Rule
Deriva ves of sine and cosine

110. Derivatives of Sine and Cosine
Fact
d
sin x = ???
dx
Proof.
From the defini on:

111. Derivatives of Sine and Cosine
Fact
d
sin x = ???
dx
Proof.
From the defini on:
d sin(x + h) − sin x
sin x = lim
dx h→0 h

112. Angle addition formulas
See Appendix A
sin(A + B) = . A cos B + cos A sin B
sin
cos(A + B) = cos A cos B − sin A sin B

113. Derivatives of Sine and Cosine
Fact
d
sin x = ???
dx
Proof.
From the defini on:
d sin(x + h) − sin x ( sin x cos h + cos x sin h) − sin x
sin x = lim = lim
dx h→0 h h→0 h

114. Derivatives of Sine and Cosine
Fact
d
sin x = ???
dx
Proof.
From the defini on:
d sin(x + h) − sin x ( sin x cos h + cos x sin h) − sin x
sin x = lim = lim
dx h→0 h h→0 h
cos h − 1 sin h
= sin x · lim + cos x · lim
h→0 h h→0 h

115. Two important trigonometric
limits
See Section 1.4
sin θ
lim . =1
θ→0 θ
cos θ − 1
sin θ θ lim =0
θ θ→0 θ
.
1 − cos θ 1

116. Derivatives of Sine and Cosine
Fact
d
sin x = ???
dx
Proof.
From the defini on:
d sin(x + h) − sin x ( sin x cos h + cos x sin h) − sin x
sin x = lim = lim
dx h→0 h h→0 h
cos h − 1 sin h
= sin x · lim + cos x · lim
h→0 h h→0 h
= sin x · 0 + cos x · 1

117. Derivatives of Sine and Cosine
Fact
d
sin x = ???
dx
Proof.
From the defini on:
d sin(x + h) − sin x ( sin x cos h + cos x sin h) − sin x
sin x = lim = lim
dx h→0 h h→0 h
cos h − 1 sin h
= sin x · lim + cos x · lim
h→0 h h→0 h
= sin x · 0 + cos x · 1

118. Derivatives of Sine and Cosine
Fact
d
sin x = cos x
dx
Proof.
From the defini on:
d sin(x + h) − sin x ( sin x cos h + cos x sin h) − sin x
sin x = lim = lim
dx h→0 h h→0 h
cos h − 1 sin h
= sin x · lim + cos x · lim
h→0 h h→0 h
= sin x · 0 + cos x · 1 = cos x

119. Illustration of Sine and Cosine
y
. x
π −π 0 π π
2 2
sin x

120. Illustration of Sine and Cosine
y
. x
π −π 0 π π cos x
2 2
sin x
f(x) = sin x has horizontal tangents where f′ = cos(x) is zero.

121. Illustration of Sine and Cosine
y
. x
π −π 0 π π cos x
2 2
sin x
f(x) = sin x has horizontal tangents where f′ = cos(x) is zero.
what happens at the horizontal tangents of cos?

122. Derivative of Cosine
Fact
d
cos x = − sin x
dx

123. Derivative of Cosine
Fact
d
cos x = − sin x
dx
Proof.
We already did the first. The second is similar (muta s mutandis):
d cos(x + h) − cos x
cos x = lim
dx h→0 h

124. Derivative of Cosine
Fact
d
cos x = − sin x
dx
Proof.
We already did the first. The second is similar (muta s mutandis):
d cos(x + h) − cos x (cos x cos h − sin x sin h) − cos x
cos x = lim = lim
dx h→0 h h→0 h

125. Derivative of Cosine
Fact
d
cos x = − sin x
dx
Proof.
We already did the first. The second is similar (muta s mutandis):
d cos(x + h) − cos x (cos x cos h − sin x sin h) − cos x
cos x = lim = lim
dx h→0 h h→0 h
cos h − 1 sin h
= cos x · lim − sin x · lim
h→0 h h→0 h

126. Derivative of Cosine
Fact
d
cos x = − sin x
dx
Proof.
We already did the first. The second is similar (muta s mutandis):
d cos(x + h) − cos x (cos x cos h − sin x sin h) − cos x
cos x = lim = lim
dx h→0 h h→0 h
cos h − 1 sin h
= cos x · lim − sin x · lim
h→0 h h→0 h
= cos x · 0 − sin x · 1 = − sin x

127. Summary
What have we learned today?
The Power Rule

128. Summary
What have we learned today?
The Power Rule
The deriva ve of a sum is the sum of the deriva ves
The deriva ve of a constant mul ple of a func on is that
constant mul ple of the deriva ve

129. Summary
What have we learned today?
The Power Rule
The deriva ve of a sum is the sum of the deriva ves
The deriva ve of a constant mul ple of a func on is that
constant mul ple of the deriva ve
The deriva ve of sine is cosine
The deriva ve of cosine is the opposite of sine.