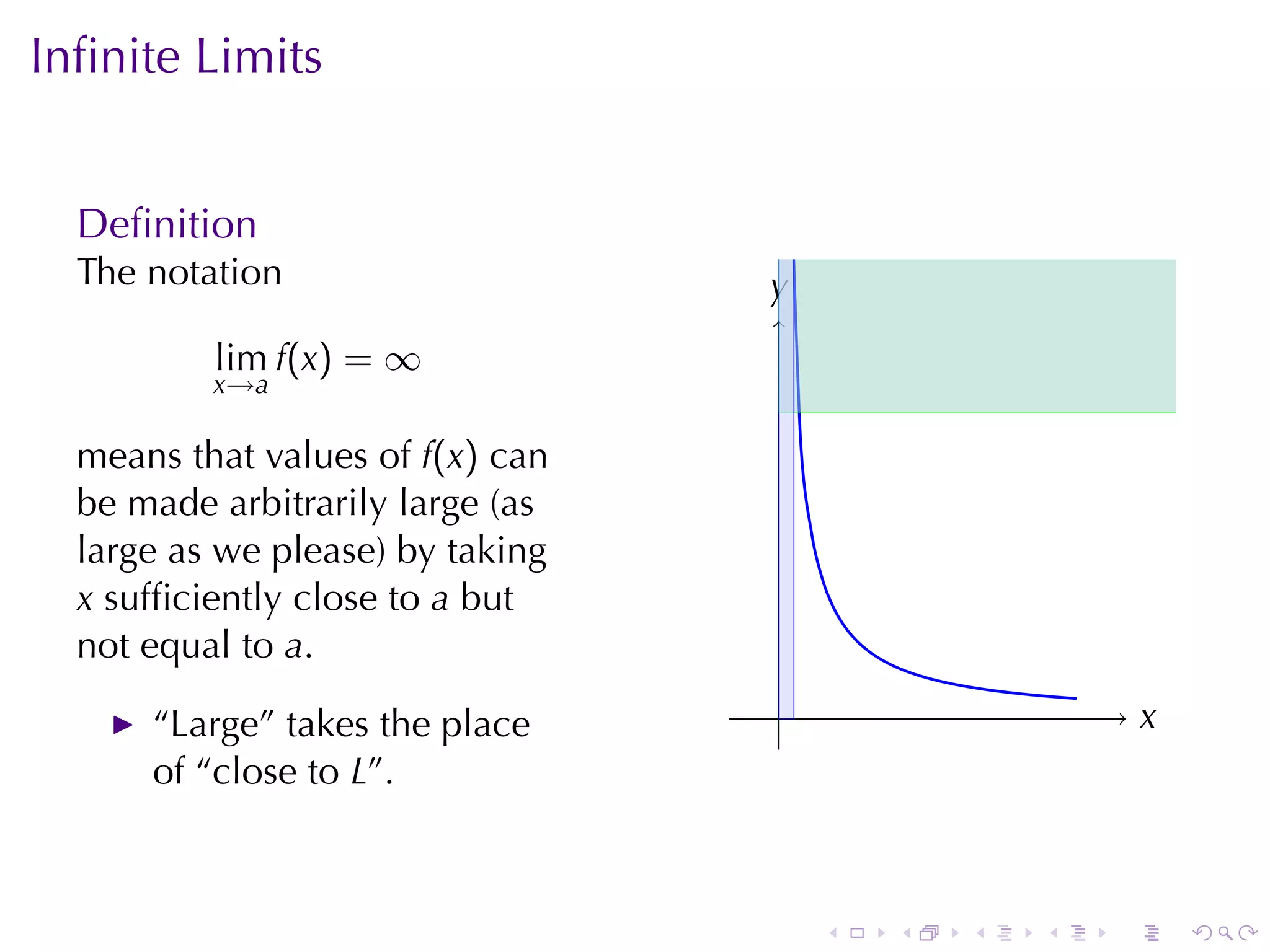
The document discusses limits involving infinity in calculus, explaining concepts such as function limits, vertical asymptotes, infinite limits, and indeterminate forms. It emphasizes definitions and notations for limits approaching infinity or negative infinity, as well as techniques for evaluating limits at points of discontinuity. Various examples and rules of thumb are provided to help understand how to evaluate limits in different scenarios.

1. Section 1.6
Limits involving Infinity
V63.0121.034, Calculus I
September 21, 2009
Announcements
Quiz 1 this week (§§1.1–1.3)
Written Assignment 2 due Wednesday
. . . . . .

2. Recall the definition of limit
Definition
We write
lim f(x) = L
x→a
and say
“the limit of f(x), as x approaches a, equals L”
if we can make the values of f(x) arbitrarily close to L (as close to
L as we like) by taking x to be sufficiently close to a (on either
side of a) but not equal to a.
. . . . . .

3. Recall the unboundedness problem
1
Recall why lim doesn’t exist.
x→0+ x
y
.
.? .
L
. x
.
No matter how thin we draw the strip to the right of x = 0, we
cannot “capture” the graph inside the box.
. . . . . .

4. Recall the unboundedness problem
1
Recall why lim doesn’t exist.
x→0+ x
y
.
.? .
L
. x
.
No matter how thin we draw the strip to the right of x = 0, we
cannot “capture” the graph inside the box.
. . . . . .

5. Recall the unboundedness problem
1
Recall why lim doesn’t exist.
x→0+ x
y
.
.? .
L
. x
.
No matter how thin we draw the strip to the right of x = 0, we
cannot “capture” the graph inside the box.
. . . . . .

6. Recall the unboundedness problem
1
Recall why lim doesn’t exist.
x→0+ x
y
.
.? .
L
. x
.
No matter how thin we draw the strip to the right of x = 0, we
cannot “capture” the graph inside the box.
. . . . . .

7. Outline
Infinite Limits
Vertical Asymptotes
Infinite Limits we Know
Limit “Laws” with Infinite Limits
Indeterminate Limit forms
Limits at ∞
Algebraic rates of growth
Rationalizing to get a limit
. . . . . .

8. Infinite Limits
Definition
The notation y
.
lim f(x) = ∞
x→a
means that values of f(x) can
be made arbitrarily large (as
large as we please) by taking
x sufficiently close to a but
not equal to a.
. x
.
. . . . . .

9. Infinite Limits
Definition
The notation y
.
lim f(x) = ∞
x→a
means that values of f(x) can
be made arbitrarily large (as
large as we please) by taking
x sufficiently close to a but
not equal to a.
“Large” takes the place . x
.
of “close to L”.
. . . . . .

10. Infinite Limits
Definition
The notation y
.
lim f(x) = ∞
x→a
means that values of f(x) can
be made arbitrarily large (as
large as we please) by taking
x sufficiently close to a but
not equal to a.
“Large” takes the place . x
.
of “close to L”.
. . . . . .

11. Infinite Limits
Definition
The notation y
.
lim f(x) = ∞
x→a
means that values of f(x) can
be made arbitrarily large (as
large as we please) by taking
x sufficiently close to a but
not equal to a.
“Large” takes the place . x
.
of “close to L”.
. . . . . .

12. Infinite Limits
Definition
The notation y
.
lim f(x) = ∞
x→a
means that values of f(x) can
be made arbitrarily large (as
large as we please) by taking
x sufficiently close to a but
not equal to a.
“Large” takes the place . x
.
of “close to L”.
. . . . . .

13. Infinite Limits
Definition
The notation y
.
lim f(x) = ∞
x→a
means that values of f(x) can
be made arbitrarily large (as
large as we please) by taking
x sufficiently close to a but
not equal to a.
“Large” takes the place . x
.
of “close to L”.
. . . . . .

14. Infinite Limits
Definition
The notation y
.
lim f(x) = ∞
x→a
means that values of f(x) can
be made arbitrarily large (as
large as we please) by taking
x sufficiently close to a but
not equal to a.
“Large” takes the place . x
.
of “close to L”.
. . . . . .

15. Infinite Limits
Definition
The notation y
.
lim f(x) = ∞
x→a
means that values of f(x) can
be made arbitrarily large (as
large as we please) by taking
x sufficiently close to a but
not equal to a.
“Large” takes the place . x
.
of “close to L”.
. . . . . .

16. Negative Infinity
Definition
The notation
lim f(x) = −∞
x→a
means that the values of f(x) can be made arbitrarily large
negative (as large as we please) by taking x sufficiently close to a
but not equal to a.
. . . . . .

17. Negative Infinity
Definition
The notation
lim f(x) = −∞
x→a
means that the values of f(x) can be made arbitrarily large
negative (as large as we please) by taking x sufficiently close to a
but not equal to a.
We call a number large or small based on its absolute value.
So −1, 000, 000 is a large (negative) number.
. . . . . .

18. Vertical Asymptotes
Definition
The line x = a is called a vertical asymptote of the curve y = f(x)
if at least one of the following is true:
lim f(x) = ∞ lim f(x) = −∞
x→a x→a
lim f(x) = ∞ lim f(x) = −∞
x→a+ x→a+
lim f(x) = ∞ lim f(x) = −∞
x→a− x→a−
. . . . . .

19. Infinite Limits we Know
y
.
.
.
1
lim
+ x
=∞
x→0 .
. . . . . . . x
.
.
.
.
. . . . . .

20. Infinite Limits we Know
y
.
.
.
1
lim
+ x
=∞
x→0 .
1
lim = −∞
x→0− x . . . . . . . x
.
.
.
.
. . . . . .

21. Infinite Limits we Know
y
.
.
.
1
lim
+ x
=∞
x→0 .
1
lim = −∞
x→0− x . . . . . . . x
.
1
lim =∞
x→0 x2 .
.
.
. . . . . .

22. Finding limits at trouble spots
Example
Let
x2 + 2
f (x ) =
x2 − 3x + 2
Find lim f(x) and lim f(x) for each a at which f is not
x→a− x→a+
continuous.
. . . . . .

23. Finding limits at trouble spots
Example
Let
x2 + 2
f (x ) =
x2 − 3x + 2
Find lim f(x) and lim f(x) for each a at which f is not
x→a− x→a+
continuous.
Solution
The denominator factors as (x − 1)(x − 2). We can record the
signs of the factors on the number line.
. . . . . .

24. Use the number line
−
.. 0
.. .
+
. x − 1)
(
1
.
. . . . . .

25. Use the number line
−
.. 0
.. .
+
. x − 1)
(
1
.
−
. 0
.. .
+
. x − 2)
(
2
.
. . . . . .

26. Use the number line
−
.. 0
.. .
+
. x − 1)
(
1
.
−
. 0
.. .
+
. x − 2)
(
2
.
.
+
. x2 + 2 )
(
. . . . . .

27. Use the number line
−
.. 0
.. .
+
. x − 1)
(
1
.
−
. 0
.. .
+
. x − 2)
(
2
.
.
+
. x2 + 2 )
(
. . f
.(x)
1
. 2
.
. . . . . .

28. Use the number line
−
.. 0
.. .
+
. x − 1)
(
1
.
−
. 0
.. .
+
. x − 2)
(
2
.
.
+
. x2 + 2 )
(
.
+ . . f
.(x)
1
. 2
.
. . . . . .

29. Use the number line
−
.. 0
.. .
+
. x − 1)
(
1
.
−
. 0
.. .
+
. x − 2)
(
2
.
.
+
. x2 + 2 )
(
.
+ ±.
. ∞ . f
.(x)
1
. 2
.
. . . . . .

30. Use the number line
−
.. 0
.. .
+
. x − 1)
(
1
.
−
. 0
.. .
+
. x − 2)
(
2
.
.
+
. x2 + 2 )
(
.
+ ±. −
. ∞ . . f
.(x)
1
. 2
.
. . . . . .

31. Use the number line
−
.. 0
.. .
+
. x − 1)
(
1
.
−
. 0
.. .
+
. x − 2)
(
2
.
.
+
. x2 + 2 )
(
.
+ ±. −
. ∞ . . ∞. f
.(x)
1
. 2
.
. . . . . .

32. Use the number line
−
.. 0
.. .
+
. x − 1)
(
1
.
−
. 0
.. .
+
. x − 2)
(
2
.
.
+
. x2 + 2 )
(
.
+ ±. −
. ∞ . . ∞. .
+
f
.(x)
1
. 2
.
. . . . . .

33. Use the number line
−
.. 0
.. .
+
. x − 1)
(
1
.
−
. 0
.. .
+
. x − 2)
(
2
.
.
+
. x2 + 2 )
(
.
+ ±. −
. ∞ . . ∞. .
+
f
.(x)
1
. 2
.
So
lim f(x) = +∞ lim f(x) = −∞
x→1− x→2−
lim f(x) = −∞ lim f(x) = +∞
x→1+ x→2+
. . . . . .

34. In English, now
To explain the limit, you can say:
“As x → 1− , the numerator approaches 2, and the denominator
approaches 0 while remaining positive. So the limit is +∞.”
. . . . . .

35. The graph so far
y
.
. . . . . .
x
−
. 1 1
. 2
. 3
.
. . . . . .

36. The graph so far
y
.
. . . . . .
x
−
. 1 1
. 2
. 3
.
. . . . . .

37. The graph so far
y
.
. . . . . .
x
−
. 1 1
. 2
. 3
.
. . . . . .

38. The graph so far
y
.
. . . . . .
x
−
. 1 1
. 2
. 3
.
. . . . . .

39. The graph so far
y
.
. . . . . .
x
−
. 1 1
. 2
. 3
.
. . . . . .

40. Limit Laws (?) with infinite limits
If lim f(x) = ∞ and lim g(x) = ∞, then lim (f(x) + g(x)) = ∞.
x→a x→a x→a
That is,
∞ .
. +∞=∞
If lim f(x) = −∞ and lim g(x) = −∞, then
x→a x→a
lim (f(x) + g(x)) = −∞. That is,
x→a
− .
. ∞ − ∞ = −∞
. . . . . .

41. Rules of Thumb with infinite limits
If lim f(x) = ∞ and lim g(x) = ∞, then lim (f(x) + g(x)) = ∞.
x→a x→a x→a
That is,
∞ .
. +∞=∞
If lim f(x) = −∞ and lim g(x) = −∞, then
x→a x→a
lim (f(x) + g(x)) = −∞. That is,
x→a
− .
. ∞ − ∞ = −∞
. . . . . .

42. Rules of Thumb with infinite limits
If lim f(x) = L and lim g(x) = ±∞, then
x→a x→a
lim (f(x) + g(x)) = ±∞. That is,
x→a
L+∞=∞
. .
L − ∞ = −∞
. . . . . .

43. Rules of Thumb with infinite limits
Kids, don’t try this at home!
The product of a finite limit and an infinite limit is infinite if
the finite limit is not 0.
{
∞. if L > 0
. ·∞=
L
−∞ if L < 0.
{
−∞ if L > 0
. · (−∞) = .
L
∞ if L < 0.
. . . . . .

44. Multiplying infinite limits
Kids, don’t try this at home!
The product of two infinite limits is infinite.
∞·∞=∞
. .
∞ · (−∞) = −∞
(−∞) · (−∞) = ∞
. . . . . .

45. Dividing by Infinity
Kids, don’t try this at home!
The quotient of a finite limit by an infinite limit is zero:
L .
. =0
∞
. . . . . .

46. Dividing by zero is still not allowed
1 .
. =∞
0
There are examples of such limit forms where the limit is ∞, −∞,
undecided between the two, or truly neither.
. . . . . .

47. Indeterminate Limit forms
L
Limits of the form are indeterminate. There is no rule for
0
evaluating such a form; the limit must be examined more closely.
Consider these:
1 −1
lim =∞ lim = −∞
x→0 x2 x→0 x2
1 1
lim
+ x
=∞ lim = −∞
x→0 x→0 − x
1 L
Worst, lim is of the form , but the limit does not
x→0 x sin(1/x) 0
exist, even in the left- or right-hand sense. There are infinitely
many vertical asymptotes arbitrarily close to 0!
. . . . . .

48. Indeterminate Limit forms
Limits of the form 0 · ∞ and ∞ − ∞ are also indeterminate.
Example
1
The limit lim sin x · is of the form 0 · ∞, but the answer is
x→0+ x
1.
1
The limit lim sin2 x · is of the form 0 · ∞, but the answer is
x→0+ x
0.
1
The limit lim sin x · 2 is of the form 0 · ∞, but the answer is
x→0 + x
∞.
Limits of indeterminate forms may or may not “exist.” It will
depend on the context.
. . . . . .

49. Indeterminate forms are like Tug Of War
Which side wins depends on which side is stronger.
. . . . . .

50. Outline
Infinite Limits
Vertical Asymptotes
Infinite Limits we Know
Limit “Laws” with Infinite Limits
Indeterminate Limit forms
Limits at ∞
Algebraic rates of growth
Rationalizing to get a limit
. . . . . .

51. Definition
Let f be a function defined on some interval (a, ∞). Then
lim f(x) = L
x→∞
means that the values of f(x) can be made as close to L as we
like, by taking x sufficiently large.
. . . . . .

52. Definition
Let f be a function defined on some interval (a, ∞). Then
lim f(x) = L
x→∞
means that the values of f(x) can be made as close to L as we
like, by taking x sufficiently large.
Definition
The line y = L is a called a horizontal asymptote of the curve
y = f(x) if either
lim f(x) = L or lim f(x) = L.
x→∞ x→−∞
. . . . . .

53. Definition
Let f be a function defined on some interval (a, ∞). Then
lim f(x) = L
x→∞
means that the values of f(x) can be made as close to L as we
like, by taking x sufficiently large.
Definition
The line y = L is a called a horizontal asymptote of the curve
y = f(x) if either
lim f(x) = L or lim f(x) = L.
x→∞ x→−∞
y = L is a horizontal line!
. . . . . .

54. Basic limits at infinity
Theorem
Let n be a positive integer. Then
1
lim =0
x→∞ xn
1
lim n = 0
x→−∞ x
. . . . . .

55. Using the limit laws to compute limits at ∞
Example
Find
2x3 + 3x + 1
lim
x→∞ 4x3 + 5x2 + 7
if it exists.
A does not exist
B 1/2
C 0
D ∞
. . . . . .

56. Using the limit laws to compute limits at ∞
Example
Find
2x3 + 3x + 1
lim
x→∞ 4x3 + 5x2 + 7
if it exists.
A does not exist
B 1/2
C 0
D ∞
. . . . . .

57. Solution
Factor out the largest power of x from the numerator and
denominator. We have
2x3 + 3x + 1 x3 (2 + 3/x2 + 1/x3 )
= 3
4x3 + 5x2 + 7 x (4 + 5/x + 7/x3 )
2x3 + 3x + 1 2 + 3/x2 + 1/x3
lim = lim
x→∞ 4x3 + 5x2 + 7 x→∞ 4 + 5/x + 7/x3
2+0+0 1
= =
4+0+0 2
. . . . . .

58. Solution
Factor out the largest power of x from the numerator and
denominator. We have
2x3 + 3x + 1 x3 (2 + 3/x2 + 1/x3 )
= 3
4x3 + 5x2 + 7 x (4 + 5/x + 7/x3 )
2x3 + 3x + 1 2 + 3/x2 + 1/x3
lim = lim
x→∞ 4x3 + 5x2 + 7 x→∞ 4 + 5/x + 7/x3
2+0+0 1
= =
4+0+0 2
Upshot
When finding limits of algebraic expressions at infinity, look at
the highest degree terms.
. . . . . .

59. Another Example
Example
x
Find lim
x→∞ x2 +1
. . . . . .

60. Another Example
Example
x
Find lim
x→∞ x2 +1
Answer
The limit is 0.
. . . . . .

61. Solution
Again, factor out the largest power of x from the numerator and
denominator. We have
x x(1) 1 1
= 2 = ·
x2 + 1 x (1 + 1/x2 ) x 1 + 1/x2
x 1 1 1 1
lim = lim = lim · lim
x→∞ x2 + 1 x→∞ x 1 + 1/x2 x→∞ x x→∞ 1 + 1/x2
1
=0· = 0.
1+0
. . . . . .

62. Another Example
Example
x
Find lim
x→∞ x2 +1
Answer
The limit is 0.
y
.
. x
.
. . . . . .

63. Another Example
Example
x
Find lim
x→∞ x2 +1
Answer
The limit is 0.
y
.
. x
.
Notice that the graph does cross the asymptote, which
contradicts one of the heuristic definitions of asymptote.
. . . . . .

64. Solution
Again, factor out the largest power of x from the numerator and
denominator. We have
x x(1) 1 1
= 2 = ·
x2 + 1 x (1 + 1/x2 ) x 1 + 1/x2
x 1 1 1 1
lim = lim = lim · lim
x→∞ x2 + 1 x→∞ x 1 + 1/x2 x→∞ x x→∞ 1 + 1/x2
1
=0· = 0.
1+0
Remark
Had the higher power been in the numerator, the limit would
have been ∞.
. . . . . .

65. Another Example
Example
Find
√
3x4 + 7
lim
x→∞ x2 + 3
. . . . . .

66. Another Example
Example
Find
√ √ √
. 3x4 + 7 ∼ . 3x4 = 3x2
√
3x4 + 7
lim
x→∞ x2 + 3
Answer √
The limit is 3.
. . . . . .

67. Solution
√ √
3x4 + 7 x4 (3 + 7/x4 )
lim = lim 2
x→∞ x2 + 3 x→∞ x (1 + 3/x2 )
√
x2 (3 + 7/x4 )
= lim 2
x→∞ x (1 + 3/x2 )
√
(3 + 7/x4 )
= lim
x→∞ 1 + 3/x2
√
3+0 √
= = 3.
1+0
. . . . . .

68. Rationalizing to get a limit
Example (√ )
Compute lim 4x2 + 17 − 2x .
x→∞
. . . . . .

69. Rationalizing to get a limit
Example (√ )
Compute lim 4x2 + 17 − 2x .
x→∞
Solution
This limit is of the form ∞ − ∞, which we cannot use. So we
rationalize the numerator (the denominator is 1) to get an
expression that we can use the limit laws on.
(√ ) (√ ) √4x2 + 17 + 2x
lim 4x2 + 17 − 2x = lim 4x2 + 17 − 2x · √
x→∞ x→∞ 4x2 + 17 + 2x
(4x 2 + 17) − 4x2
= lim √
x→∞ 4x2 + 17 + 2x
17
= lim √ =0
x→∞ 4x 2 + 17 + 2x
. . . . . .

70. Summary
Infinity is a more complicated concept than a single number.
There are rules of thumb, but there are also exceptions.
Take a two-pronged approach to limits involving infinity:
Look at the expression to guess the limit.
Use limit rules and algebra to verify it.
. . . . . .