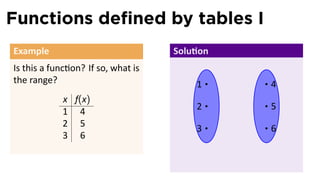
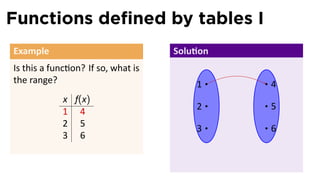
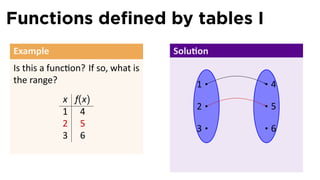
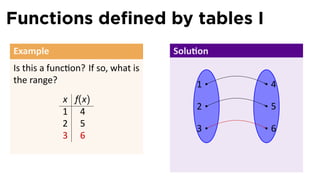
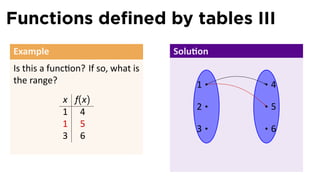
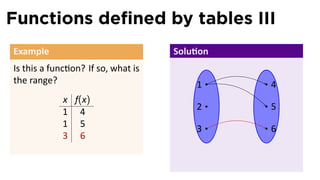
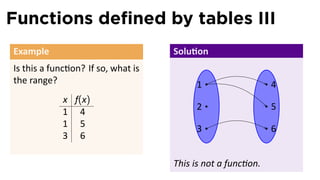
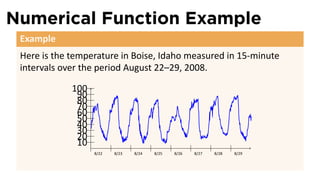
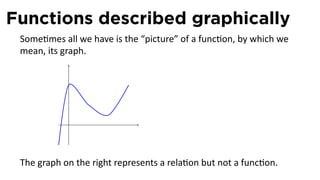
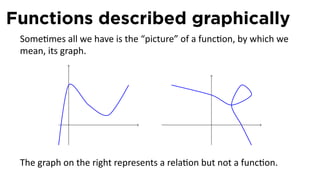
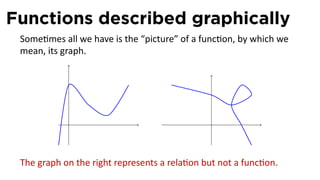
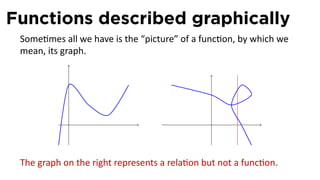
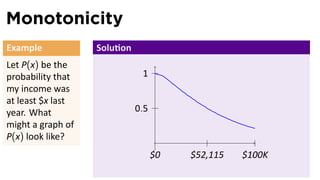
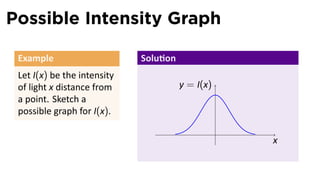
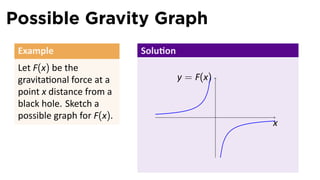
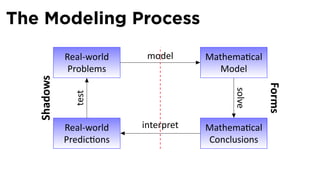
The document outlines the fundamentals of functions in calculus, including their definitions, representations, and properties. It discusses various ways to express functions, such as through formulas, numeric tables, graphs, and verbal descriptions, while also introducing the concepts of monotonicity and symmetry. The importance of functions in modeling real-world problems and their different types, such as piecewise-defined functions, is emphasized.



















![Piecewise-defined functions
Example Solu on
Let The domain is [0, 2]. The graph
{ can be drawn piecewise.
x2 0 ≤ x ≤ 1;
f(x) = 2
3−x 1 < x ≤ 2.
1
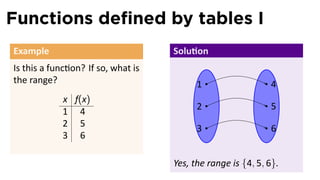
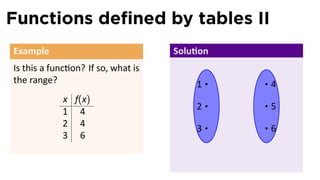
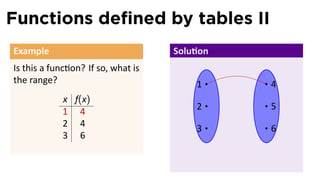
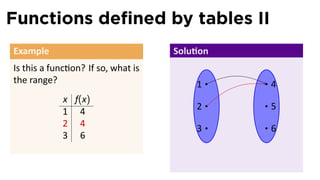
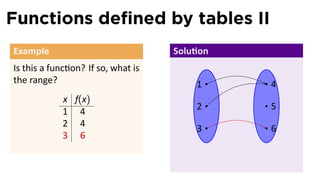
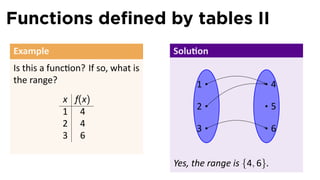
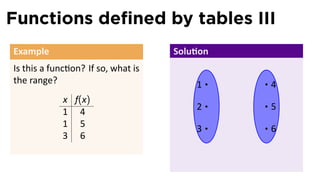
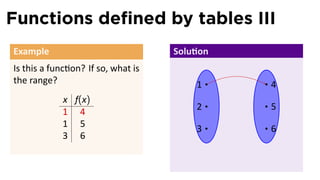
Find the domain and range of f
and graph the func on. .
0 1 2](https://image.slidesharecdn.com/lesson01-functions001slides-110124144728-phpapp02/85/Lesson-1-Functions-and-their-representations-slides-23-320.jpg)
![Piecewise-defined functions
Example Solu on
Let The domain is [0, 2]. The graph
{ can be drawn piecewise.
x2 0 ≤ x ≤ 1;
f(x) = 2
3−x 1 < x ≤ 2.
1
Find the domain and range of f
and graph the func on. .
0 1 2](https://image.slidesharecdn.com/lesson01-functions001slides-110124144728-phpapp02/85/Lesson-1-Functions-and-their-representations-slides-24-320.jpg)
![Piecewise-defined functions
Example Solu on
Let The domain is [0, 2]. The graph
{ can be drawn piecewise.
x2 0 ≤ x ≤ 1;
f(x) = 2
3−x 1 < x ≤ 2.
1
Find the domain and range of f
and graph the func on. .
0 1 2](https://image.slidesharecdn.com/lesson01-functions001slides-110124144728-phpapp02/85/Lesson-1-Functions-and-their-representations-slides-25-320.jpg)
![Piecewise-defined functions
Example Solu on
Let The domain is [0, 2]. The graph
{ can be drawn piecewise.
x2 0 ≤ x ≤ 1;
f(x) = 2
3−x 1 < x ≤ 2.
1
Find the domain and range of f
and graph the func on. .
0 1 2
The range is [0, 2).](https://image.slidesharecdn.com/lesson01-functions001slides-110124144728-phpapp02/85/Lesson-1-Functions-and-their-representations-slides-26-320.jpg)