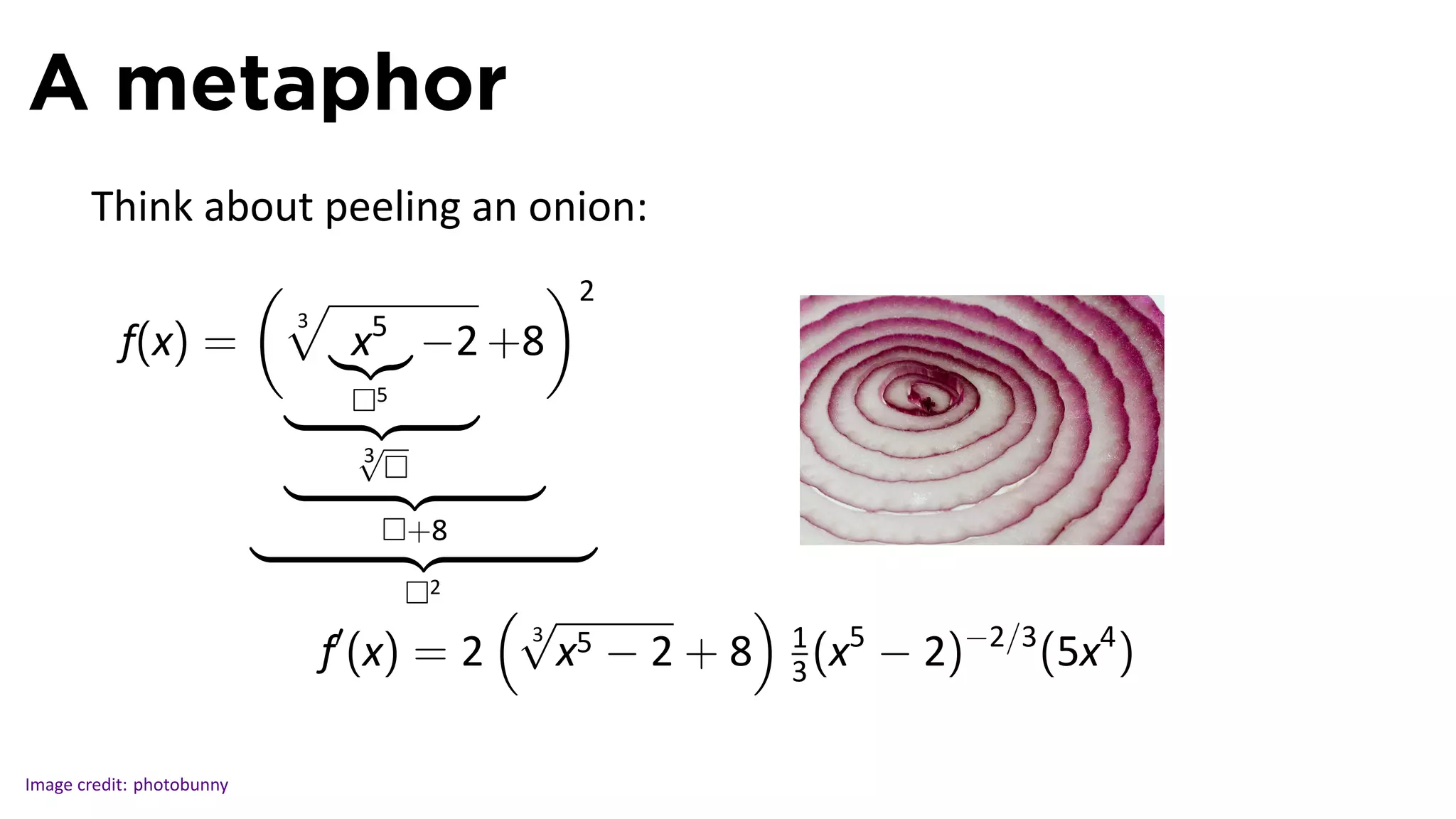
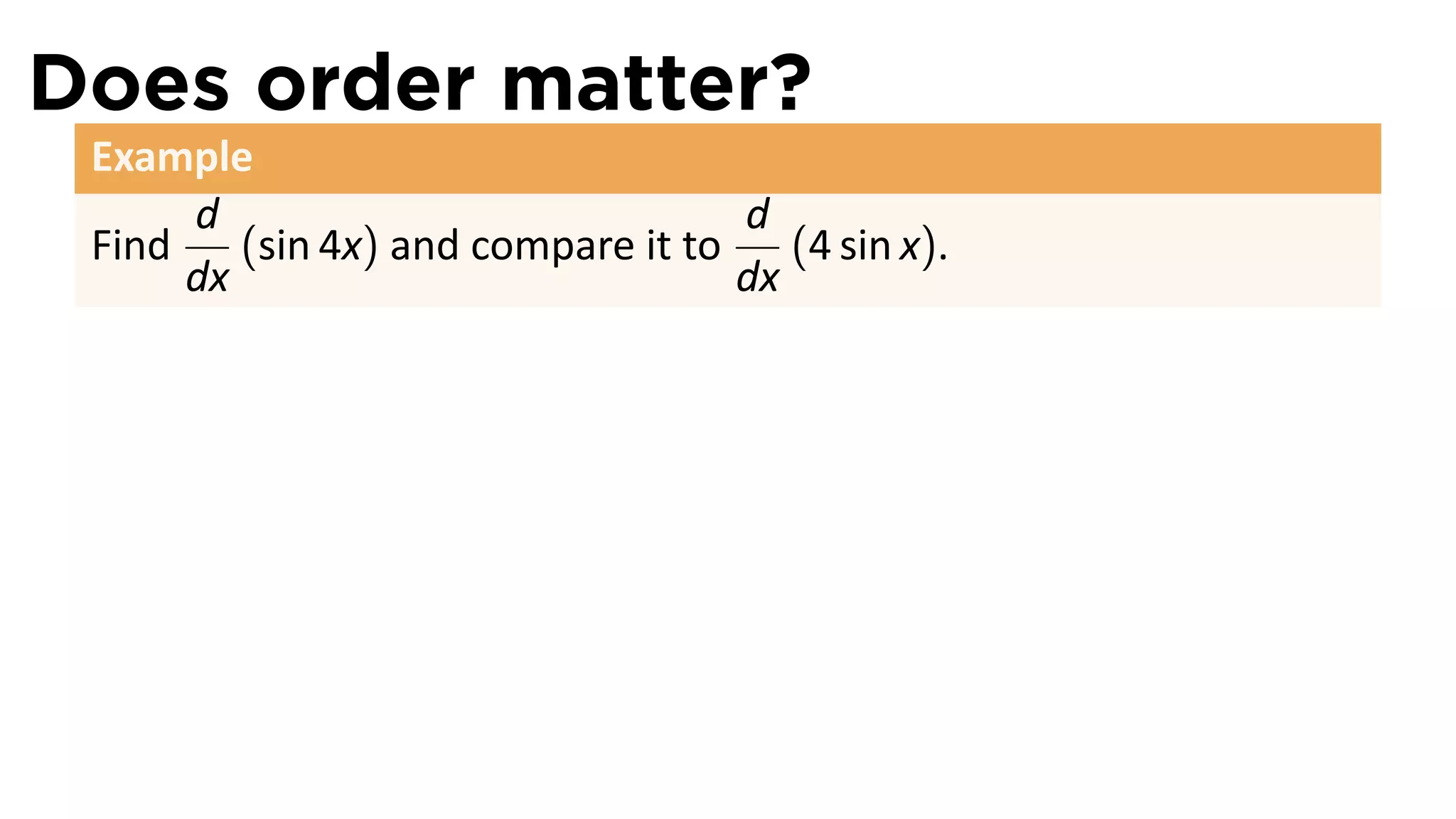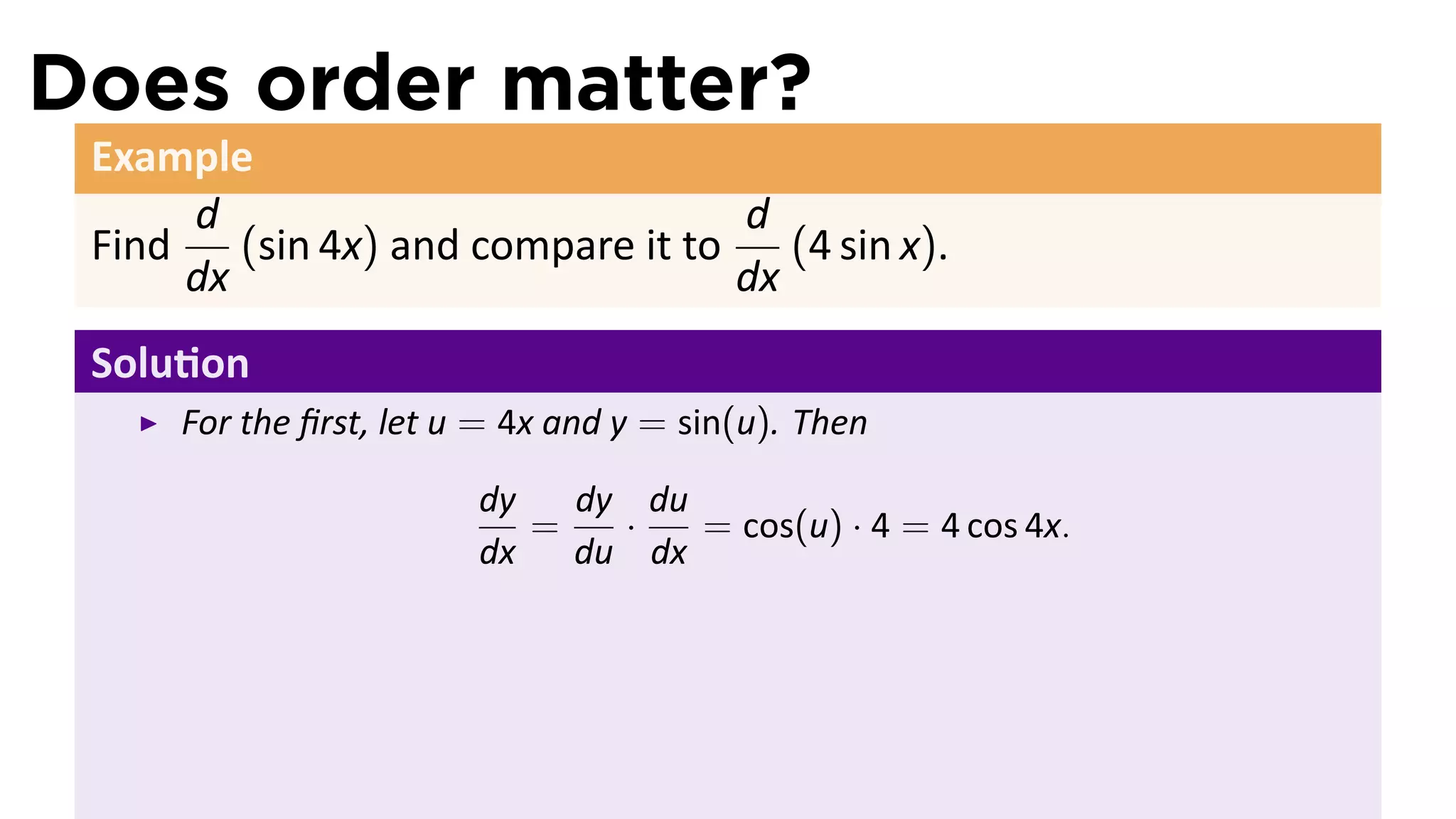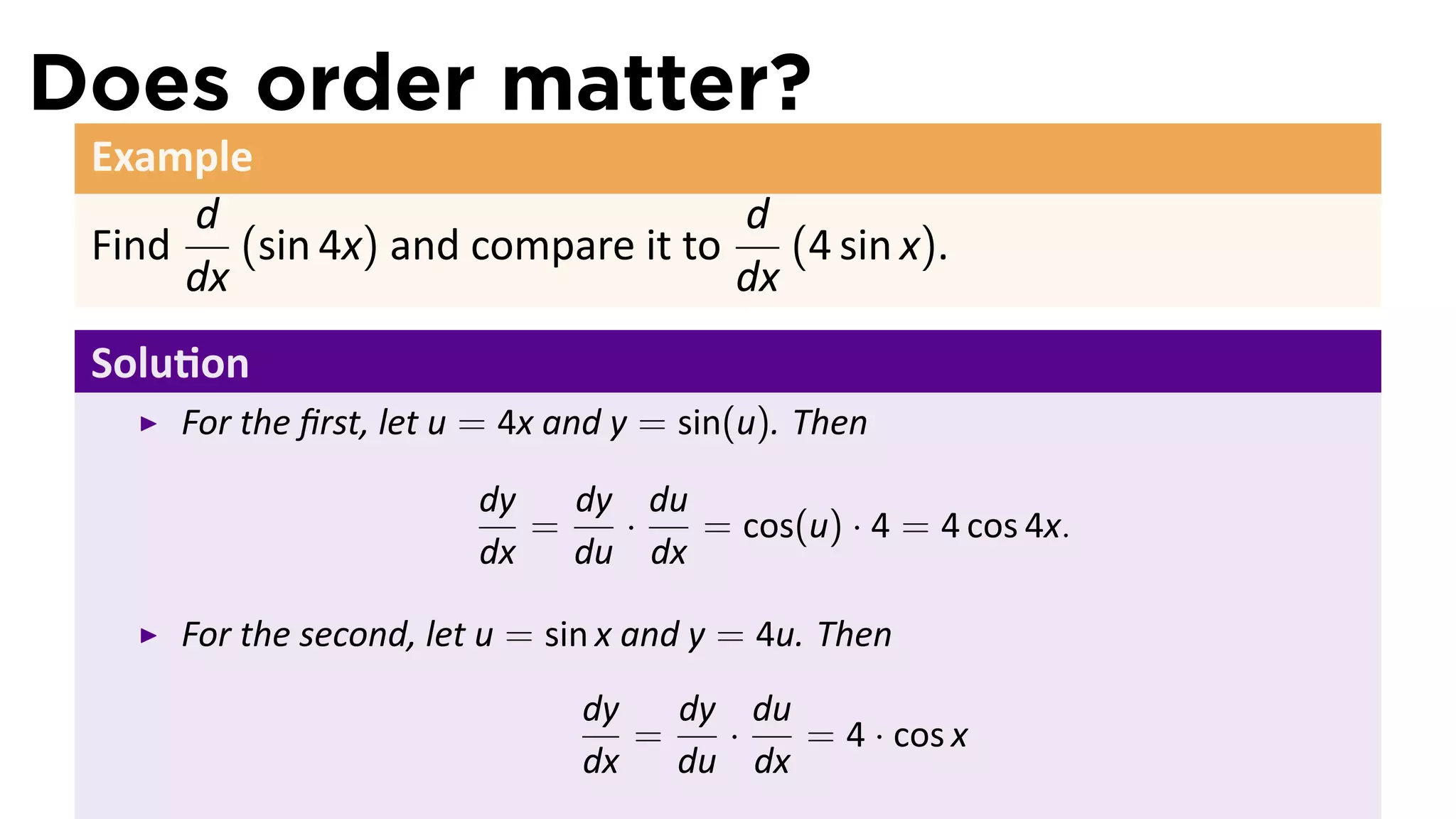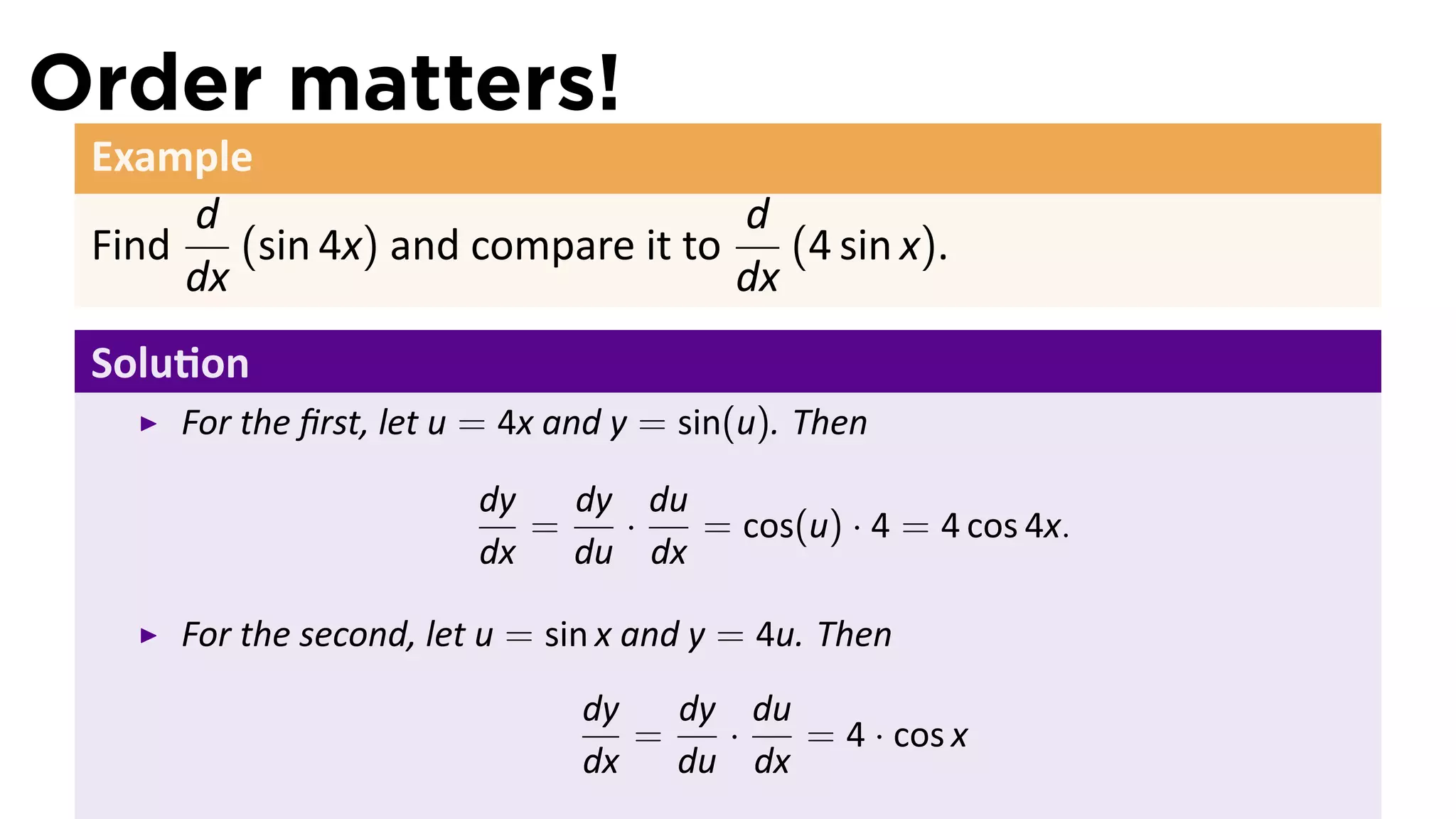The document discusses the chain rule in calculus, detailing its definition, applications, and examples for differentiating compositions of functions. It elaborates on the relationship between the derivatives of composite functions using both Newtonian and Leibnizian notations. The key theorem established is that if f and g are differentiable, then the derivative of the composition (f ◦ g)'(x) equals f'(g(x))g'(x).

1. Sec on 2.5
The Chain Rule
V63.0121.011: Calculus I
Professor Ma hew Leingang
New York University
February 23, 2011
.

2. Announcements
Quiz 2 next week on
§§1.5, 1.6, 2.1, 2.2
Midterm March 7 on all
sec ons in class (covers
all sec ons up to 2.5)

3. Objectives
Given a compound
expression, write it as a
composi on of func ons.
Understand and apply
the Chain Rule for the
deriva ve of a
composi on of func ons.
Understand and use
Newtonian and Leibnizian
nota ons for the Chain
Rule.

4. Compositions
See Section 1.2 for review
Defini on
If f and g are func ons, the composi on (f ◦ g)(x) = f(g(x)) means “do g first,
then f.”
.

5. Compositions
See Section 1.2 for review
Defini on
If f and g are func ons, the composi on (f ◦ g)(x) = f(g(x)) means “do g first,
then f.”
x g(x)
g .

6. Compositions
See Section 1.2 for review
Defini on
If f and g are func ons, the composi on (f ◦ g)(x) = f(g(x)) means “do g first,
then f.”
x g(x)
g . f

7. Compositions
See Section 1.2 for review
Defini on
If f and g are func ons, the composi on (f ◦ g)(x) = f(g(x)) means “do g first,
then f.”
x g(x) f(g(x))
g . f

8. Compositions
See Section 1.2 for review
Defini on
If f and g are func ons, the composi on (f ◦ g)(x) = f(g(x)) means “do g first,
then f.”
x
g
f g
g(x)
◦. f
f(g(x))

9. Compositions
See Section 1.2 for review
Defini on
If f and g are func ons, the composi on (f ◦ g)(x) = f(g(x)) means “do g first,
then f.”
x
g
f g
g(x)
◦. f
f(g(x))
Our goal for the day is to understand how the deriva ve of the composi on of
two func ons depends on the deriva ves of the individual func ons.

10. Outline
Heuris cs
Analogy
The Linear Case
The chain rule
Examples

11. Analogy
Think about riding a bike. To
go faster you can either:
.
Image credit: SpringSun

12. Analogy
Think about riding a bike. To
go faster you can either:
pedal faster
.
Image credit: SpringSun

13. Analogy
Think about riding a bike. To
go faster you can either:
pedal faster
change gears
.
Image credit: SpringSun

14. Analogy
Think about riding a bike. To
go faster you can either:
pedal faster
change gears
.
The angular posi on (φ) of the back wheel depends on the posi on
of the front sprocket (θ):
R..
θ
φ(θ) =
r..
Image credit: SpringSun

15. Analogy
Think about riding a bike. To
go faster you can either:
pedal faster
change gears
radius of front sprocket .
The angular posi on (φ) of the back wheel depends on the posi on
of the front sprocket (θ):
R..
θ
φ(θ) =
r..
Image credit: SpringSun radius of back sprocket

16. Analogy
Think about riding a bike. To
go faster you can either:
pedal faster
change gears
.
The angular posi on (φ) of the back wheel depends on the posi on
of the front sprocket (θ):
R..
θ
φ(θ) =
r..
And so the angular speed of the back wheel depends on the
Image credit: SpringSun ve of this func on and the speed of the front sprocket.
deriva

17. The Linear Case
Ques on
Let f(x) = mx + b and g(x) = m′ x + b′ . What can you say about the composi on?

18. The Linear Case
Ques on
Let f(x) = mx + b and g(x) = m′ x + b′ . What can you say about the composi on?
Answer
f(g(x)) = m(m′ x + b′ ) + b = (mm′ )x + (mb′ + b)

19. The Linear Case
Ques on
Let f(x) = mx + b and g(x) = m′ x + b′ . What can you say about the composi on?
Answer
f(g(x)) = m(m′ x + b′ ) + b = (mm′ )x + (mb′ + b)
The composi on is also linear

20. The Linear Case
Ques on
Let f(x) = mx + b and g(x) = m′ x + b′ . What can you say about the composi on?
Answer
f(g(x)) = m(m′ x + b′ ) + b = (mm′ )x + (mb′ + b)
The composi on is also linear
The slope of the composi on is the product of the slopes of the two
func ons.

21. The Linear Case
Ques on
Let f(x) = mx + b and g(x) = m′ x + b′ . What can you say about the composi on?
Answer
f(g(x)) = m(m′ x + b′ ) + b = (mm′ )x + (mb′ + b)
The composi on is also linear
The slope of the composi on is the product of the slopes of the two
func ons.
The deriva ve is supposed to be a local lineariza on of a func on. So there
should be an analog of this property in deriva ves.

22. The Nonlinear Case
Let u = g(x) and y = f(u). Suppose x is changed by a small amount
∆x. Then
∆y
f′ (u) ≈ =⇒ ∆y ≈ f′ (u)∆u
∆u
and
∆y
g′ (x) ≈ =⇒ ∆u ≈ g′ (x)∆x.
∆x
So
∆y
∆y ≈ f′ (u)g′ (x)∆x =⇒ ≈ f′ (u)g′ (x)
∆x

23. Outline
Heuris cs
Analogy
The Linear Case
The chain rule
Examples

24. Theorem of the day: The chain rule
Theorem
Let f and g be func ons, with g differen able at x and f differen able
at g(x). Then f ◦ g is differen able at x and
(f ◦ g)′ (x) = f′ (g(x))g′ (x)
In Leibnizian nota on, let y = f(u) and u = g(x). Then
dy dy du
=
dx du dx

25. Observations
Succinctly, the deriva ve of a
composi on is the product
of the deriva ves
.
Image credit: ooOJasonOoo

26. Theorem of the day: The chain rule
Theorem
Let f and g be func ons, with g differen able at x and f differen able
at g(x). Then f ◦ g is differen able at x and
(f ◦ g)′ (x) = f′ (g(x))g′ (x)
In Leibnizian nota on, let y = f(u) and u = g(x). Then
dy dy du
=
dx du dx

27. Observations
Succinctly, the deriva ve of a
composi on is the product
of the deriva ves
The only complica on is
where these deriva ves are
evaluated: at the same point
the func ons are
.
Image credit: ooOJasonOoo

28. Compositions
See Section 1.2 for review
Defini on
If f and g are func ons, the composi on (f ◦ g)(x) = f(g(x)) means “do g first,
then f.”
x
g
f g
g(x)
◦. f
f(g(x))

29. Observations
Succinctly, the deriva ve of a
composi on is the product
of the deriva ves
The only complica on is
where these deriva ves are
evaluated: at the same point
the func ons are
In Leibniz nota on, the Chain
Rule looks like cancella on of .
(fake) frac ons
Image credit: ooOJasonOoo

30. Theorem of the day: The chain rule
Theorem
Let f and g be func ons, with g differen able at x and f differen able
at g(x). Then f ◦ g is differen able at x and
(f ◦ g)′ (x) = f′ (g(x))g′ (x)
In Leibnizian nota on, let y = f(u) and u = g(x). Then
dy dy du
=
dx du dx

31. Theorem of the day: The chain rule
Theorem
Let f and g be func ons, with g differen able at x and f differen able
at g(x). Then f ◦ g is differen able at x and
(f ◦ g)′ (x) = f′ (g(x))g′ (x)
In Leibnizian nota on, let y = f(u) and u = g(x). Then
dy .du
dy dy du dx
du
=
dx du dx

32. Outline
Heuris cs
Analogy
The Linear Case
The chain rule
Examples

33. Example
Example
√
let h(x) = 3x2 + 1. Find h′ (x).

34. Example
Example
√
let h(x) = 3x2 + 1. Find h′ (x).
Solu on
First, write h as f ◦ g.

35. Example
Example
√
let h(x) = 3x2 + 1. Find h′ (x).
Solu on
√
First, write h as f ◦ g. Let f(u) = u and g(x) = 3x2 + 1.

36. Example
Example
√
let h(x) = 3x2 + 1. Find h′ (x).
Solu on
√
First, write h as f ◦ g. Let f(u) = u and g(x) = 3x2 + 1. Then
f′ (u) = 1 u−1/2 , and g′ (x) = 6x. So
2
h′ (x) = 1 u−1/2 (6x)
2

37. Example
Example
√
let h(x) = 3x2 + 1. Find h′ (x).
Solu on
√
First, write h as f ◦ g. Let f(u) = u and g(x) = 3x2 + 1. Then
f′ (u) = 1 u−1/2 , and g′ (x) = 6x. So
2
3x
h′ (x) = 1 u−1/2 (6x) = 1 (3x2 + 1)−1/2 (6x) = √
2 2
3x2 + 1

38. Corollary
Corollary (The Power Rule Combined with the Chain Rule)
If n is any real number and u = g(x) is differen able, then
d n du
(u ) = nun−1 .
dx dx

39. Does order matter?
Example
d d
Find (sin 4x) and compare it to (4 sin x).
dx dx

40. Does order matter?
Example
d d
Find (sin 4x) and compare it to (4 sin x).
dx dx
Solu on
For the first, let u = 4x and y = sin(u). Then
dy dy du
= · = cos(u) · 4 = 4 cos 4x.
dx du dx

41. Does order matter?
Example
d d
Find (sin 4x) and compare it to (4 sin x).
dx dx
Solu on
For the first, let u = 4x and y = sin(u). Then
dy dy du
= · = cos(u) · 4 = 4 cos 4x.
dx du dx
For the second, let u = sin x and y = 4u. Then
dy dy du
= · = 4 · cos x
dx du dx

42. Order matters!
Example
d d
Find (sin 4x) and compare it to (4 sin x).
dx dx
Solu on
For the first, let u = 4x and y = sin(u). Then
dy dy du
= · = cos(u) · 4 = 4 cos 4x.
dx du dx
For the second, let u = sin x and y = 4u. Then
dy dy du
= · = 4 · cos x
dx du dx

43. Example
(√ )2
x − 2 + 8 . Find f′ (x).
3 5
Let f(x) =

44. Example
(√ )2
x − 2 + 8 . Find f′ (x).
3 5
Let f(x) =
Solu on
d (√ 5 )2 (√ ) d (√ )
x −2+8 =2 x −2+8 x −2+8
3 3 5 3 5
dx dx

45. Example
(√ )2
x − 2 + 8 . Find f′ (x).
3 5
Let f(x) =
Solu on
d (√ 5 )2 (√ ) d (√ )
x −2+8 =2 x −2+8 x −2+8
3 3 5 3 5
dx dx
(√ ) d√
x −2+8 x −2
3 5 3 5
=2
dx

46. Example
(√ )2
x − 2 + 8 . Find f′ (x).
3 5
Let f(x) =
Solu on
d (√ 5 )2 (√ ) d (√ )
x −2+8 =2 x −2+8 x −2+8
3 3 5 3 5
dx dx
(√ ) d√
x −2+8 x −2
3 5 3 5
=2
dx
(√ ) d
x − 2 + 8 1 (x5 − 2)−2/3 (x5 − 2)
3 5
=2 3
dx

47. Example
(√ )2
x − 2 + 8 . Find f′ (x).
3 5
Let f(x) =
Solu on
d (√ 5 )2 (√ ) d (√ )
x −2+8 =2 x −2+8 x −2+8
3 3 5 3 5
dx dx
(√ ) d√
x −2+8 x −2
3 5 3 5
=2
dx
(√ ) d
x − 2 + 8 1 (x5 − 2)−2/3 (x5 − 2)
3 5
=2 3
(√ ) dx
x − 2 + 8 1 (x5 − 2)−2/3 (5x4 )
3 5
=2 3

48. Example
(√ )2
x − 2 + 8 . Find f′ (x).
3 5
Let f(x) =
Solu on
d (√ 5 )2 (√ ) d (√ )
x −2+8 =2 x −2+8 x −2+8
3 3 5 3 5
dx dx
(√ ) d√
x −2+8 x −2
3 5 3 5
=2
dx
(√ ) d
x − 2 + 8 1 (x5 − 2)−2/3 (x5 − 2)
3 5
=2 3
(√ ) dx
x − 2 + 8 1 (x5 − 2)−2/3 (5x4 )
3 5
=2 3
(√
10 4 3 5 )
= x x − 2 + 8 (x5 − 2)−2/3
3

49. A metaphor
Think about peeling an onion:
(√ )2
3
f(x) = x5 −2 +8
5
√
3
+8 .
2
(√ )
′
−2+8 1 5
− 2)−2/3 (5x4 )
3
f (x) = 2 x5 3 (x
Image credit: photobunny

50. Combining techniques
Example
d ( 3 )
Find (x + 1)10 sin(4x2 − 7)
dx

51. Combining techniques
Example
d ( 3 )
Find (x + 1)10 sin(4x2 − 7)
dx
Solu on
The “last” part of the func on is the product, so we apply the product rule. Each
factor’s deriva ve requires the chain rule:

52. Combining techniques
Example
d ( 3 )
Find (x + 1)10 sin(4x2 − 7)
dx
Solu on
The “last” part of the func on is the product, so we apply the product rule. Each
factor’s deriva ve requires the chain rule:
d ( 3 )
(x + 1)10 · sin(4x2 − 7)
dx ( ) ( )
d 3 d
= (x + 1) 10
· sin(4x − 7) + (x + 1) ·
2 3 10
sin(4x − 7)
2
dx dx

53. Combining techniques
Example
d ( 3 )
Find (x + 1)10 sin(4x2 − 7)
dx
Solu on
The “last” part of the func on is the product, so we apply the product rule. Each
factor’s deriva ve requires the chain rule:
d ( 3 )
(x + 1)10 · sin(4x2 − 7)
dx ( ) ( )
d 3 d
= (x + 1) 10
· sin(4x − 7) + (x + 1) ·
2 3 10
sin(4x − 7)
2
dx dx
= 10(x3 + 1)9 (3x2 ) sin(4x2 − 7) + (x3 + 1)10 · cos(4x2 − 7)(8x)

54. Related rates of change in the ocean
Ques on
The area of a circle, A = πr2 , changes as its radius
changes. If the radius changes with respect to me,
the change in area with respect to me is
dA
A. = 2πr
dr
dA dr
B. = 2πr +
dt dt
dA dr
C. = 2πr
dt dt
.
D. not enough informa on
Image credit: Jim Frazier

55. Related rates of change in the ocean
Ques on
The area of a circle, A = πr2 , changes as its radius
changes. If the radius changes with respect to me,
the change in area with respect to me is
dA
A. = 2πr
dr
dA dr
B. = 2πr +
dt dt
dA dr
C. = 2πr
dt dt
.
D. not enough informa on
Image credit: Jim Frazier

56. Summary
The deriva ve of a
composi on is the
product of deriva ves
In symbols:
(f ◦ g)′ (x) = f′ (g(x))g′ (x)
Calculus is like an onion,
and not because it makes
you cry!