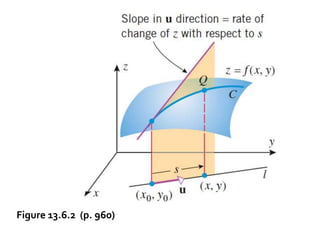
1) The document discusses partial derivatives, which involve differentiating functions of two or more variables with respect to one variable while holding the others constant. It provides examples of computing first and second partial derivatives. 2) Implicit differentiation is introduced as a way to find partial derivatives of functions defined implicitly rather than explicitly. The chain rule is also discussed. 3) Methods are presented for finding partial derivatives of functions of two or three variables, including using implicit differentiation and the chain rule. Examples are provided to illustrate these concepts.

1. PARTIAL DERIVATIVES
rahimahj@ump.edu.my
Prepared by : MISS RAHIMAH JUSOH @
AWANG

2. Objectives :
• Identify domain and range of function of
two and three variables.
• Sketch graphs and level of curves of
functions of two and three variables
• Compute first and second partial
derivatives.

3. rahimahj@ump.edu.my
Definition :
A function of two variables is a rule f that
assigns to each ordered pair (x,y)
in a set D a unique number z = f (x,y).
The set D is called the domain of the
function, and the corresponding values
of z = f (x,y) constitute the range of f .

4. Find the domains and range of the following functions
and evaluate f at the given points.
 
 
    
   
 
   
1
a) , ;
1
Eva1uate 3,2
6
: , 1 0, 1 , 3,2
2
, ,
b) , ;
2
Eva1uate 2,3 , 2,1
x y
f x y
x
f
Answer D x y x y x f
z f x y range is z z
xy
f x y
x y
f f
 


     
     


EXAMPLE 1

5. Find the domains and range of the following functions
and evaluate f at the given points.
 
   
  
   
   
 
2 2
2 2
2
c) , 25 ;
Eva1uate 2,3 , 7,4
: , 25 ,
, , 0 5
) , 3ln
Eva1uate 3,2
f x y x y
f f
Answer D x y x y
z f x y range is z z
d f x y y x
f
  
 
  
 
Continue…

6. A set of points where f is a constant is
called a level curve. A set of level
curves is called contour map.

7. Figure 13.1.4 (p. 909)

8. Figure 13.1.8 (p. 911)

9. Figure 13.1.10 (p. 912)

10. Table 13.1.2a (p. 913)

11. Table 13.1.2b (p. 913)

12. Table 13.1.2c (p. 913)

13. Table 13.1.2d (p. 913)

14. Table 13.1.2e (p. 913)

15. Table 13.1.2f (p. 913)

16.   2 2
2 2 2 2
, 9
or
3
f x y x y
z x y
  
  

17.  
2 2
, sin
2
x y
f x y
 
  
 

18. Sketch the level curves of the function
  2 2
, 9
0,1,2,3
f x y x y
for k
  

EXAMPLE 2

19.   2 2
, 9f x y x y  

20. rahimahj@ump.edu.my
Limits Along Curves
For a function one variable there two one-sided limits at a point
namely
reflecting the fact that there are only two directions from which x
can approach
0x
)(limand)(lim
00
xfxf
xxxx 

0x
Function of
2 variables
Function of
3 variables
))(),((lim),(lim
0
)Calong(
00 ),(),(
tytxfyxf
ttyxyx 

))(),(),((lim),,(lim
0
)Calong(
000 ),,(),,(
tztytxfzyxf
ttzyxzyx 


21. EXAMPLE 3
Find the limit of along22
),(
yx
xy
yxf


axis-the)( xa
axis-the)( yb
xyc linethe)(
xyd linethe)(
2
parabolathe)( xye 

22. The process of differentiating a function of
several variables with respect to one of its
variables while keeping the other variable(s)
fixed is called partial differentiation, and the
resulting derivative is a partial derivative of the
function.

23. The derivative of a function of a single variable
f is defined to be the limit of difference
quotient, namely,
Partial derivatives with respect to x or y are
defined similarly.
 
   
0
lim
x
f x x f x
f x
x 
  
 


24. If , then the partial derivatives of f with
respect to x and y are the functions and ,
respectively, defined by
and
provided the limits
exists.
 ,z f x y
xf yf
 
   
0
, ,
, limx
x
f x x y f x y
f x y
x 
  


 
   
0
, ,
, limy
y
f x y y f x y
f x y
y 
  



25. rahimahj@ump.edu.my
We can interpret partial derivatives as rates of change.
If , then represents the rate of
change of z with respect to x when y is fixed. Similarly,
is the rate of change of z with respect to y when x is
fixed.
),( yxfz  xz  /
yz  /

26. If find and
Solution :
rahimahj@ump.edu.my
,24),( 22
yxyxf  )1,1(xf ).1,1(yf
xyxfx 2),( 
2)1,1( xf
yyxfy 4),( 
4)1,1( yf
EXAMPLE 4

27. rahimahj@ump.edu.my
If calculate and .,sin),( 







yx
x
yxf
x
f


y
f


Implicit Differentiation (i)
then,variableoneoffunctionaasfunction
abledifferentiadefinesimplicitly0)If:Theorem
xy
F(x,y 
),(
),(
yxF
yxF
dx
dy
y
x

EXAMPLE 5

28. rahimahj@ump.edu.my
1543
bydefinedimplicitlyisoffunctionaasif,Find
35
 x-xy-y
xy
dx
dy
35
512
35
)512(
),(
),(
Thus
1543),(so
,1543haveWe
4
2
4
2
35
35









y
x
y
x
yxF
yxF
dx
dy
x-xy-yyxF
x-xy-y
y
x
Solution :
EXAMPLE 6

29. rahimahj@ump.edu.my
Find and if z is defined implicitly as a function of
x and y by the equation
x
z


y
z


054)(
16)(
3222
333


yzzxyzxb
xyzzyxa
Implicit Differentiation (ii)
If z = F (x, y, z) then and
z
x
F
F
x
z



z
y
F
F
y
z



EXAMPLE 7

30. rahimahj@ump.edu.my
yx
f
y
f
x
ff yyx











2
)(
x
2
2
)(
x
f
x
f
x
f
x
f xxx











xy
f
x
f
y
ff xxy











2
)(
y
2
2
)(
y y
f
y
f
y
ff yyy












31. yxxyx
y
f
y
f
xxyxyx
x
f
x
f
xxyyxxy
y
f
y
f
yxyyxxy
x
f
x
f
f
xyxyxyx
y
fyxxyyxyx
x
f
f
yxyxyxfffff
yyy
yyx
xxy
xxx
yx
yyyxxyxx
2422
32422
3233
2333
42243233432
432
,
6)3()(
46)3()(
46)42()(
122)42()(
areofderivativesecondThe
3)(,42)(
areofderivativefirstThe
),(if,,Find



































EXAMPLE 8

32. rahimahj@ump.edu.my
2323
2),( yyxxyxf Find the second partial derivatives of
xy
yyyxxyxx eyxyxfffff )(),(givenifFind ,,, 
EXAMPLE 9
EXAMPLE 10

33. rahimahj@ump.edu.my
thenexist,and,ofsderivative
partialwith)(and)(),(If:Theorem
hgf
x,yhvx,yguu,vfz 
,
,
y
v
v
z
y
u
u
z
y
z
x
v
v
z
x
u
u
z
x
z
























variablestwooffunctionfordiagramthreeThe

34. rahimahj@ump.edu.my
yvxyu
yxvyu
x
v
v
z
x
u
u
z
x
z
x
y
v
yx
x
v
xy
y
u
y
x
u
yxvxyu
v
v
z
u
u
z
vuz
yzxz
yxvxyuv
sin43
)sin2(2)(3
obtainweHence
cosy,sin2,2,
,sinandfromSimilarly
2and3
obtainwe,From
.andrulechainaUse
sin,and,uzSuppose
22
22
22
22
2
23
2233




































Solution :
EXAMPLE 11

35. rahimahj@ump.edu.my
yxyx
yxyxxyxy
yvxxyu
y
z
yxyx
yxyxyxy
yvxyu
x
z
yxvxyu
yvxxyu
yxvxyu
y
v
v
z
y
u
u
z
y
z
2sin6
cos)sin(2)(6
cos26
sin43
sin)sin(4)(3
sin43
obtainwe,sinandngSubstituti
cos26
)cos(2)2(3
.continue..
453
2222
22
2362
2222
22
22
22
22


























36. rahimahj@ump.edu.my
If where and ,
find when t = 0 .
,3 42
xyyxz  tx 2sin ty cos
dt
dz
Solution :
The Chain Rule gives
we calculate the derivatives, since we get
dt
dy
y
z
dt
dx
x
z
dt
dz






4
32 yxy
x
z


 32
12xyx
y
z



,3 42
xyyxz 
EXAMPLE 12

37. Then from and , we get
So,
Therefore
rahimahj@ump.edu.my
t
dt
dx
2cos2
tx 2sin ty cos
t
dt
dy
sin
)sin)(12()2cos2)(32( 324
txyxtyxy
dt
dy
y
z
dt
dx
x
z
dt
dz







)sin)(cos2sin122(sin)2cos2)(cos3cos2sin2( 324
tttttttt 
6)0)(00()2)(30(
0



tt
z

38. rahimahj@ump.edu.my
rules.theseformulatehelptodconstructe
becandiagramstreeand,variablesofnumberany
offunctionscompositetoappliedbecanruleChain
322
and,12,43with3
iffindtorulechaintheUse
tztytxyzxw
dtdw

Solution :
w
x
y
z
t
t
t
dt
dz
z
w
dt
dy
y
w
dt
dx
x
w
dt
dw









EXAMPLE 13

39. rahimahj@ump.edu.my
16)320(3
)12(9)(6)43(12
9612
)3(3)2(3)6(2
obtainwediagram,treetheFrom
2
232
2
2













t-tt
ttttt
ytztx
tyztx
dt
dz
z
w
dt
dy
y
w
dt
dx
x
w
dt
dw

40. rahimahj@ump.edu.my
The pressure P (in kilopascals), volume V (in liters), and
temperature T (in kelvins) of a mole of an ideal gas are related by
the equation Find the rate at which the pressure is
changing when the temperature is 300 K and increasing at a rate
0.1 K/s and the volume is 100 L and increasing at a rate of 0.2 L/s.
Solution :
If t represent the time elapsed in seconds, then at the given
instant we have
.2.0,100,1.0,300 
dt
dV
V
dt
dT
T
.31.8 TPV 
EXAMPLE 14

41. rahimahj@ump.edu.my
dt
dV
V
T
dt
dT
Vdt
dV
V
P
dt
dT
t
P
dt
dP
2
31.831.8







The chain rule gives
The pressure is decreasing at a rate of about 0.042 kPa/s.
04155.0
)2.0(
100
)300(31.8
)1.0(
100
31.8
2



42. rahimahj@ump.edu.my

43. Figure 13.6.2 (p. 960)

44. Theorem 13.6.3 (p. 961)

45. rahimahj@ump.edu.my

46. Figure 13.6.5 (p. 964)

47. Theorem 13.6.5 (p. 964)

49. rahimahj@ump.edu.my
Objective :
• Compare absolute extrema and local extrema.
• Locate critical points and determine its
classification using second partial derivatives test.

50. Definitions 13.8.1 and 13.8.2 (p. 977)

51. Figure 13.8.2 (p. 977)

52. rahimahj@ump.edu.my
function.aofvalues
minimumormaximumeitherrefer toextremumwordThe
point.saddleorpointminimumpoint,maximum-
:iespossibilitthree
has)(graphofpoint)stationary(orpointCritical

 x,yfz

53. rahimahj@ump.edu.my
R.in)(everyfor)()(such thatD,Rregion
aexiststhereif,functiontheofminimumlocalais)((ii)
R.in)(everyfor)()(such thatD,Rregion
aexiststhereif,functiontheofmaximumlocalais)((i)
Dinb)(a,thatandD,domainaindefines
variablestwooffunctionais)(Suppose
x,yx,yfa,bf
fa,bf
x,yx,yfa,bf
fa,bf
x,yfz



Definition

54. Point (a,b,f (a,b)) is a Local Maximum

55. Point (a,b,f (a,b)) is a Local Minimum

56. rahimahj@ump.edu.my
Point (a,b,f (a,b)) is a saddle point

57. A pair (a,b) such that and is
called a critical point or stationary point. To find out
whether a critical point will give f (x, y) a local maximum or
a local minimum, or will give a saddle point, we use
theorem : Second Derivative Test.
0),( bafx
0),( bafy

58. rahimahj@ump.edu.my
0)G(ifmadebecansconclusionNo(iv)
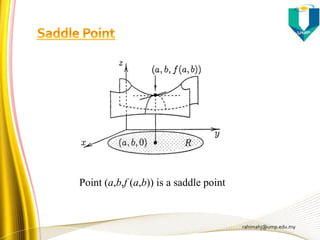
0)G(ifpointsaddleais)),(,,((iii)
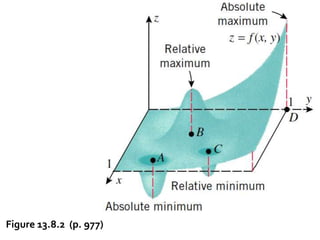
0),(and0)G(ifminimumlocalais),((ii)
0),(and0)G(ifmaximumlocalais),((i)
Then
)],([),(),(
),(),(
),(),(
)G(
LetR.inpointcriticalais
b)(a,andRregionaonsderivativepartialsecondcontinuous
hasthatvariablestwooffunctionais)(thatSuppose
2





a,b
a,bbafba
bafa,bbaf
bafa,bbaf
bafbafbaf
bafbaf
bafbaf
a,b
x,yf
xx
xx
xyyyxx
yyxy
xyxx
TestDerivativeSecond:Theorem

59. rahimahj@ump.edu.my
xyyx
yxf
yxyxyxf
yx
y
yxf
111
),()iii(
16),()ii(
3
),((i)
44
2
3



Find the critical points of the following functions and
determine whether f (x,y) at that point is a local maximum or a
local minimum, or value at a saddle point.
EXAMPLE 15

60. rahimahj@ump.edu.my
Solution :
40)2(2)G(
202
)G(andderivativesecondtheFind:3Step
1y01
002
uslysimultaneo0and0Solve:2Step
1,2
sderivativepartialfirsttheFind:1Step
3
),()i(
2
2
2
y
2
3
yyfffx,y
yfff
x,y
y
xx-
ff
yfxf
yx
y
yxf
xyyyxx
yyxyxx
yx
x








61. rahimahj@ump.edu.my
pointmaximumais)
3
2
(0,-1,,Therefore
3
2
10
3
)1(
)1,0(
02)1,0(
04)1(4G(0,-1)(0,-1)At
pointsaddleais)
3
2
(0,1,-Therefore,
3
2
10
3
1
)1,0(
04)1(4G(0,1)(0,1)At
(0,-1)and(0,1)pointTest the:4Step
3







f
f
-
f
-
xx

62. rahimahj@ump.edu.my
.onvalueextremum
theisfunctionaforextremumAbsolute
region.givenonly
on)(ofvalueextremumthefindto
usefulmoreisItns.applicatiopracticalmostfor
enoughnotisextremumlocalthefindingClearly
regiongivenany
x,yf
Definition

63. rahimahj@ump.edu.my
region.in theminimumabsolutetheisminimumlocalthe
thenregion,in thepointsaddlenoandmaximumlocal
noisthereandminimumlocalaonlyassumes)(If(ii)
region.in themaximumabsolutetheismaximumlocalthe
thenregion,in thepointsaddlenoandminimumlocal
noisthereandmaximumlocalaonlyassumes)(If(i)
R.regionaincontinuousis)(Suppose
x,yf
x,yf
x,yf
Theorem

64. rahimahj@ump.edu.my
 .0,0:),(regionin the
6),(ofextremumabsolutetheFind 33


yxyxR
xyyxyxf
Solution :
(2,2)point
criticaltheonly testweR,regiontheoutsideis(0,0)Since(2,2).and
(0,0)pointscriticalobtainweusly,simultaneoequationstheSolving
063and063
haveweThus
usly.simultaneo0),(and0),(such that)(Find
points.criticalFind:1Step
22


xyyx
yxfyxfx,y yx
EXAMPLE 16

65. rahimahj@ump.edu.my
12)2,2(thus6)(
6)2,2(thus6)(
12)22(thus6)(
(2,2)and(2,2)(2,2),Compute:2Step



xyyy
xyxy
xxxx
yyxyxx
fyx,yf
fx,yf
,fxx,yf
fff
minimum.localais
8)2)(2(622)2,2(
Therefore
012)2,2(and0108)6()12(21G(2,2)
point.criticalheclassify tandG(2,2)Compute:3Step
33
2


f
f-- xx
R.inminimumabsolutetheis
-8(2,2)minimumlocalthetherefore
R,inmaximumlocalnoisthereSince
f

66. rahimahj@ump.edu.my
“Just believe in yourself and work hard, no
matter what obstacles or hardships come in
your way. You will definitely reach your final
destination.”
66rahimahj@ump.edu.my