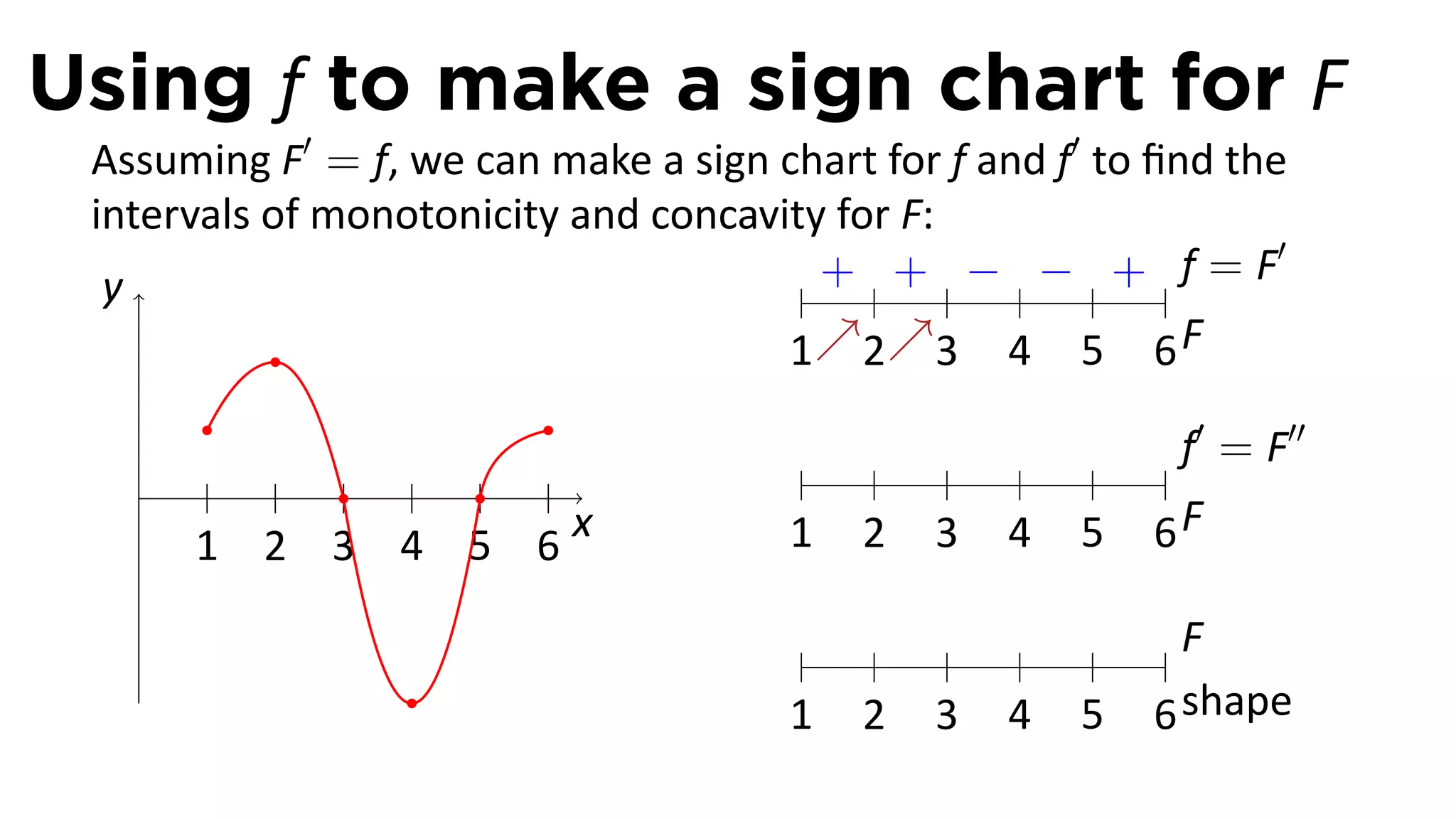
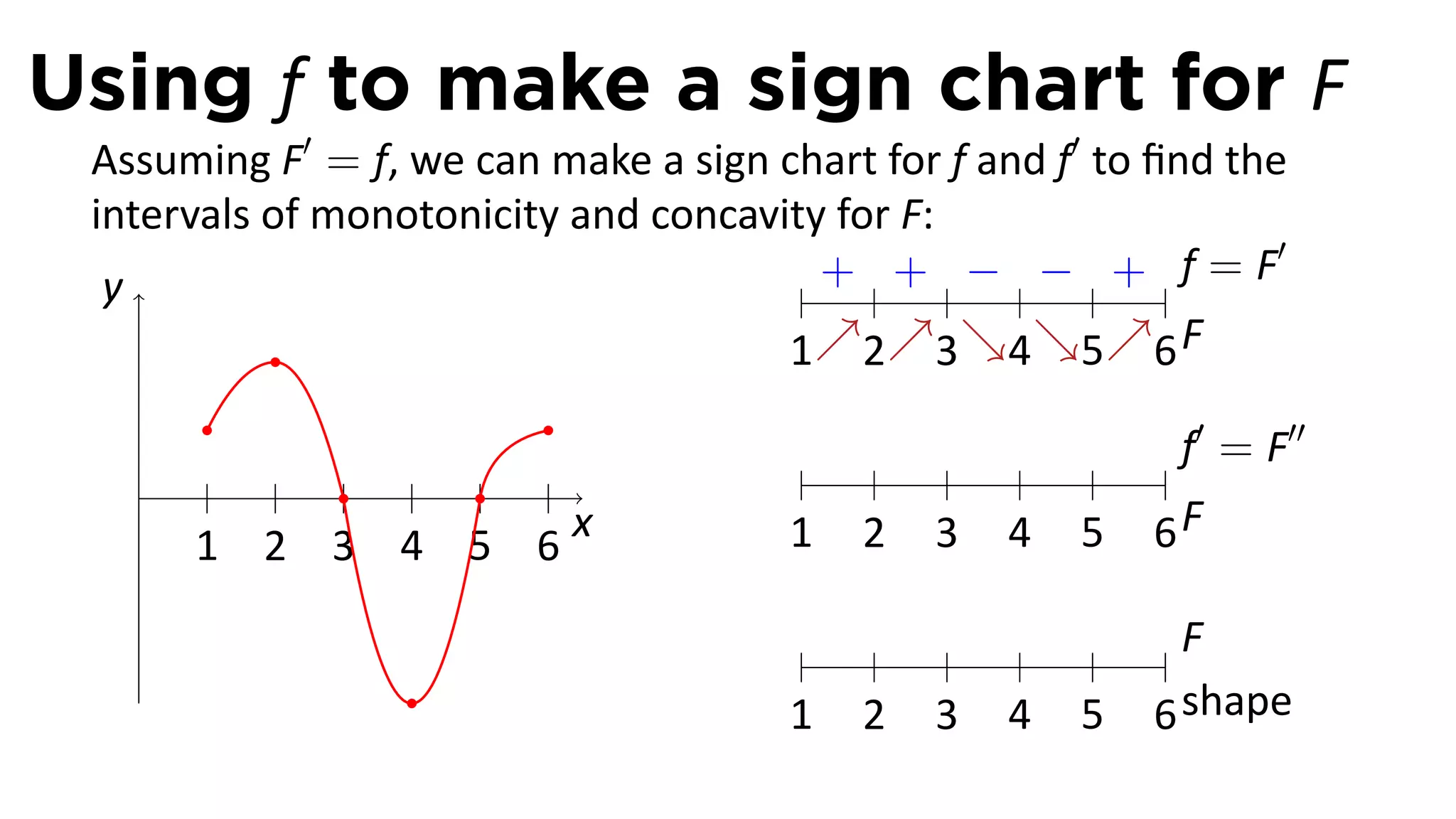
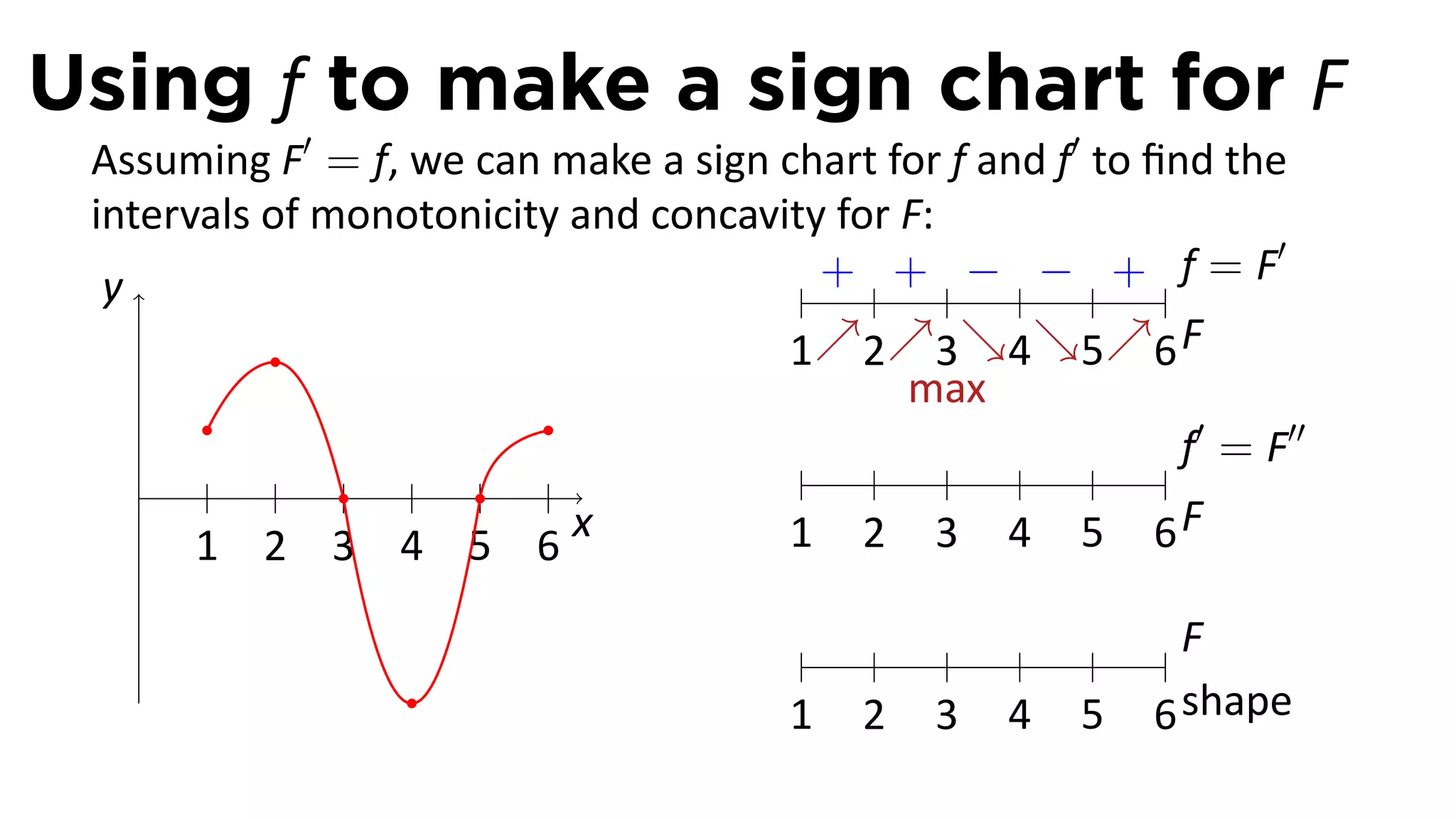
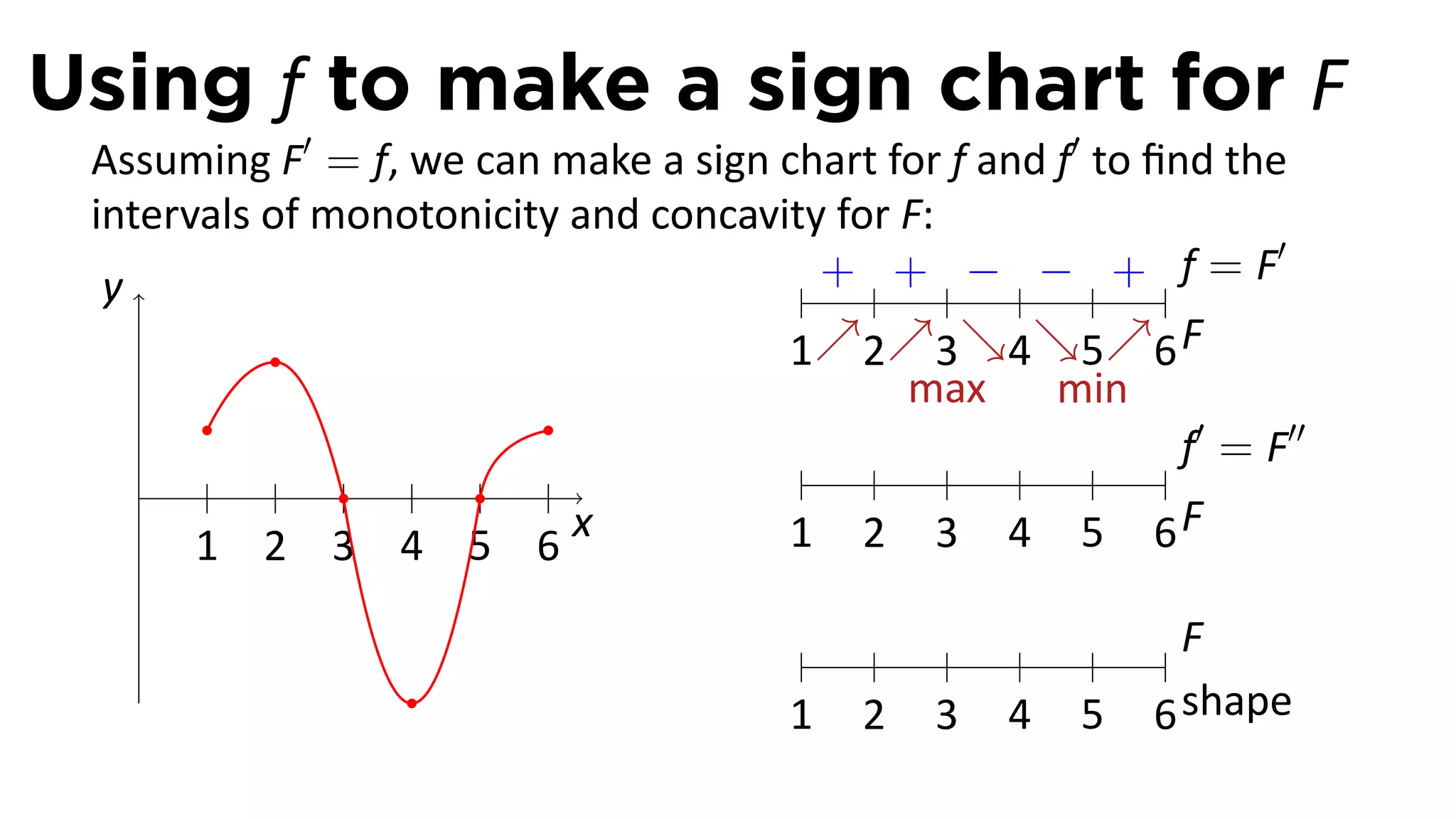
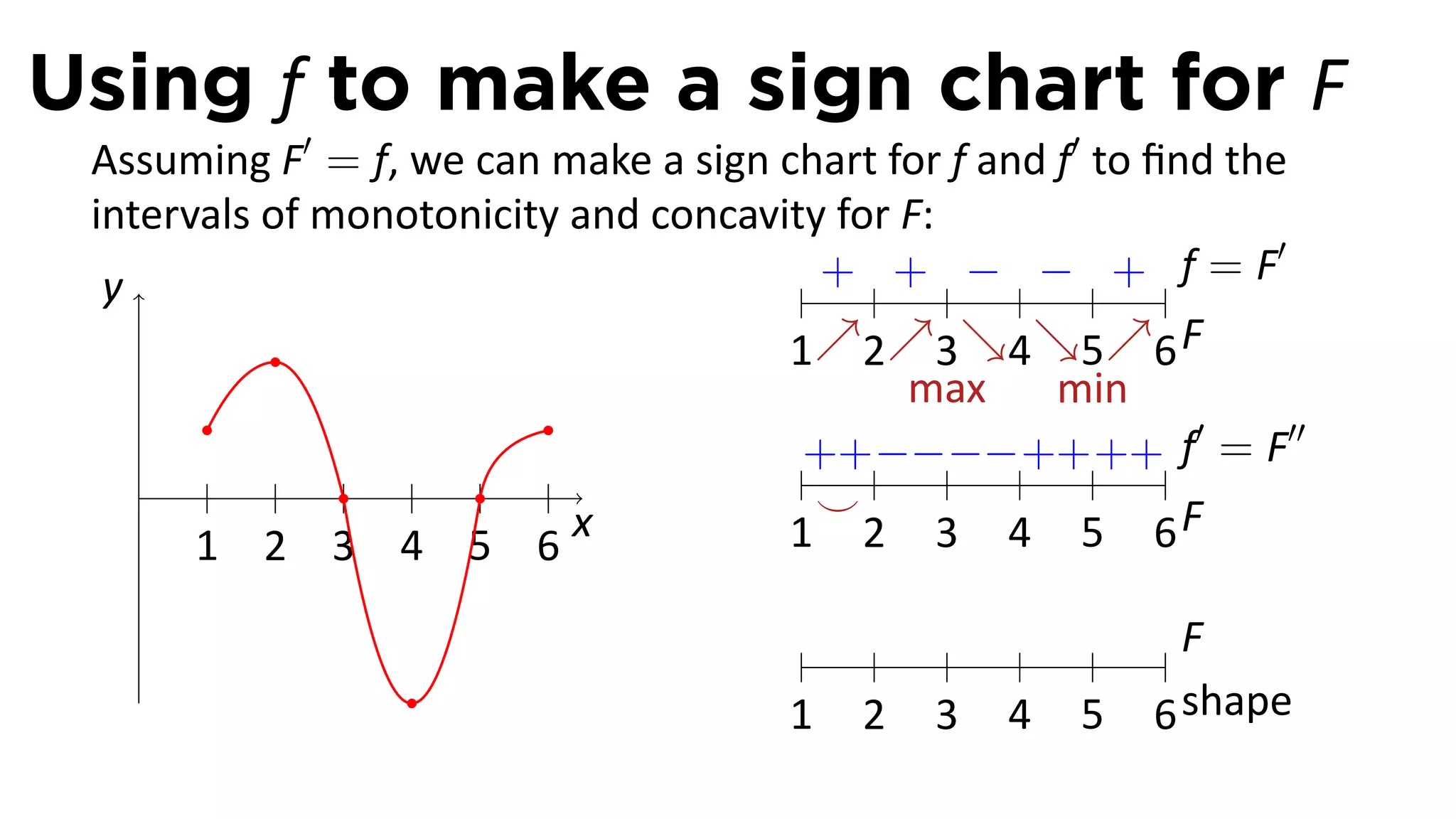
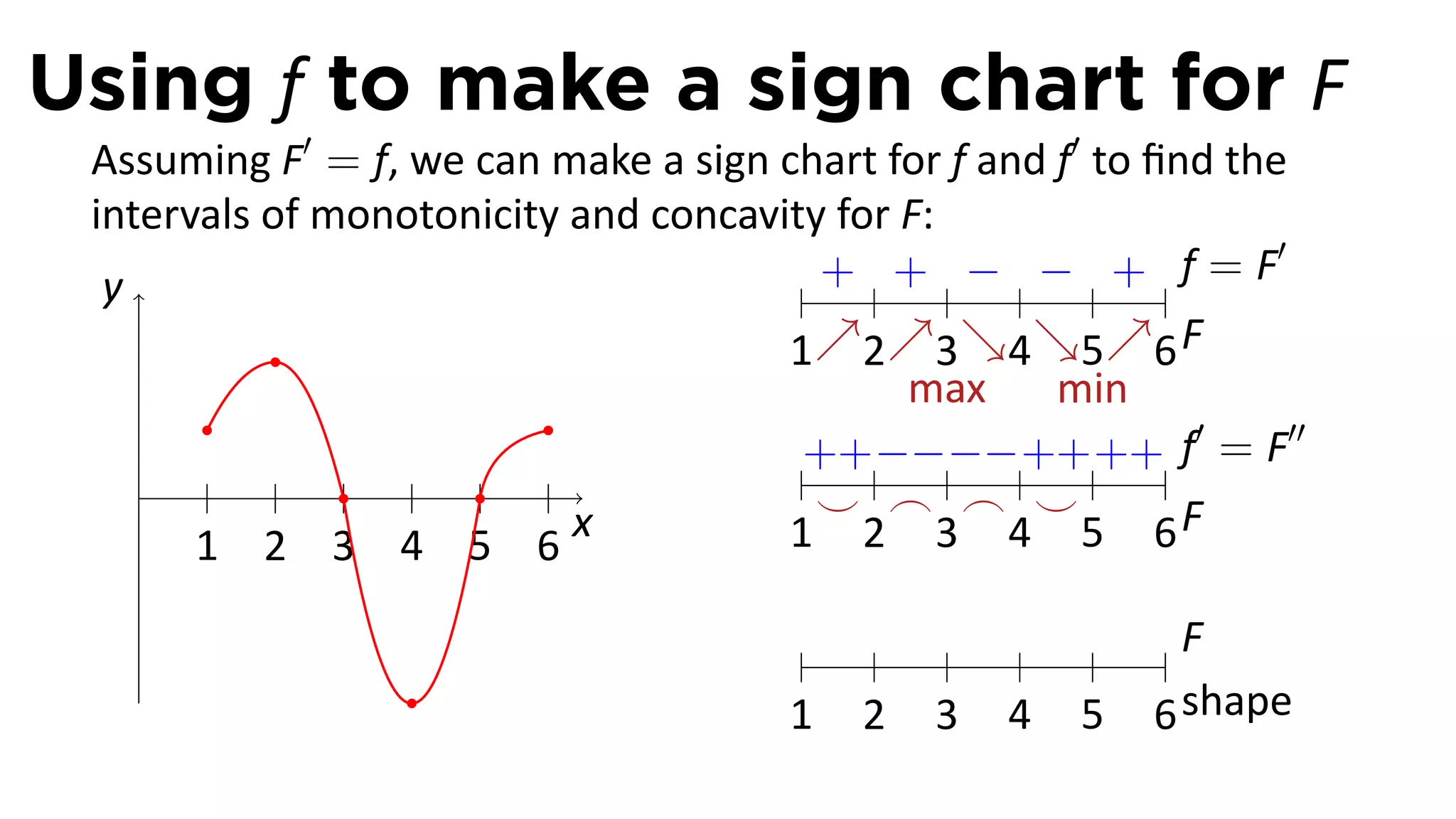
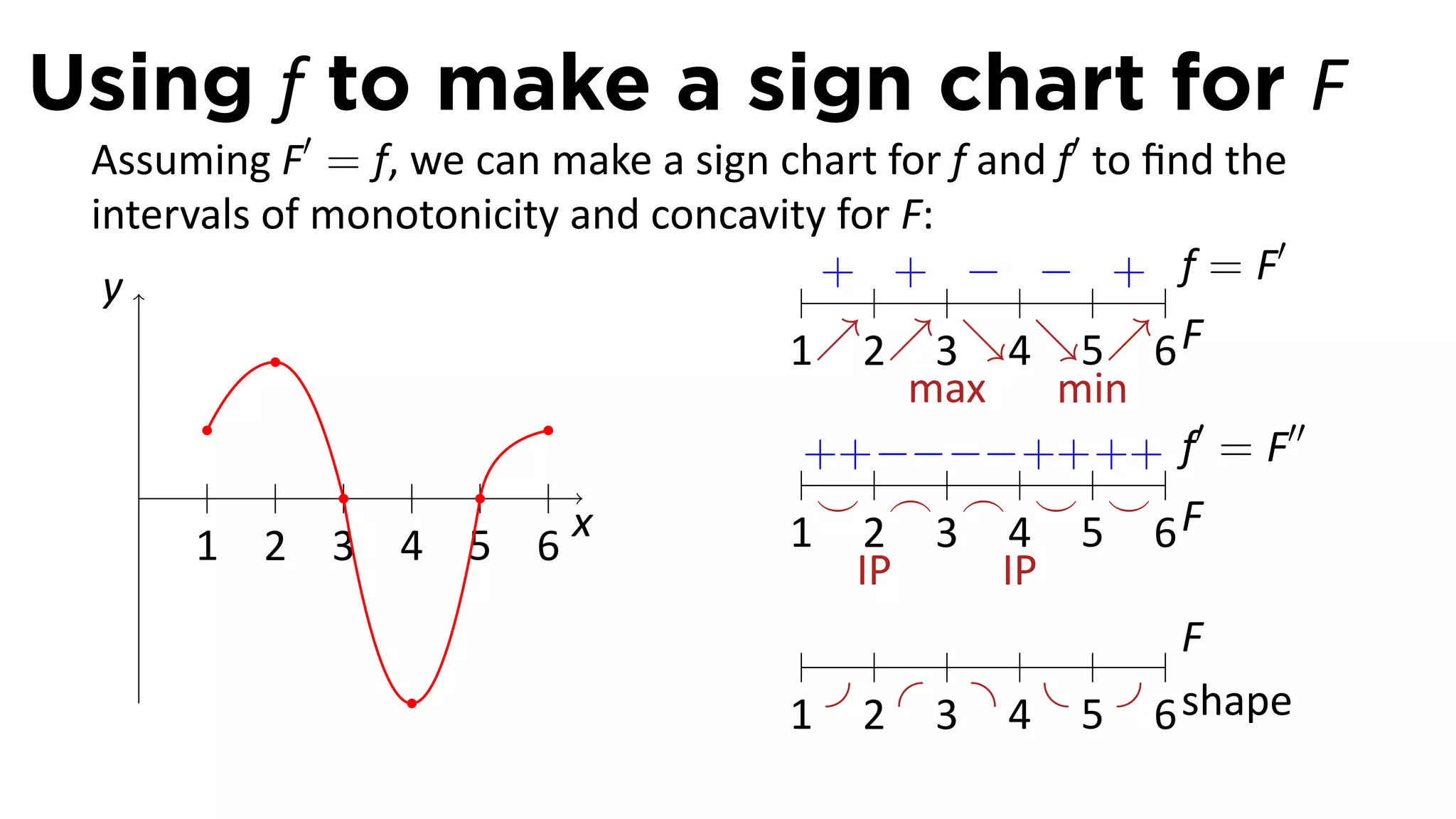
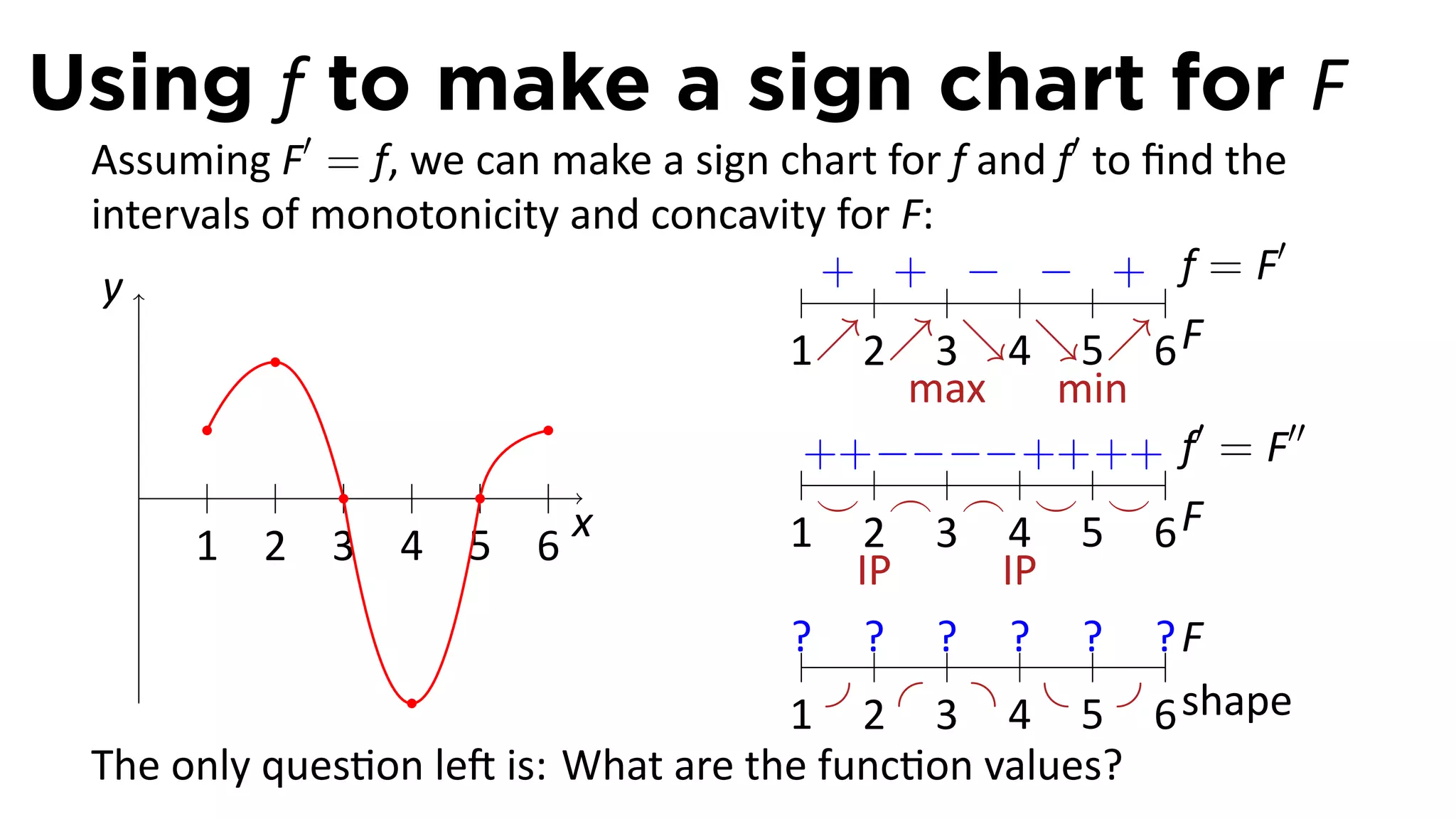
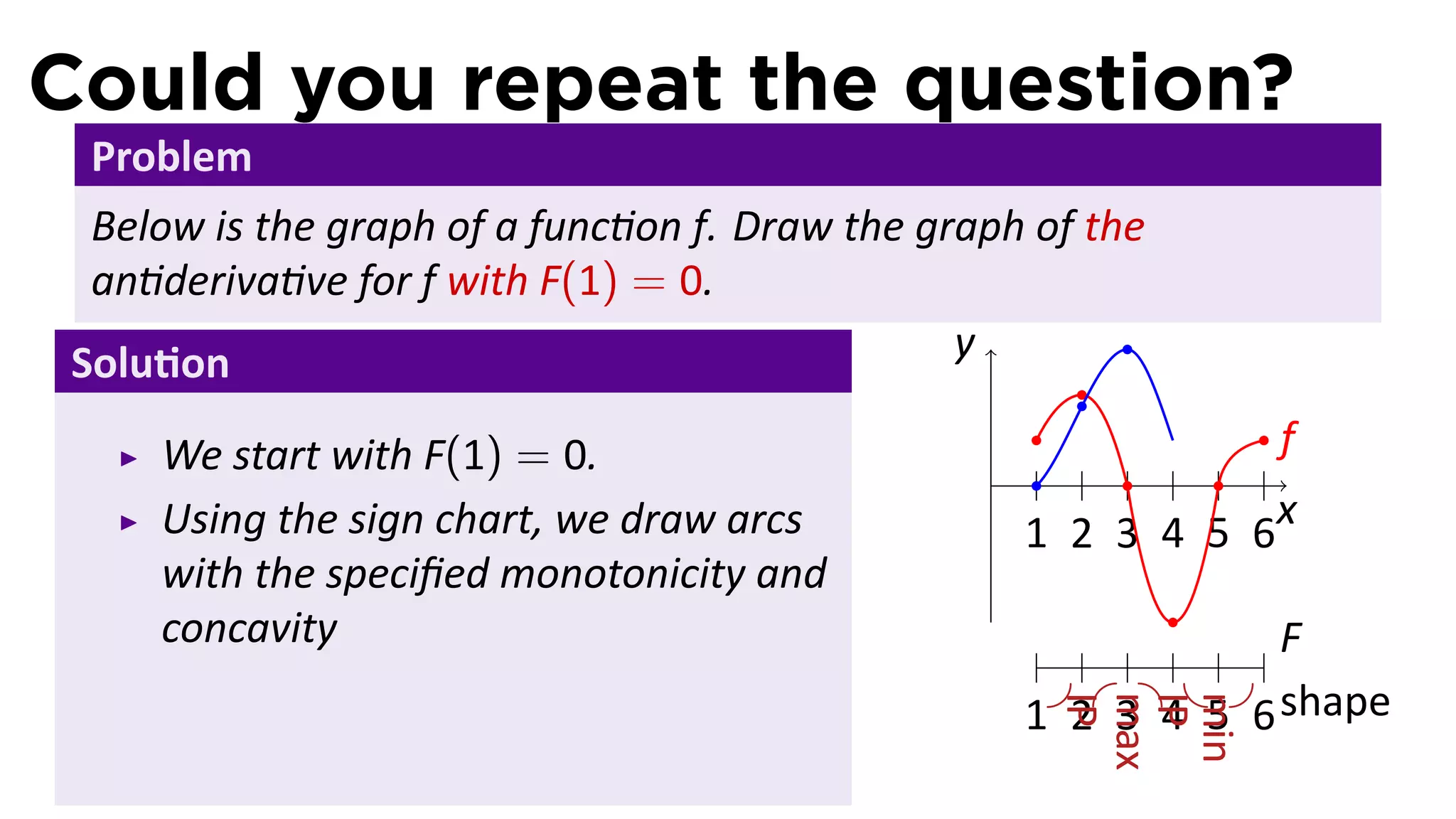
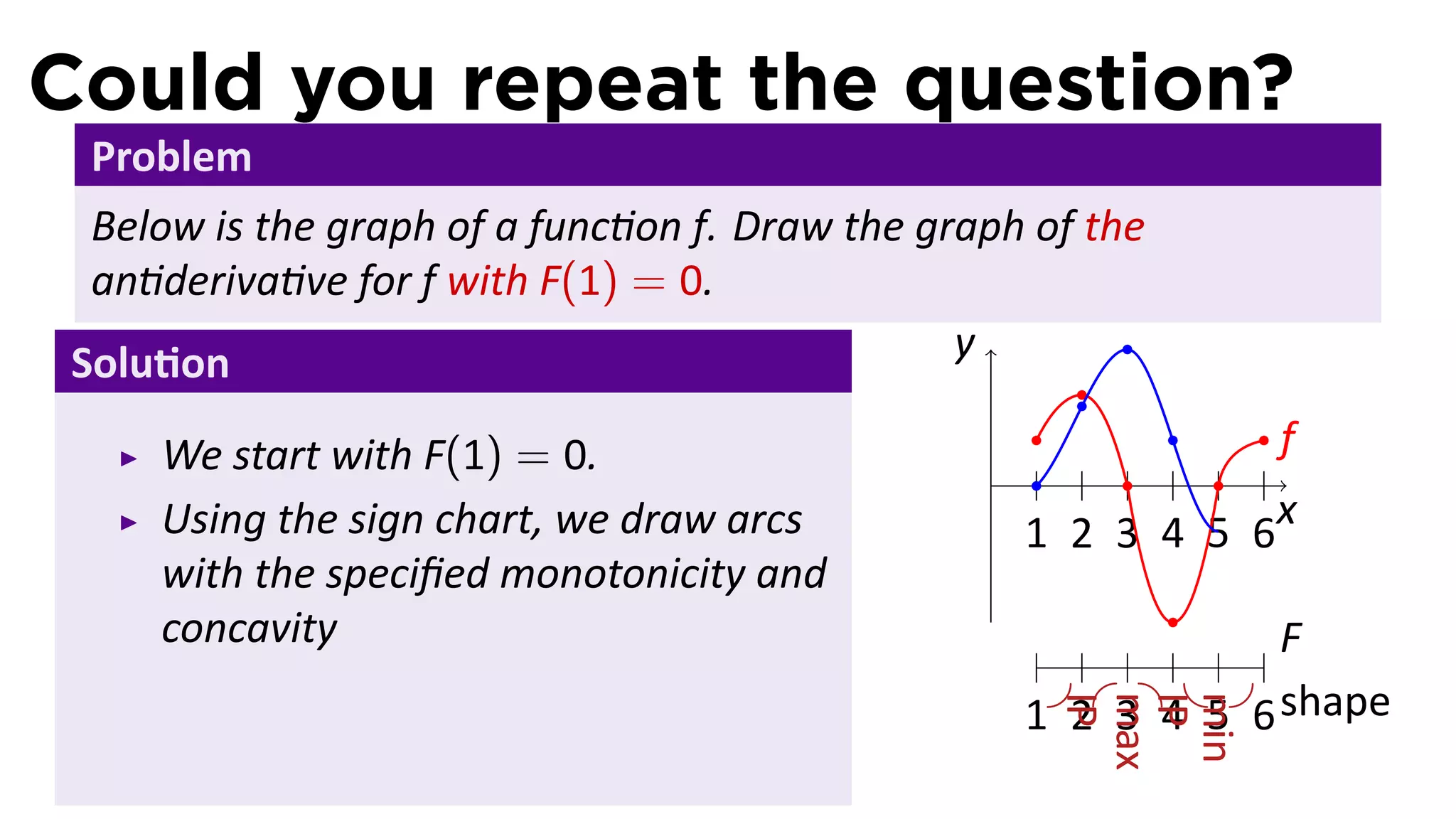
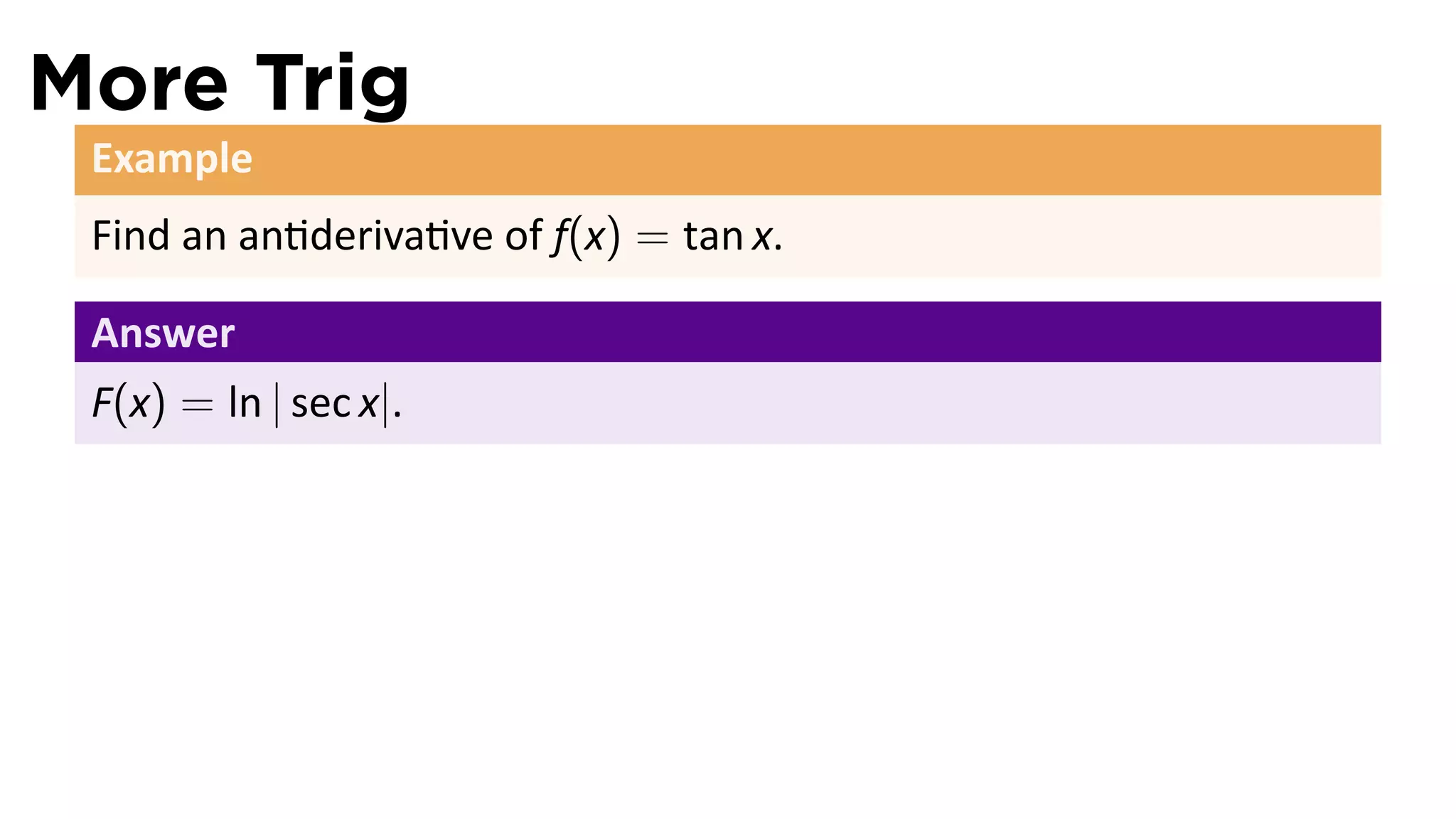The document outlines the concept of antiderivatives in calculus, focusing on various types of functions such as power, exponential, trigonometric, and logarithmic functions. It explains key theorems, provides examples of finding antiderivatives, and discusses the relationships between functions and their derivatives. Additionally, it covers the importance of the Fundamental Theorem of Calculus and includes various rules for calculating antiderivatives.