Download as PDF, PPTX
Uploaded byMatthew Leingang
PDF, PPTX5,768 views
Lesson 16: Implicit Differentiation
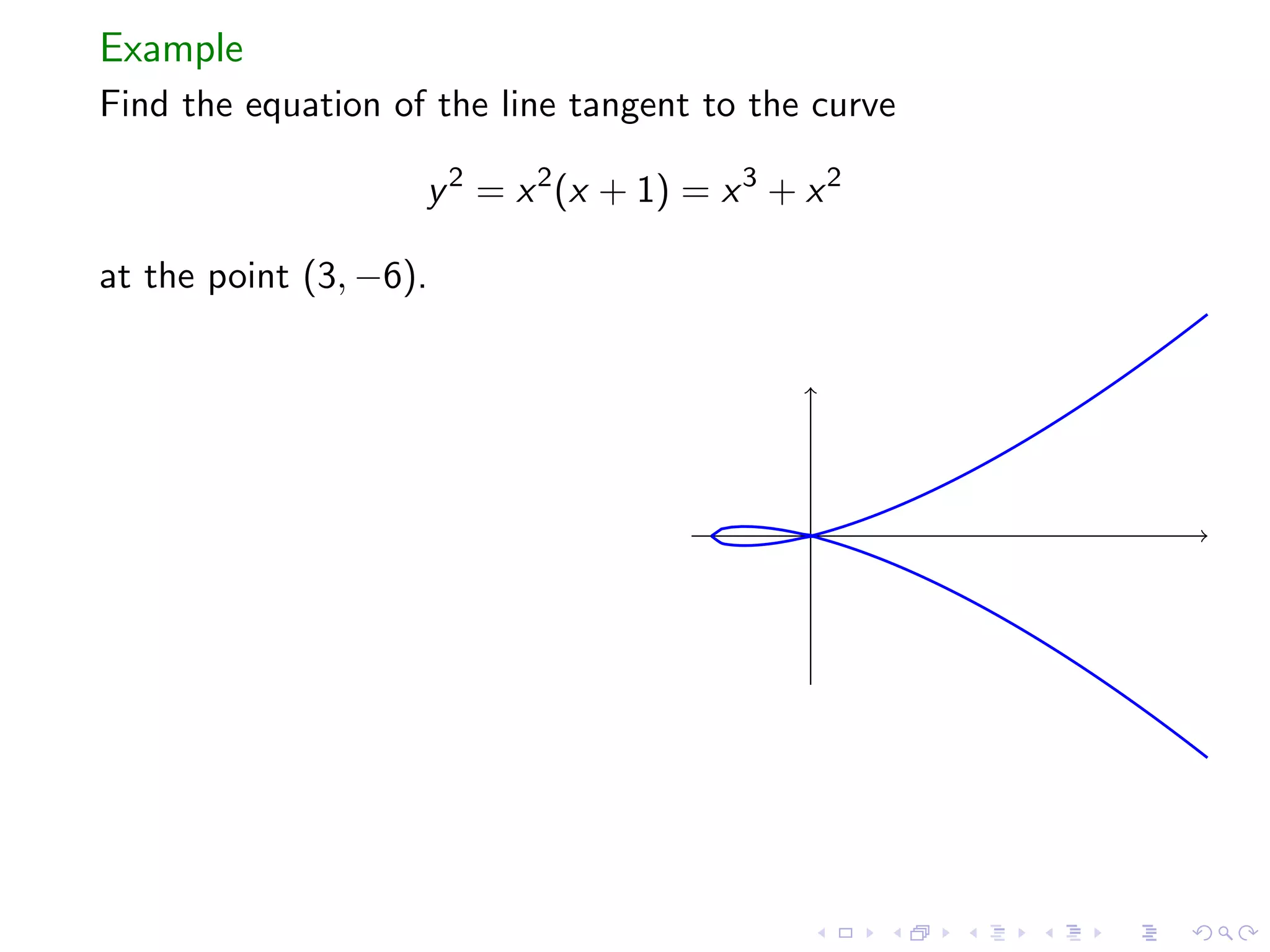
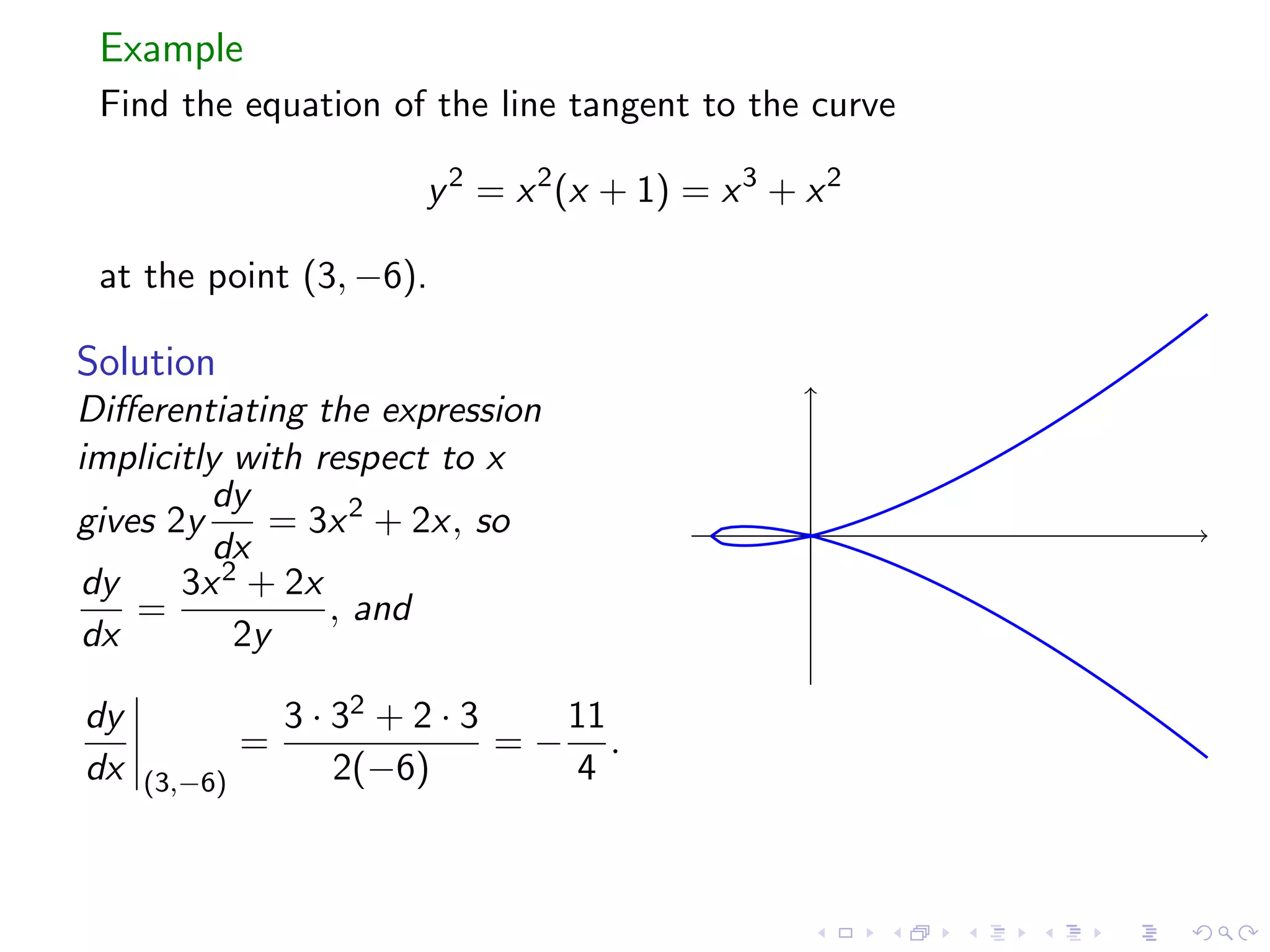
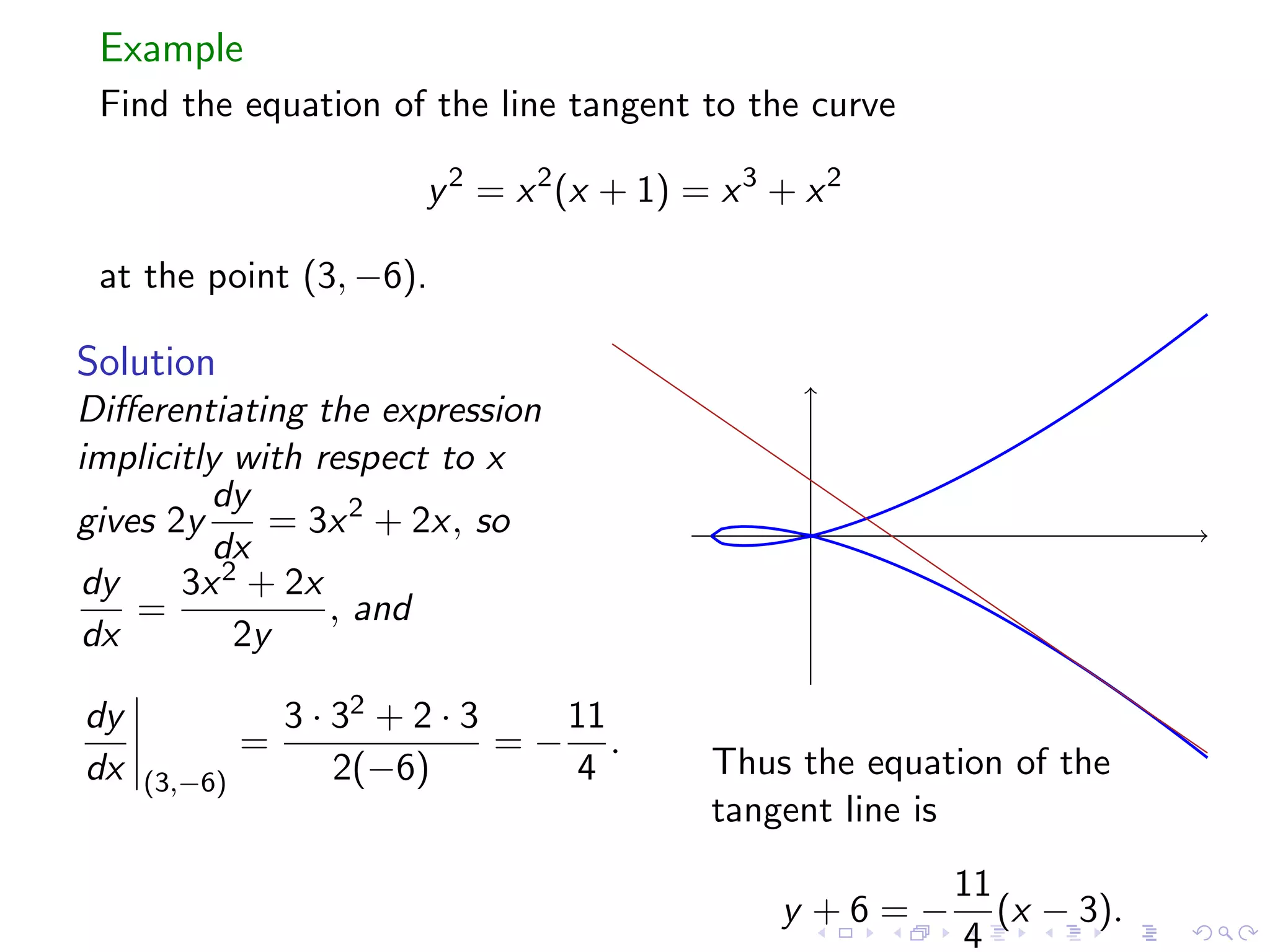
The document is a lesson on implicit differentiation and related concepts: 1) Implicit differentiation allows one to take the derivative of an implicitly defined relation between x and y, even if y is not explicitly defined as a function of x. 2) Examples are provided to demonstrate implicit differentiation, such as finding the slope of a tangent line to a curve. 3) The van der Waals equation is introduced to describe non-ideal gas properties, and implicit differentiation is used to find the isothermal compressibility of a van der Waals gas.
More Related Content
What's hot
Viewers also liked
Similar to Lesson 16: Implicit Differentiation
![Week 7 [compatibility mode]](https://cdn.slidesharecdn.com/ss_thumbnails/week7compatibilitymode-130213163717-phpapp02-thumbnail.jpg?width=640&height=640&fit=bounds)
![Week 6 [compatibility mode]](https://cdn.slidesharecdn.com/ss_thumbnails/week6compatibilitymode-130213163919-phpapp02-thumbnail.jpg?width=640&height=640&fit=bounds)
More from Matthew Leingang
Recently uploaded
![Where to Buy LinkedIn Accounts_ [12 Best Sites] (2).pdf](https://cdn.slidesharecdn.com/ss_thumbnails/wheretobuylinkedinaccounts12bestsites2-251124191348-c246988b-thumbnail.jpg?width=640&height=640&fit=bounds)
In this document
Powered by AI
Introduction to implicit differentiation, tangent lines, and derivatives of inverse functions.
Application of the van der Waals equation in gases, isothermic compressibility discussed.
Introduction to the Inverse Function Theorem and its application to derivatives.
Finding derivatives for arcsin, arccos, arctan, arcsec, and their applications.