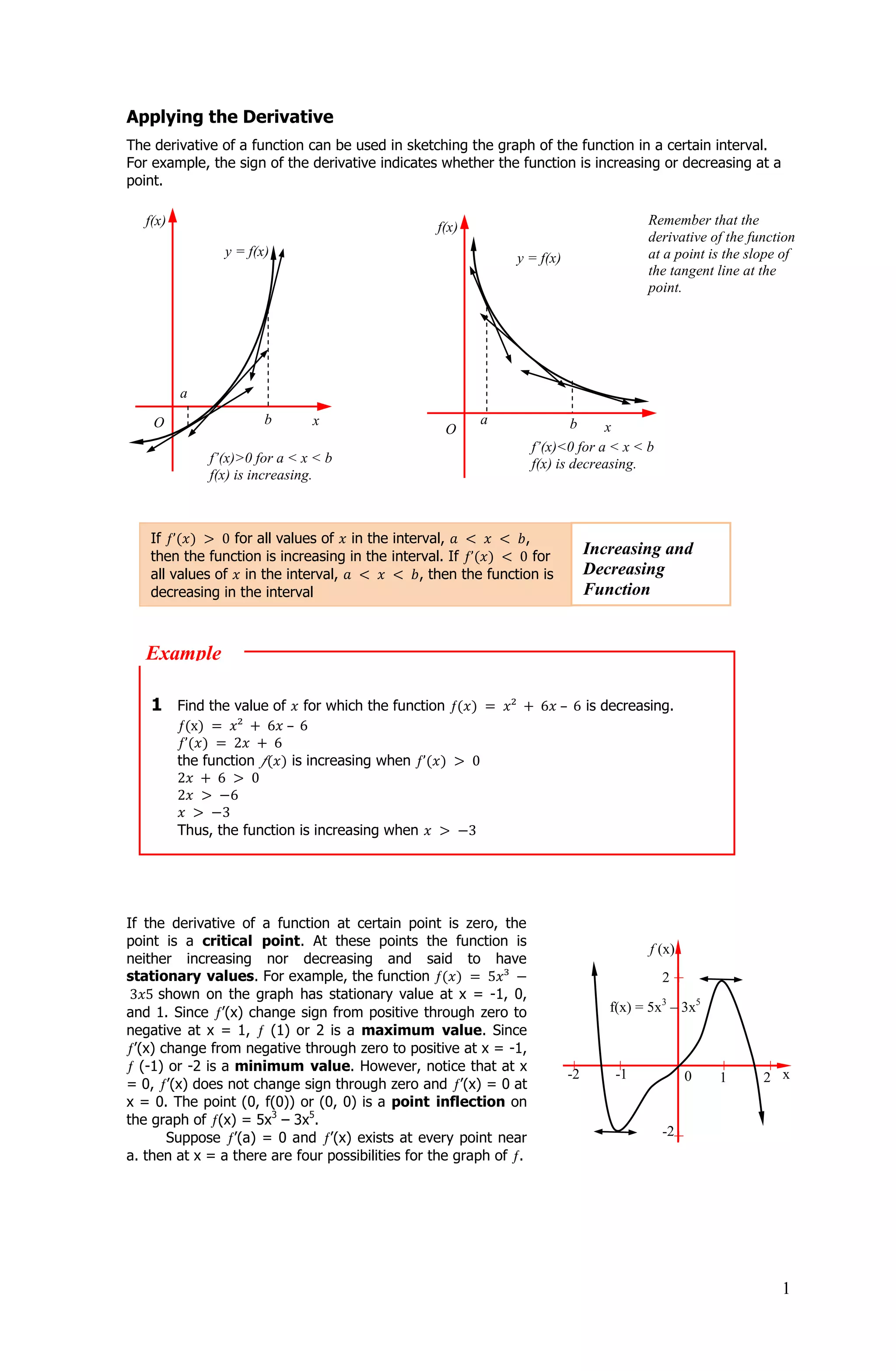
The document discusses using the derivative to determine whether a function is increasing or decreasing over an interval. It provides examples of using the sign of the derivative to determine if a function is increasing or decreasing. It also discusses using the second derivative test to determine if a stationary point is a relative maximum or minimum. Specifically: - The sign of the derivative indicates whether the function is increasing or decreasing over an interval. Positive derivative means increasing, negative means decreasing. 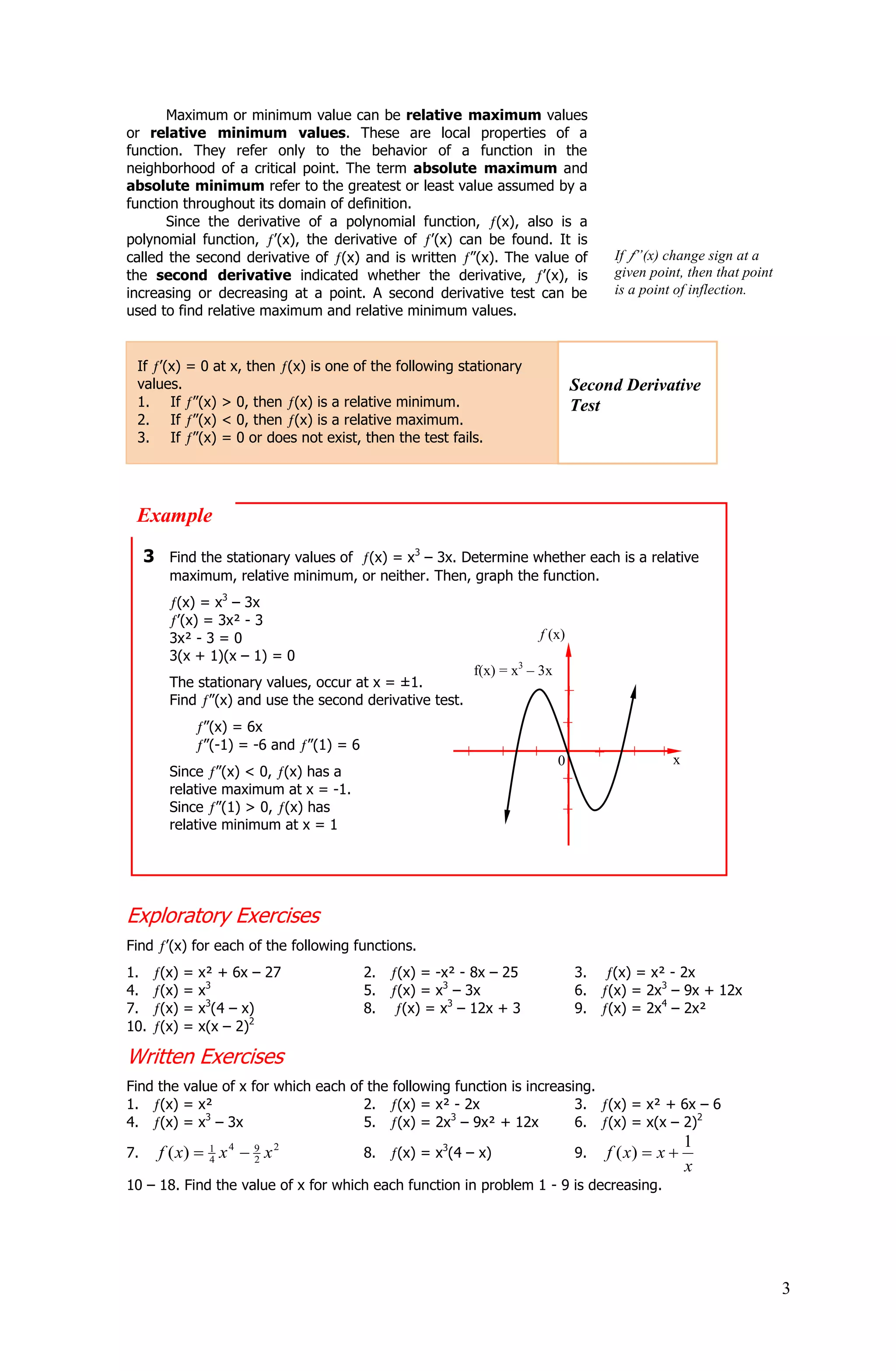- Stationary points where the derivative is zero require the second derivative test to determine if it is a relative maximum or minimum. Positive second derivative means a relative minimum, negative means a maximum. - Examples demonstrate finding stationary points, using the first and second derivative

1. Applying the Derivative
The derivative of a function can be used in sketching the graph of the function in a certain interval.
For example, the sign of the derivative indicates whether the function is increasing or decreasing at a
point.
f(x) f(x) Remember that the
derivative of the function
y = f(x) y = f(x) at a point is the slope of
the tangent line at the
point.
a
O b x a b
O x
f’(x)<0 for a < x < b
f’(x)>0 for a < x < b f(x) is decreasing.
f(x) is increasing.
If for all values of in the interval, ,
then the function is increasing in the interval. If for Increasing and
all values of in the interval, , then the function is Decreasing
decreasing in the interval Function
Example
1 Find the value of for which the function – is decreasing.
–
the function is increasing when
Thus, the function is increasing when
If the derivative of a function at certain point is zero, the
point is a critical point. At these points the function is
f (x)
neither increasing nor decreasing and said to have
stationary values. For example, the function 2+
shown on the graph has stationary value at x = -1, 0,
and 1. Since ’(x) change sign from positive through zero to f(x) = 5x3 – 3x5
negative at x = 1, (1) or 2 is a maximum value. Since
’(x) change from negative through zero to positive at x = -1,
(-1) or -2 is a minimum value. However, notice that at x + + + +
-2 -1 0 1 2 x
= 0, ’(x) does not change sign through zero and ’(x) = 0 at
x = 0. The point (0, f(0)) or (0, 0) is a point inflection on
the graph of (x) = 5x3 – 3x5.
Suppose ’(a) = 0 and ’(x) exists at every point near -2+
a. then at x = a there are four possibilities for the graph of .
1

2. f (x) f (x)
f (a)
+
- + -
f (a)
0 a x 0 a x
f (a) is a minimum f (a) is a
value maximum value
Points of inflection occur
f (x) f (x)
whenever a function has
change in concavity. That is,
+ - it goes from concave up to
f (a) f (a) concave down or vice versa.
+ -
0 a x 0 a x
Point (a, f (a)) is a point of inflection
Example
2 Find the stationary values of (x) = x3(4x – x). Determine whether each is a
maximum, minimum, or a point of inflection.
(x) = x3(4x – x)
= 4x3 – x4
’(x) = 12x² - 4x3
= 4x²(3 – x)
To find the stationary values, let ’(x) = 0
4x²(3 – x) = 0
X = 0 or x = 3
Thus, f has stationary value at x = 0 and x = 3.
Determine values of ’(x) near 0.
’(- 0.1) = 4(-0.4)²(3 + 0.1) or 0.124 (x) is increasing
’(0.1) = 4(0.4)²(3 - 0.1) or 0.116 (x) is increasing
Since f’(x) does not change sign through zero at x = 0,
the point (0, f(0)) or (0, 0) is a point of inflection.
Determine values of x near 3
’(2.9) = 4(2.9)²(3 – 2.9) or 3.364 (x) is increasing
’(3.1) = 4(3.1)²(3 – 3.1) or -3.844 is decreasing
Since ’(x) change sing from positive though zero to negative at x =3, (3) is a
maximum value,
2

3. Maximum or minimum value can be relative maximum values
or relative minimum values. These are local properties of a
function. They refer only to the behavior of a function in the
neighborhood of a critical point. The term absolute maximum and
absolute minimum refer to the greatest or least value assumed by a
function throughout its domain of definition.
Since the derivative of a polynomial function, (x), also is a
polynomial function, ’(x), the derivative of ’(x) can be found. It is
called the second derivative of (x) and is written ”(x). The value of If ”(x) change sign at a
the second derivative indicated whether the derivative, ’(x), is given point, then that point
increasing or decreasing at a point. A second derivative test can be is a point of inflection.
used to find relative maximum and relative minimum values.
If ’(x) = 0 at x, then (x) is one of the following stationary
values. Second Derivative
1. If ”(x) > 0, then (x) is a relative minimum. Test
2. If ”(x) < 0, then (x) is a relative maximum.
3. If ”(x) = 0 or does not exist, then the test fails.
Example
3 Find the stationary values of (x) = x3 – 3x. Determine whether each is a relative
maximum, relative minimum, or neither. Then, graph the function.
(x) = x3 – 3x
’(x) = 3x² - 3
3x² - 3 = 0 f (x)
3(x + 1)(x – 1) = 0
f(x) = x3 – 3x
The stationary values, occur at x = ±1.
Find ”(x) and use the second derivative test.
+
”(x) = 6x +
”(-1) = -6 and ”(1) = 6 + + + 0 + +x
+
Since ”(x) < 0, (x) has a
+
relative maximum at x = -1.
Since ”(1) > 0, (x) has +
relative minimum at x = 1
Exploratory Exercises
Find ’(x) for each of the following functions.
1. (x) = x² + 6x – 27 2. (x) = -x² - 8x – 25 3. (x) = x² - 2x
4. (x) = x3 5. (x) = x3 – 3x 6. (x) = 2x3 – 9x + 12x
7. (x) = x3(4 – x) 8. (x) = x3 – 12x + 3 9. (x) = 2x4 – 2x²
10. (x) = x(x – 2)2
Written Exercises
Find the value of x for which each of the following function is increasing.
1. (x) = x² 2. (x) = x² - 2x 3. (x) = x² + 6x – 6
4. (x) = x3 – 3x 5. (x) = 2x3 – 9x² + 12x 6. (x) = x(x – 2)2
1
7. f ( x)  1 x 4  9 x 2
4 2
8. (x) = x3(4 – x) 9. f ( x)  x 
x
10 – 18. Find the value of x for which each function in problem 1 - 9 is decreasing.
3

4. Find the stationary values of each of the following functions. State whether each is a maximum,
minimum. Or neither. Then, graph the function.
19. (x) = x - x² 20. (x) = x3 21. (x) = 2x3 – 9x² + 12x
22. f ( x)  1 x  9 x 23. (x) = x3(4 – x) 24. (x) = 2x4 – 2x2
4 2
2 2
Differentiation techniques may be used to solve problem in which maximum or minimum solution
are necessary. Consider the following example.
Example Suppose a rectangle field along a straight river is to be
fenced. There are 300 m of fencing available. What is
the greatest area that can be enclosed?
Let the width of the field be x meters. Then, the
length is 300 – 2x meters. The area in square meters
is A = x(300 -2x) or 300x – 2x . This defines a
2
function for which (x) = 300x -2x2.
Since x ≥ 0 and 300 – 2x ≥ 0, the maximum value
must be in the interval 0 ≤ x ≤ 150
4