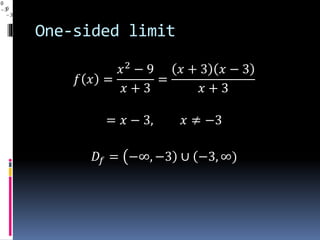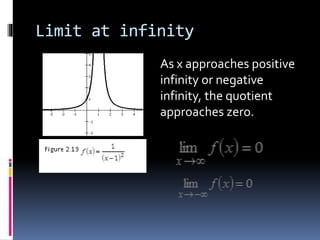
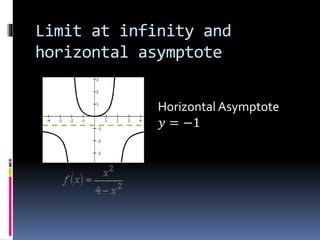
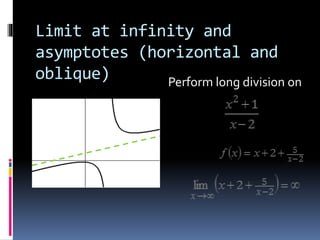
1) One-sided limits describe the value a function approaches as the input gets closer to a number from the left or right. 2) The limit of a function exists if and only if the one-sided limits are equal as the input approaches the number. 3) Limits at infinity describe the value a function approaches as the input increases without bound toward positive or negative infinity.

1. LIMIT OF FUNCTIONS
One-sided limit, limit, existence of limit, limit at infinity, infinite limit

2. One-sided limit
Given a function defined by 𝑦 = 𝑓 𝑥
lim
𝑥→𝑎+
𝑓 𝑥
Is the value y (real number) being approached by
f(x) as x gets closer and closer to a from the
right.

3. One-sided limit
Given a function defined by 𝑦 = 𝑓 𝑥
lim
𝑥→𝑎−
𝑓 𝑥
Is the value y (real number) “being approached”
by f(x) as x gets closer and closer to a from the
left.

4. One-sided limit
Consider the function defined by
a. Evaluate lim
𝑥→−3−
𝑓 𝑥
b. Evaluate lim
𝑥→−3+
𝑓 𝑥

5. One-sided limit
𝑓 𝑥 =
𝑥2
− 9
𝑥 + 3
=
𝑥 + 3 𝑥 − 3
𝑥 + 3
= 𝑥 − 3, 𝑥 ≠ −3
𝐷𝑓 = −∞, −3 ∪ −3, ∞
0
3 0
3

6. One-sided limit
 
3
92



x
x
xf
x  
3
92



x
x
xf x  
3
92



x
x
xf
-3.1 -6.1 -2.9 -5.9
-3.01 -6.01 -2.99 -5.99
-3.001 -6.001 -2.999 -5.999
-3.0001 -6.0001 -2.9999 -5.9999
Table 2.1 Some numerical computations close to -3
from the left and right

7. One-sided limit
 
3
92



x
x
xf
Theorem 2.1 Existence of Limit
The limit of a function exists if and only if the one-
sided limits of the function are equal
lim
𝑥→𝑎+
𝑓 𝑥 = lim
𝑥→𝑎−
𝑓 𝑥

8. One-sided limit
Given a function defined by
𝑓 𝑥 =
𝑥2
− 9
𝑥 + 3
lim
𝑥→−3−
𝑓 𝑥 = lim
𝑥→−3+
𝑓 𝑥
lim
𝑥→−3
𝑓 𝑥 = −6

9. One-sided limit
Functions whose limit at a does not exist.
Example 2.1
Evaluate lim
𝑥→1
𝑓 𝑥 , does it exist?

10. One-sided limit
a. Evaluate lim
𝑥→1−
𝑓 𝑥 and lim
𝑥→1+
𝑓 𝑥 .
b. Are they equal?
Conclusion: the limit does not exist

11. One-sided limit
Function whose limit does not exist at a.
Example 2.4
Evaluate lim
𝑥→3
𝑓 𝑥 where
𝑓 𝑥 =
3𝑥 + 9
𝑥2 − 9

12. One-sided limit
The limits do not point to a specific real
number. Conclusion: limit does not exist as
x approaches 3

13. Limit Theorems

14. Limit at infinity
Evaluate lim
𝑥→∞
𝑓 𝑥 and lim
𝑥→−∞
𝑓 𝑥 , where

15. Limit at infinity
As x approaches positive
infinity or negative
infinity, the quotient
approaches zero.

16. Limit at infinity
Evaluate lim
𝑥→∞
𝑓 𝑥 where
Solution

17. Limit at Infinity and
Horizontal Asymptote
Obtain the horizontal asymptote of
Solution

18. Limit at infinity and
horizontal asymptote
Horizontal Asymptote
𝑦 = −1

19. Limit at infinity and
asymptotes (horizontal and
oblique)

20. Limit at infinity and
asymptotes (horizontal and
oblique)
Examples

21. Limit at infinity and
asymptotes (horizontal and
oblique) Perform long division on

22. Limit of some trigonometric
functions
Theorems
lim
𝑥→0
sin 𝑥
𝑥
= 1 lim
𝑥→0
cos 𝑥−1
𝑥
= 0

23. Limit of trigonometric
functions

24. Limit of trigonometric
functions

25. Limit of trigonometric
functions

26. Limit of trigonometric
functions