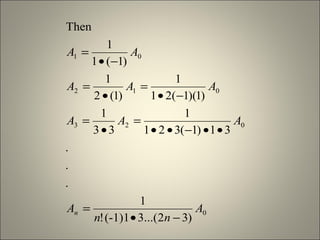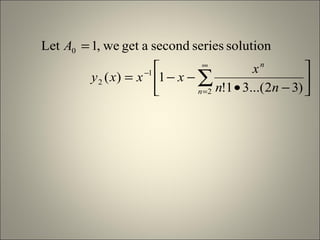The document discusses the Method of Frobenius for solving ordinary differential equations (ODEs) with singular points. It states that the solution for such an ODE is given as an infinite series involving powers of x. To determine the coefficients in the series, one substitutes the series solution into the original ODE, equates coefficients of like powers of x, and obtains the indical equation. Solving this indical equation gives the indicial solution and recurrence relations for the coefficients.

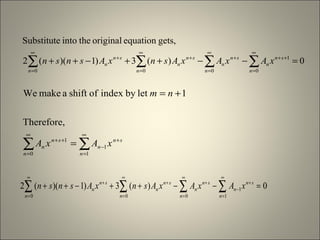
1. The Method Of Frobenius

2. Methods of Frobenius
• If x is not analytic, it is a singular point.
)()()()( '''
xfyxqyxpyxr =++
→
)(
)(
)(
)(
)(
)( '''
xr
xf
y
xr
xq
y
xr
xp
y =++
The points where r(x)=0 are called as singular points.

3. Methods of Frobenius (Cont’d)
• The solution for such an ODE is given as,
∑
∞
=
=
0m
m
m
r
xaxy
Substituting in the ODE for values of , )(),(),( '''
xyxyxy
equating the coefficient of xm
and obtaining the roots
gives the indical solution

4. .0atanalyticare)(and)(and
2
1
)(and,
2
3
)(
with
0)()(
aswrittenbecanequationThe
2
2
=
+
−==
=+′+′′
xxqxxxp
x
x
xq
x
xp
yxqyxpy
.0atpointsingularregularahas0)1(32equationThe 2
==+−′+′′ xyxyxyx
∑
∑
∑∑
∞
=
−+
∞
=
−+
∞
=
+
∞
=
+−+=′′
+=′
==
0
2
0
1
00
))(1()(
)()(
)(
n
sn
n
n
sn
n
n
sn
n
n
n
n
s
xAsnsnxy
xAsnxy
xAxAxxy

5. 0)(3)1)((2
gets,equationoriginaltheintoSubstitute
0
1
000
=−−++−++ ∑∑∑∑
∞
=
++
∞
=
+
∞
=
+
∞
=
+
n
sn
n
n
sn
n
n
sn
n
n
sn
n xAxAxAsnxAsnsn
∑∑
∞
=
+
−
∞
=
++
=
+=
1
1
0
1
Therefore,
1letbyindexofshiftamakeWe
n
sn
n
n
sn
n xAxA
nm
0)(3)1)((2
1
1
000
=−−++−++ ∑∑∑∑
∞
=
+
−
∞
=
+
∞
=
+
∞
=
+
n
sn
n
n
sn
n
n
sn
n
n
sn
n xAxAxAsnxAsnsn

6. ∑
∞
=
+
− =−−++−+++−+−
1
10 0}]1)(3)1)((2{[]13)1(2[
n
sn
nn
s
xAAsnsnsnxAsss
1or
0)1)(12(
or
013)1(2
then,0Since
22
1
1
0
−==
=+−
=−+−
≠
ss
ss
sss
A
1,]1)(3)1)((2[ 1 ≥=−++−++ − nAAsnsnsn nn

7. 1,
)32(
1
or
)32(
becomesthis,When
1
1
2
1
≥
+
=
=+
=
−
−
nA
nn
A
AAnn
s
nn
nn
0
012
01
)32...(75!
1
.
.
.
)75)(21(
1
72
1
51
1
Then
A
nn
A
AAA
AA
n
+•
=
••
=
•
=
•
=

8. 





+•
+=
=
∑
∞
=1
1
0
)32...(75!
1)(
solutionseriesgetwe,1Let
2
1
n
n
nn
x
xxy
A
1,
)32(
1
or
)32(
becomesrelationrecurrencethe,1When
1
1
≥
−
=
=−
−=
−
−
nA
nn
A
AAnn
s
nn
nn

9. 0
023
012
01
)32...(3(-1)1!
1
.
.
.
31)1(321
1
33
1
)1)(1(21
1
)1(2
1
)1(1
1
Then
A
nn
A
AAA
AAA
AA
n
−•
=
••−••
=
•
=
−•
=
•
=
−•
=

10. 





−•
−−=
=
∑
∞
=
−
2
1
2
0
)32...(31!
1)(
solutionseriessecondagetwe,1Let
n
n
nn
x
xxxy
A