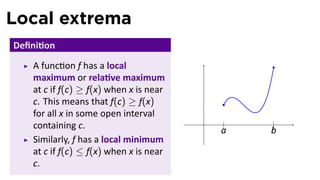
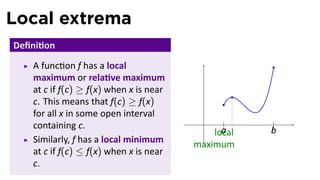
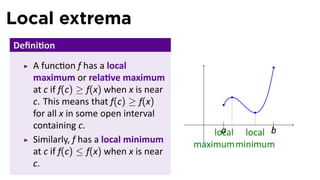
The document outlines the concepts of maximum and minimum values in calculus, focusing on the Extreme Value Theorem and Fermat's Theorem. It explains the conditions under which a function can attain absolute maximum and minimum values, emphasizing the importance of continuity and closed intervals. Examples included illustrate methods for finding these extrema for both linear and quadratic functions.















![The Extreme Value Theorem
Theorem (The Extreme Value
Theorem)
Let f be a func on which is
con nuous on the closed
interval [a, b]. Then f a ains
an absolute maximum value
f(c) and an absolute minimum
value f(d) at numbers c and d
in [a, b].](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-16-320.jpg)
![The Extreme Value Theorem
Theorem (The Extreme Value
Theorem)
Let f be a func on which is
con nuous on the closed
interval [a, b]. Then f a ains
an absolute maximum value
f(c) and an absolute minimum
value f(d) at numbers c and d .
in [a, b]. a b](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-17-320.jpg)
![The Extreme Value Theorem
Theorem (The Extreme Value
Theorem) maximum
value
Let f be a func on which is f(c)
con nuous on the closed
interval [a, b]. Then f a ains
an absolute maximum value
f(c) and an absolute minimum
value f(d) at numbers c and d .
a c
in [a, b]. b
maximum](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-18-320.jpg)
![The Extreme Value Theorem
Theorem (The Extreme Value
Theorem) maximum
value
Let f be a func on which is f(c)
con nuous on the closed
interval [a, b]. Then f a ains minimum
an absolute maximum value value
f(c) and an absolute minimum f(d)
value f(d) at numbers c and d .
a d c
in [a, b]. b
minimum maximum](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-19-320.jpg)



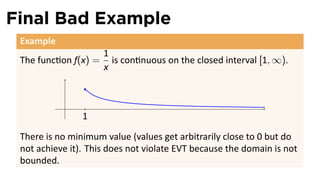
![Bad Example #1
Example
Consider the func on
{
x 0≤x<1 .
f(x) = |
x − 2 1 ≤ x ≤ 2. 1
Then although values of f(x) get arbitrarily close to 1 and never
bigger than 1, 1 is not the maximum value of f on [0, 1] because it is
never achieved.](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-23-320.jpg)
![Bad Example #1
Example
Consider the func on
{
x 0≤x<1 .
f(x) = |
x − 2 1 ≤ x ≤ 2. 1
Then although values of f(x) get arbitrarily close to 1 and never
bigger than 1, 1 is not the maximum value of f on [0, 1] because it is
never achieved. This does not violate EVT because f is not
con nuous.](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-24-320.jpg)







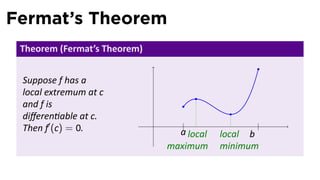
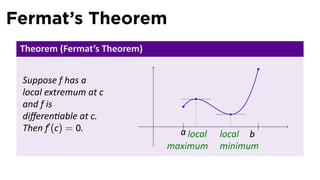












![Flowchart for placing extrema
Thanks to Fermat
Suppose f is a c is a
.
start
con nuous local max
func on on
the closed,
bounded Is c an
no Is f diff’ble no f is not
interval endpoint? at c? diff at c
[a, b], and c is
a global
yes yes
maximum
c = a or
point. f′ (c) = 0
c = b](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-50-320.jpg)
![The Closed Interval Method
This means to find the maximum value of f on [a, b], we need to:
Evaluate f at the endpoints a and b
Evaluate f at the cri cal points or cri cal numbers x where
either f′ (x) = 0 or f is not differen able at x.
The points with the largest func on value are the global
maximum points
The points with the smallest or most nega ve func on value
are the global minimum points.](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-51-320.jpg)

![Extreme values of a linear function
Example
Find the extreme values of f(x) = 2x − 5 on [−1, 2].](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-53-320.jpg)
![Extreme values of a linear function
Example
Find the extreme values of f(x) = 2x − 5 on [−1, 2].
Solu on
Since f′ (x) = 2, which is never
zero, we have no cri cal points
and we need only inves gate
the endpoints:
f(−1) = 2(−1) − 5 = −7
f(2) = 2(2) − 5 = −1](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-54-320.jpg)
![Extreme values of a linear function
Example
Find the extreme values of f(x) = 2x − 5 on [−1, 2].
Solu on
So
Since f′ (x) = 2, which is never
zero, we have no cri cal points The absolute minimum
and we need only inves gate (point) is at −1; the
the endpoints: minimum value is −7.
f(−1) = 2(−1) − 5 = −7 The absolute maximum
(point) is at 2; the
f(2) = 2(2) − 5 = −1
maximum value is −1.](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-55-320.jpg)
![Extreme values of a quadratic
function
Example
Find the extreme values of f(x) = x2 − 1 on [−1, 2].](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-56-320.jpg)
![Extreme values of a quadratic
function
Example
Find the extreme values of f(x) = x2 − 1 on [−1, 2].
Solu on
We have f′ (x) = 2x, which is zero when x = 0.](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-57-320.jpg)
![Extreme values of a quadratic
function
Example
Find the extreme values of f(x) = x2 − 1 on [−1, 2].
Solu on
We have f′ (x) = 2x, which is zero when x = 0. So our points to
check are:
f(−1) =
f(0) =
f(2) =](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-58-320.jpg)
![Extreme values of a quadratic
function
Example
Find the extreme values of f(x) = x2 − 1 on [−1, 2].
Solu on
We have f′ (x) = 2x, which is zero when x = 0. So our points to
check are:
f(−1) = 0
f(0) =
f(2) =](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-59-320.jpg)
![Extreme values of a quadratic
function
Example
Find the extreme values of f(x) = x2 − 1 on [−1, 2].
Solu on
We have f′ (x) = 2x, which is zero when x = 0. So our points to
check are:
f(−1) = 0
f(0) = − 1
f(2) =](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-60-320.jpg)
![Extreme values of a quadratic
function
Example
Find the extreme values of f(x) = x2 − 1 on [−1, 2].
Solu on
We have f′ (x) = 2x, which is zero when x = 0. So our points to
check are:
f(−1) = 0
f(0) = − 1
f(2) = 3](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-61-320.jpg)
![Extreme values of a quadratic
function
Example
Find the extreme values of f(x) = x2 − 1 on [−1, 2].
Solu on
We have f′ (x) = 2x, which is zero when x = 0. So our points to
check are:
f(−1) = 0
f(0) = − 1 (absolute min)
f(2) = 3](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-62-320.jpg)
![Extreme values of a quadratic
function
Example
Find the extreme values of f(x) = x2 − 1 on [−1, 2].
Solu on
We have f′ (x) = 2x, which is zero when x = 0. So our points to
check are:
f(−1) = 0
f(0) = − 1 (absolute min)
f(2) = 3 (absolute max)](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-63-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-64-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].
Solu on
Since f′ (x) = 6x2 − 6x = 6x(x − 1), we have cri cal points at x = 0
and x = 1.](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-65-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].
Solu on
Since f′ (x) = 6x2 − 6x = 6x(x − 1), we have cri cal points at x = 0
and x = 1. The values to check are](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-66-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].
Solu on
Since f′ (x) = 6x2 − 6x = 6x(x − 1), we have cri cal points at x = 0
and x = 1. The values to check are
f(−1) = − 4](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-67-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].
Solu on
Since f′ (x) = 6x2 − 6x = 6x(x − 1), we have cri cal points at x = 0
and x = 1. The values to check are
f(−1) = − 4
f(0) = 1](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-68-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].
Solu on
Since f′ (x) = 6x2 − 6x = 6x(x − 1), we have cri cal points at x = 0
and x = 1. The values to check are
f(−1) = − 4
f(0) = 1
f(1) = 0](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-69-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].
Solu on
Since f′ (x) = 6x2 − 6x = 6x(x − 1), we have cri cal points at x = 0
and x = 1. The values to check are
f(−1) = − 4
f(0) = 1
f(1) = 0
f(2) = 5](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-70-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].
Solu on
Since f′ (x) = 6x2 − 6x = 6x(x − 1), we have cri cal points at x = 0
and x = 1. The values to check are
f(−1) = − 4 (global min)
f(0) = 1
f(1) = 0
f(2) = 5](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-71-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].
Solu on
Since f′ (x) = 6x2 − 6x = 6x(x − 1), we have cri cal points at x = 0
and x = 1. The values to check are
f(−1) = − 4 (global min)
f(0) = 1
f(1) = 0
f(2) = 5 (global max)](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-72-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].
Solu on
Since f′ (x) = 6x2 − 6x = 6x(x − 1), we have cri cal points at x = 0
and x = 1. The values to check are
f(−1) = − 4 (global min)
f(0) = 1 (local max)
f(1) = 0
f(2) = 5 (global max)](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-73-320.jpg)
![Extreme values of a cubic function
Example
Find the extreme values of f(x) = 2x3 − 3x2 + 1 on [−1, 2].
Solu on
Since f′ (x) = 6x2 − 6x = 6x(x − 1), we have cri cal points at x = 0
and x = 1. The values to check are
f(−1) = − 4 (global min)
f(0) = 1 (local max)
f(1) = 0 (local min)
f(2) = 5 (global max)](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-74-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-75-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 .](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-76-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 . Then
5 4 1
f′ (x) = x2/3 + x−1/3 = x−1/3 (5x + 4)
3 3 3](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-77-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 . Then
5 4 1
f′ (x) = x2/3 + x−1/3 = x−1/3 (5x + 4)
3 3 3
Thus f′ (−4/5) = 0 and f is not differen able at 0. Thus there are two
cri cal points.](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-78-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 .
f(−1) =
f(−4/5) =
f(0) =
f(2) =](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-79-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 .
f(−1) = 1
f(−4/5) =
f(0) =
f(2) =](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-80-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 .
f(−1) = 1
f(−4/5) = 1.0341
f(0) =
f(2) =](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-81-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 .
f(−1) = 1
f(−4/5) = 1.0341
f(0) = 0
f(2) =](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-82-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 .
f(−1) = 1
f(−4/5) = 1.0341
f(0) = 0
f(2) = 6.3496](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-83-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 .
f(−1) = 1
f(−4/5) = 1.0341
f(0) = 0 (absolute min)
f(2) = 6.3496](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-84-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 .
f(−1) = 1
f(−4/5) = 1.0341
f(0) = 0 (absolute min)
f(2) = 6.3496 (absolute max)](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-85-320.jpg)
![Extreme values of an algebraic function
Example
Find the extreme values of f(x) = x2/3 (x + 2) on [−1, 2].
Solu on
Write f(x) = x5/3 + 2x2/3 .
f(−1) = 1
f(−4/5) = 1.0341 (rela ve max)
f(0) = 0 (absolute min)
f(2) = 6.3496 (absolute max)](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-86-320.jpg)
![Extreme values of another algebraic function
Example
√
Find the extreme values of f(x) = 4 − x2 on [−2, 1].](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-87-320.jpg)
![Extreme values of another algebraic function
Example
√
Find the extreme values of f(x) = 4 − x2 on [−2, 1].
Solu on
x
We have f′ (x) = − √ , which is zero when x = 0. (f is not
4 − x2
differen able at ±2 as well.)](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-88-320.jpg)
![Extreme values of another algebraic function
Example
√
Find the extreme values of f(x) = 4 − x2 on [−2, 1].
Solu on
x
We have f′ (x) = − √ , which is zero when x = 0. (f is not
4 − x2
differen able at ±2 as well.) So our points to check are:
f(−2) =](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-89-320.jpg)
![Extreme values of another algebraic function
Example
√
Find the extreme values of f(x) = 4 − x2 on [−2, 1].
Solu on
x
We have f′ (x) = − √ , which is zero when x = 0. (f is not
4 − x2
differen able at ±2 as well.) So our points to check are:
f(−2) = 0
f(0) =](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-90-320.jpg)
![Extreme values of another algebraic function
Example
√
Find the extreme values of f(x) = 4 − x2 on [−2, 1].
Solu on
x
We have f′ (x) = − √ , which is zero when x = 0. (f is not
4 − x2
differen able at ±2 as well.) So our points to check are:
f(−2) = 0
f(0) = 2
f(1) =](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-91-320.jpg)
![Extreme values of another algebraic function
Example
√
Find the extreme values of f(x) = 4 − x2 on [−2, 1].
Solu on
x
We have f′ (x) = − √ , which is zero when x = 0. (f is not
4 − x2
differen able at ±2 as well.) So our points to check are:
f(−2) = 0
f(0) = 2
√
f(1) = 3](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-92-320.jpg)
![Extreme values of another algebraic function
Example
√
Find the extreme values of f(x) = 4 − x2 on [−2, 1].
Solu on
x
We have f′ (x) = − √ , which is zero when x = 0. (f is not
4 − x2
differen able at ±2 as well.) So our points to check are:
f(−2) = 0 (absolute min)
f(0) = 2
√
f(1) = 3](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-93-320.jpg)
![Extreme values of another algebraic function
Example
√
Find the extreme values of f(x) = 4 − x2 on [−2, 1].
Solu on
x
We have f′ (x) = − √ , which is zero when x = 0. (f is not
4 − x2
differen able at ±2 as well.) So our points to check are:
f(−2) = 0 (absolute min)
f(0) = 2 (absolute max)
√
f(1) = 3](https://image.slidesharecdn.com/lesson18-maxmin011slides-110405071438-phpapp01/85/Lesson-18-Maximum-and-Minimum-Values-slides-94-320.jpg)
