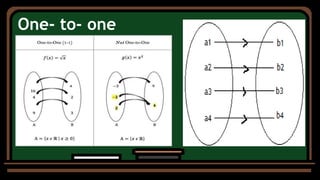
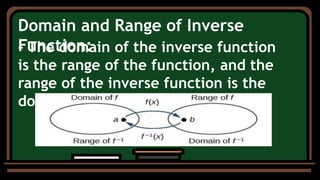
This document provides information about inverse functions including: - The inverse of a function is formed by reversing the coordinates of each ordered pair. A function has an inverse only if it is one-to-one. - The domain of the inverse function is the range of the original function, and the range of the inverse is the domain of the original. - To find the inverse of a one-to-one function, replace f(x) with y, interchange x and y, then solve for y in terms of x and replace y with f^-1(x). - Several examples are provided to demonstrate finding the inverse of different one-to-one functions by following the given steps.

1. Inverse Function
Prepared by: Mr. George G.
Lescano

2. Learning
Objectives:
At the end of the lesson you will
be able to:
- Determine the inverse of a one- to-
one functions.
- Represent an inverse function
through it’s: table of values and
graphs.
- Find the domain and range of an
inverse function.

3. What is a Inverse
Function?
- A set of ordered pairs formed by
reversing the coordinates of each
ordered pair of the function.
- Remember that function ‘’ f ‘’ has
an inverse if and only if ‘’ f ‘’ is one-
to- one function.
NOTE: Not every function has an
inverse.

4. Domain and Range of Inverse
Function:
- The domain of the inverse function
is the range of the function, and the
range of the inverse function is the
domain of the function.

5. Concept
check:
- A function y = f(x) is one- to- one if a
horizontal line drawn through the graph
of the function intersects the graph at
exactly one point.
- If the horizontal line intersects the
graph in more than one point, then the
function is not one- to- one. This test is
called geometric test for a one- to- one

6. Concept
check:
A function y = f(x) is said to be one-
to- one if:
− 𝑎 ≠ 𝑏 𝑖𝑚𝑝𝑙𝑖𝑒𝑠 𝑓 𝑎 ≠ 𝑓 𝑏 𝑤ℎ𝑒𝑛𝑒𝑣𝑒𝑟
𝑎 𝑎𝑛𝑑 𝑏 𝑎𝑟𝑒 𝑖𝑛 𝑡ℎ𝑒 𝑑𝑜𝑚𝑎𝑖𝑛 𝑜𝑓 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑓.
− 𝑇ℎ𝑒 𝑔𝑟𝑎𝑝ℎ 𝑜𝑓 𝑎 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛𝑠 𝑓 𝑎𝑛𝑑 𝑓−1𝑎𝑟𝑒
Symmetric with respect to the line y = x.

7. One- to- one
Function:
Recall that a
function is a set
of ordered pairs
in which no two
ordered pairs
have the same x
and have

8. One- to- one
Function:

9. One- to- one
Function:
𝑓 𝑥 = 0, 1 2, 3 4, 5 6, 7 8, 9 (10, 11)
𝑓 𝑥 = −1, 1 −2, 3 −4, 5 −6, 7 −8, 9

10. One- to- one
Function:
𝐴𝑣𝑒𝑛𝑔𝑒𝑟𝑠 𝑡𝑜 𝐽𝑢𝑠𝑡𝑖𝑐𝑒 𝐿𝑒𝑎𝑔𝑢𝑒
Marvel (x) Justice League
(y)
Hulk Superman
Thor Flash
Captain
America
Batman

11. One- to- one
Function:
𝑓 𝑥 = 5𝑥 − 8
x y
0 - 8
1 - 3
2 2
3 7
4 12

12. One- to- one
Function:
𝑓 𝑥 =
𝑥 + 1
2𝑥
x y
0 undefin
ed
1 1
2 3/ 4
3 2/ 3
4 5/ 8

13. One- to- one
Function:

14. Tell whether the following is a one-
to- one function or not.
𝟏. 𝒇 𝒙 = −𝟐, −𝟑 −𝟏, −𝟏 𝟎, 𝟏 𝟏, 𝟑 𝟐, 𝟓
𝑨𝒏𝒔𝒘𝒆𝒓: 𝑶𝒏𝒆 − 𝒕𝒐 − 𝒐𝒏𝒆
𝟐. 𝒇 𝒙 = 𝟎, −𝟕 𝟏, −𝟒 𝟎, 𝟏 𝟐, −𝟏 −𝟒, 𝟏
𝑨𝒏𝒔𝒘𝒆𝒓: 𝑵𝒐𝒕 𝒐𝒏𝒆 − 𝒕𝒐 − 𝒐𝒏𝒆

15. 𝑨𝒏𝒔𝒘𝒆𝒓: 𝑵𝒐𝒕 𝒐𝒏𝒆 − 𝒕𝒐 − 𝒐𝒏𝒆

16. 𝑨𝒏𝒔𝒘𝒆𝒓: 𝑶𝒏𝒆 − 𝒕𝒐 − 𝒐𝒏𝒆

17. Solving Inverse of a One- to-
one Function

18. Steps in solving Inverse of a One- to-
one Function:
STEP 1: Replace f (x) by y.
STEP 2: Interchange x and y.
STEP 3: Solve for y in terms of x.
STEP 4: Replace y with 𝒇−𝟏
𝒙 .

19. Example 1: 𝐟 𝒙 = 𝟐𝒙 + 𝟒
STEP 1: Replace f
(x) by y.
𝒚 = 𝟐𝒙 + 𝟒
STEP 2: Interchange
x and y.
𝒙 = 𝟐𝒚 + 𝟒
STEP 3: Solve for y
in terms of x.
(−𝟐𝒚 = −𝒙 + 𝟒)(−𝟏)
𝟐𝒚 = 𝒙 − 𝟒)
𝟐
𝒚 =
𝟏
𝟐
𝒙 − 𝟐
STEP 4: Replace y with
𝒇−𝟏 𝒙 .
𝒇−𝟏
𝒙 =
𝟏
𝟐
𝒙 − 𝟐

20. Example 2: 𝐟 𝒙 =
𝟐𝒙+𝟓
𝟑𝒙−𝟏
𝒚 =
𝟐𝒙 + 𝟓
𝟑𝒙 − 𝟏
𝒙 =
𝟐𝒚 + 𝟓
𝟑𝒚 − 𝟏
𝒙(𝟑𝒚 − 𝟏) = (𝟏)𝟐𝒚 + 𝟓
𝟑𝒙𝒚 − 𝒙 = 𝟐𝒚 + 𝟓
𝟑𝒙𝒚 − 𝟐𝒚 = 𝒙 + 𝟓
𝒚(𝟑𝒙 − 𝟐) = 𝒙 + 𝟓
𝟑𝒙 − 𝟐
𝒚 =
𝒙 + 𝟓
𝟑𝒙 − 𝟐
𝒇−𝟏
𝒙 =
𝒙 + 𝟓
𝟑𝒙 − 𝟐

21. Example 3: 𝐟 𝒙 =
𝟐𝒙 − 𝟔
𝒚 = 𝟐𝒙 − 𝟔
𝒙 = 𝟐𝒚 − 𝟔
(𝒙)𝟐= (𝟐
𝟐𝒚 − 𝟔)𝟐
𝒙𝟐
= 𝟐𝒚 − 𝟔
𝟐
𝒙𝟐
+ 𝟔 = 𝟐𝒚
𝒚 =
𝒙𝟐
+ 𝟔
𝟐
𝒇−𝟏 𝒙 =
𝟏
𝟐
𝒙𝟐 + 𝟑

22. Example
4: x y
0 2
1 1
2 - 4
3 0
4 - 2
x y
2 0
1 1
-4 2
0 3
-2 4

23. Example
5:
X Y
- 1 0
1 2
3 4
X Y
0 -1
2 1
4 3

24. Your Turn: Solve for the following
inverse.
1. 𝐟 𝒙 = 𝟓𝒙 + 𝟐
𝟑. 𝐟 𝒙 =
𝟐𝒙
𝟑𝒙 − 𝟏
2. 𝐟 𝒙 =
𝟐
𝟑+𝒙

25. Your Turn: Solve for the following
inverse.
1. 𝐟 𝒙 = 𝟓𝒙 + 𝟐
𝒇−𝟏
𝒙 =
𝒙 − 𝟐
𝟓

26. Your Turn: Solve for the following
inverse.
2. 𝐟 𝒙 =
𝟐
𝟑+𝒙
𝒇−𝟏 𝒙 = −𝟑 +
𝟐
𝒙

27. Your Turn: Solve for the following
inverse.
𝟑. 𝐟 𝒙 =
𝟐𝒙
𝟑𝒙 − 𝟏
𝒇−𝟏
𝒙 =
𝒙
𝟑𝒙 − 𝟐

28. Picture of the
day!