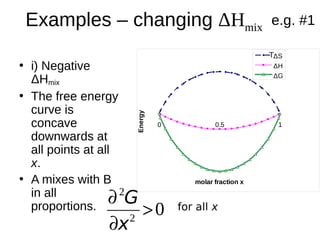
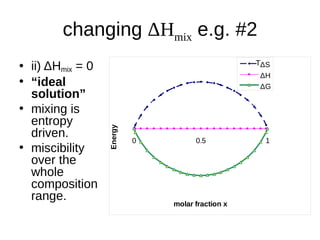
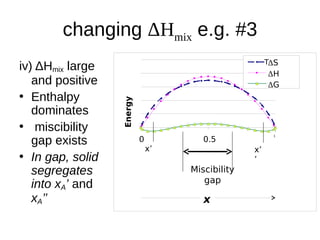
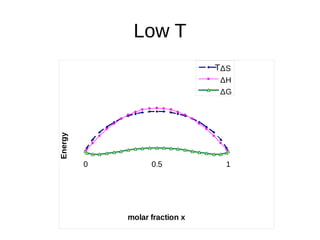
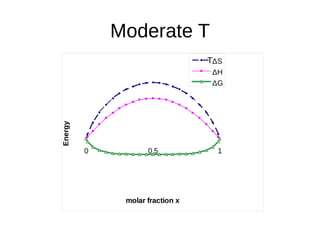
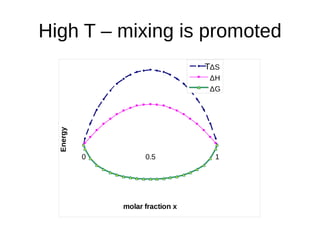
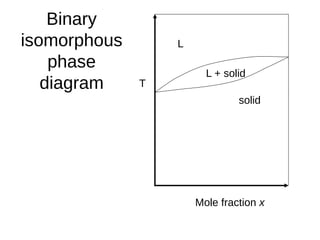
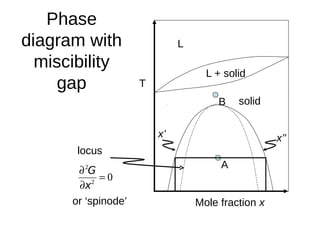
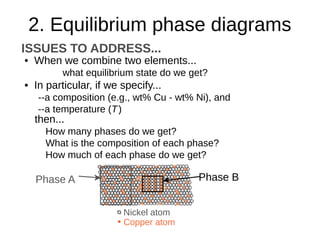
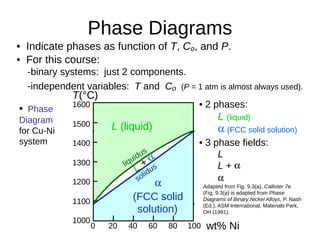
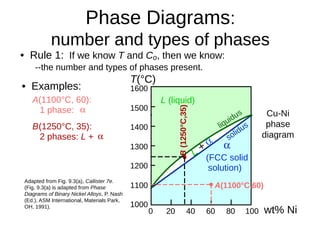
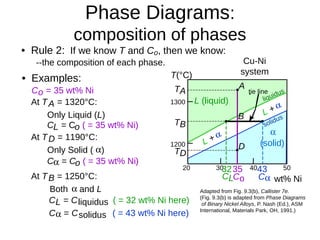
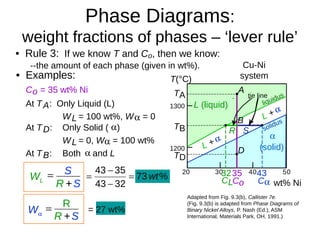
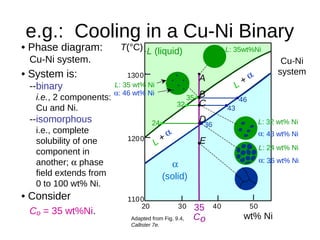
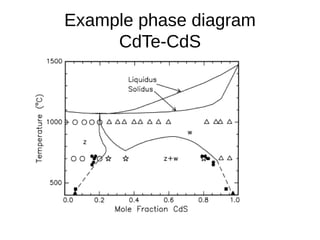
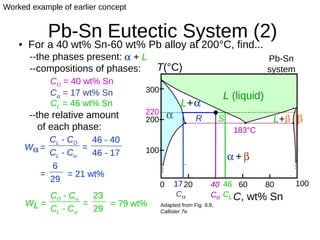
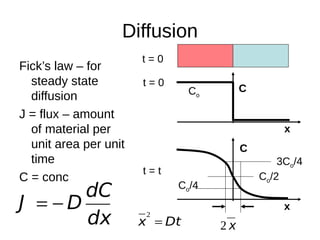
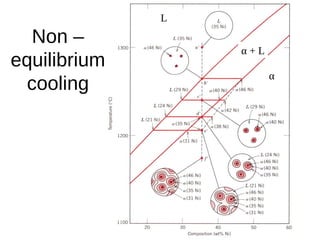
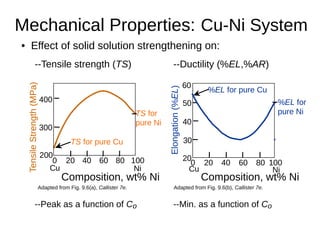
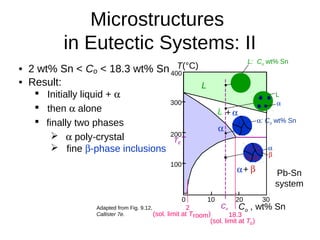
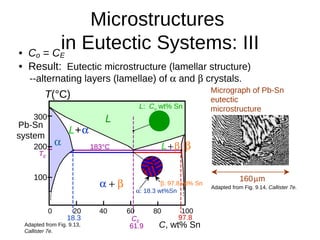
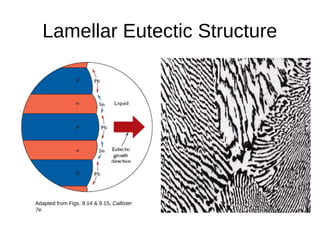
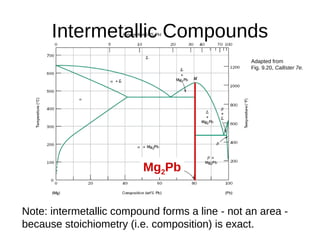
1. The document discusses phase diagrams and thermodynamics of mixing. 2. It explains how phase diagrams can be used to determine the number and types of phases present, the composition of each phase, and the amount of each phase at a given temperature and composition. 3. Binary eutectic and eutectoid systems allow for a range of microstructures depending on the cooling rate, and alloying generally increases strength but decreases ductility due to solid solution strengthening.

2. Learning objectives
2 Phase diagrams
Be able to read a phase
diagram
Be able to identify the phases
present at a given point
Be able to calculate how much
of those phases there are
Be able to predict the
microstructures from the phase
diagram
3 Mixing
Understand the thermodynamic
basis of mixing
Understand the origin of the
miscibility gap
Be able to use the phase
diagram to predict miscibility
phenomena
1.Solid state reactions
Recap: how Gibbs Free Energy
can be used to predict reactions
There will be worked
examples on this bit
for you to practice ….

3. 1. Prediction of reactions
e.g. solar cell contact – metal M to semiconductor AB
AB
M
AB
M
MB + A
AB
M
or
stable
unstable
M + AB  MB + A Will it happen at equilibrium?
keqm = [MB]*[A] /[M]*[AB] If keqm is large, the reaction goes from l to r
)ln( eqmkRTG Find the Gibb’s free energy for the reaction.
If ∆G is large and negative, keqm is large and the reaction goes from l to r

4. 1. Prediction of reactions
initialfinalreaction
initialfinalreaction
initialfinalreaction
reactionreactionreaction
SSS
HHH
GGG
STHG




M + AB  MB + A
etc
GGGGG ABMAMBreaction )()( 
If ∆G is large and negative, keqm is large and the reaction goes f
In this case the contact would be unstable to reaction with the solar cell
materials. The contact could become non-Ohmic, the series resistance
could increase, and the performance could become unstable.

5. ISSUES TO ADDRESS...
• When we combine two elements...
what equilibrium state do we get?
• In particular, if we specify...
--a composition (e.g., wt% Cu - wt% Ni), and
--a temperature (T)
then...
How many phases do we get?
What is the composition of each phase?
How much of each phase do we get?
2. Equilibrium phase diagrams
Phase BPhase A
Nickel atom
Copper atom

6. • Components:
The elements or compounds which are present in the mixture
(e.g., Al and Cu)
• Phases:
The physically and chemically distinct material regions
that result (e.g.,  and ).
Aluminum-
Copper
Alloy
Components and Phases
(darker
phase)
 (lighter
phase)
Adapted from
chapter-opening
photograph,
Chapter 9,
Callister 3e.

7. Phase Equilibria
Crystal
Structure
electroneg r (nm)
Ni FCC 1.9 0.1246
Cu FCC 1.8 0.1278
• Both have the same crystal structure (FCC) and have
similar electronegativities and atomic radii (W. Hume –
Rothery rules) suggesting high mutual solubility.
Simple solution system (e.g., Ni-Cu solution)
• Ni and Cu are totally miscible in all proportions.

8. Phase Diagrams
• Indicate phases as function of T, Co, and P.
• For this course:
-binary systems: just 2 components.
-independent variables: T and Co (P = 1 atm is almost always used).
• Phase
Diagram
for Cu-Ni
system
Adapted from Fig. 9.3(a), Callister 7e.
(Fig. 9.3(a) is adapted from Phase
Diagrams of Binary Nickel Alloys, P. Nash
(Ed.), ASM International, Materials Park,
OH (1991).
• 2 phases:
L (liquid)
 (FCC solid solution)
• 3 phase fields:
L
L + 

wt% Ni20 40 60 80 1000
1000
1100
1200
1300
1400
1500
1600
T(°C)
L (liquid)

(FCC solid
solution)
L +liquidus
solidus

9. wt% Ni20 40 60 80 1000
1000
1100
1200
1300
1400
1500
1600
T(°C)
L (liquid)

(FCC solid
solution)
L
+ 
liquidus
solidus
Cu-Ni
phase
diagram
Phase Diagrams:
number and types of phases
• Rule 1: If we know T and Co, then we know:
--the number and types of phases present.
• Examples:
A(1100°C, 60):
1 phase: 
B(1250°C, 35):
2 phases: L + 
Adapted from Fig. 9.3(a), Callister 7e.
(Fig. 9.3(a) is adapted from Phase
Diagrams of Binary Nickel Alloys, P. Nash
(Ed.), ASM International, Materials Park,
OH, 1991).
B(1250°C,35) A(1100°C,60)

10. wt% Ni
20
1200
1300
T(°C)
L (liquid)

(solid)L +
liquidus
solidus
30 40 50
L +
Cu-Ni
system
Phase Diagrams:
composition of phases
• Rule 2: If we know T and Co, then we know:
--the composition of each phase.
• Examples:
TA
A
35
Co
32
CL
At TA = 1320°C:
Only Liquid (L)
CL = Co ( = 35 wt% Ni)
At TB = 1250°C:
Both  and L
CL = Cliquidus ( = 32 wt% Ni here)
C = Csolidus ( = 43 wt% Ni here)
At TD = 1190°C:
Only Solid ( )
C = Co ( = 35 wt% Ni)
Co = 35 wt% Ni
Adapted from Fig. 9.3(b), Callister 7e.
(Fig. 9.3(b) is adapted from Phase Diagrams
of Binary Nickel Alloys, P. Nash (Ed.), ASM
International, Materials Park, OH, 1991.)
B
TB
D
TD
tie line
4
C
3

11. • Rule 3: If we know T and Co, then we know:
--the amount of each phase (given in wt%).
• Examples:
At TA: Only Liquid (L)
WL = 100 wt%, W = 0
At TD: Only Solid ( )
WL = 0, W = 100 wt%
Co = 35 wt% Ni
Adapted from Fig. 9.3(b), Callister 7e.
(Fig. 9.3(b) is adapted from Phase Diagrams of
Binary Nickel Alloys, P. Nash (Ed.), ASM
International, Materials Park, OH, 1991.)
Phase Diagrams:
weight fractions of phases – ‘lever rule’
wt% Ni
20
1200
1300
T(°C)
L (liquid)

(solid)L +
liquidus
solidus
30 40 50
L +
Cu-Ni
system
TA
A
35
Co
32
CL
B
TB
D
TD
tie line
4
C
3
R S
At TB: Both  and L
%73
3243
3543
wt



= 27 wt%
WL
 S
R +S
W
 R
R +S

12. wt% Ni
20
1200
1300
30 40 50
1100
L (liquid)

(solid)
L +

L +

T(°C)
A
35
Co
L: 35wt%Ni
Cu-Ni
system
• Phase diagram:
Cu-Ni system.
• System is:
--binary
i.e., 2 components:
Cu and Ni.
--isomorphous
i.e., complete
solubility of one
component in
another;  phase
field extends from
0 to 100 wt% Ni.
Adapted from Fig. 9.4,
Callister 7e.
• Consider
Co = 35 wt%Ni.
e.g.: Cooling in a Cu-Ni Binary
4635
43
32
: 43 wt% Ni
L: 32 wt% Ni
L: 24 wt% Ni
: 36 wt% Ni
B: 46 wt% Ni
L: 35 wt% Ni
C
D
E
24 36

13. Equilibrium cooling
• The compositions that freeze are a
function of the temperature
• At equilibrium, the ‘first to freeze’
composition must adjust on further cooling
by solid state diffusion
• We now examine diffusion processes –
how fast does diffusion happen in the solid
state?

14. Diffusion
Fick’s law – for
steady state
diffusion
J = flux – amount
of material per
unit area per unit
time
C = conc
dx
dC
DJ 
C
x
Co
C
x
Co/4
Co/2
3Co/4
x2
t = 0
t = 0
t = t
Dtx 
2

15. Diffusion cont….
• Diffusion coefficient D (cm2s-1)
• Non-steady state diffusion
Fick’s second law
• Diffusion is thermally activated







RT
Q
DD d
exp0
2
2
x
C
D
t
C






16. Non –
equilibrium
cooling
α
L
α + L

17. • C changes as we solidify.
• Cu-Ni case:
• Fast rate of cooling:
Cored structure
• Slow rate of cooling:
Equilibrium structure
First  to solidify has C = 46 wt% Ni.
Last  to solidify has C = 35 wt% Ni.
Cored vs Equilibrium Phases
First  to solidify:
46 wt% Ni
Uniform C:
35 wt% Ni
Last  to solidify:
< 35 wt% Ni

18. Mechanical Properties: Cu-Ni System
• Effect of solid solution strengthening on:
--Tensile strength (TS) --Ductility (%EL,%AR)
--Peak as a function of Co --Min. as a function of Co
Adapted from Fig. 9.6(a), Callister 7e. Adapted from Fig. 9.6(b), Callister 7e.
TensileStrength(MPa)
Composition, wt% Ni
Cu Ni
0 20 40 60 80 100
200
300
400
TS for
pure Ni
TS for pure Cu
Elongation(%EL) Composition, wt% Ni
Cu Ni
0 20 40 60 80 100
20
30
40
50
60
%EL for
pure Ni
%EL for pure Cu

19. : Min. melting TE
2 components
has a special composition
with a min. melting T.
Adapted from Fig. 9.7,
Callister 7e.
Binary-Eutectic Systems
• Eutectic transition
L(CE) (CE) + (CE)
• 3 single phase regions
(L,)
• Limited solubility:
: mostly Cu
: mostly Ag
• TE : No liquid below TE
• CE
composition
Ex.: Cu-Ag system
Cu-Ag
system
L (liquid)
 L + 
L+

Co wt% Ag in Cu/Ag alloy
20 40 60 80 1000
200
1200
T(°C)
400
600
800
1000
CE
TE 8.0 71.9 91.2
779°C

20. L+
L+
 + 
200
T(°C)
18.3
C, wt% Sn
20 60 80 1000
300
100
L (liquid)
 183°C
61.9 97.8

• For a 40 wt% Sn-60 wt% Pb alloy at 150°C, find...
--the phases present: Pb-Sn
system
e.g. Pb-Sn Eutectic System (1)
 + 
--compositions of phases:
CO = 40 wt% Sn
--the relative amount
of each phase:
150
40
Co
11
C
99
C
SR
C = 11 wt% Sn
C = 99 wt% Sn
W=
C - CO
C - C
=
99 - 40
99 - 11
=
59
88
= 67 wt%
S
R+S
=
W =
CO - C
C - C
=
R
R+S
=
29
88
= 33 wt%=
40 - 11
99 - 11
Adapted from Fig. 9.8,
Callister 7e.

21. • 2 wt% Sn < Co < 18.3 wt% Sn
• Result:
 Initially liquid + 
 then  alone
finally two phases
 poly-crystal
 fine -phase inclusions
Adapted from Fig. 9.12,
Callister 7e.
Microstructures
in Eutectic Systems: II
Pb-Sn
system
L + 
200
T(°C)
Co , wt% Sn
10
18.3
200
Co
300
100
L

30
+ 
400
(sol. limit at TE)
TE
2
(sol. limit at Troom)
L

L: Co wt% Sn


: Co wt% Sn

23. Lamellar Eutectic Structure
Adapted from Figs. 9.14 & 9.15, Callister
7e.

24. Intermetallic Compounds
Mg2Pb
Note: intermetallic compound forms a line - not an area -
because stoichiometry (i.e. composition) is exact.
Adapted from
Fig. 9.20, Callister 7e.

25. Eutectoid & Peritectic
Cu-Zn Phase diagram
Adapted from
Fig. 9.21, Callister 7e.
Eutectoid transition   + 
Peritectic transition  + L 

26. • Phase diagrams are useful tools to determine:
--the number and types of phases,
--the wt% of each phase,
--and the composition of each phase
for a given T and composition of the system.
• Alloying to produce a solid solution usually
--increases the tensile strength (TS)
--decreases the ductility.
• Binary eutectics and binary eutectoids allow for
a range of microstructures.
Summary

27. 3)Thermodynamics of mixing
• Why do some things mix and others
not?
• Why does heating promote mixing?
• Is an alloy of two semiconductors a
random solid solution, or is it just a
mixture of two phases?
Solid solution Mixture of phases ?OR

28. Free energy of mixing
• Enthalpy term – bond energies
• Entropy term – stats of mixing
 behaviour of mixtures 
consider the case: Pure A + Pure B 
mixture AxB1-x
mixmixmix STHG 

29. Enthalpy term: Compare the energy
in bonds (VAB etc) before and after
mixing
Heat of mixing Binding energy
in mixture
compared to
average in
components
Binding
energy
change on
mixing
ΔHmix
Exothermic VAB
> 1/2(VAA
+ VBB
) Stronger -ve
Ideal VAB
= 1/2(VAA
+ VBB
) Same 0
endothermic VAB
< 1/2(VAA
+ VBB
) Weaker +ve

30. ΔHmix derived
ΔHmix = (H for mixture AB) – (H for pure A + H for pure B)
• ΔHmix = zNxA xB {1/2(VAA + VBB) – VAB}
NAA etc = number of bonds of type
AA, AB etc
NA, NB, number of atoms of A, B. NA
+ NB = N
VAA, VBB, VAB, = binding energies of
pairs A-A,
xA etc = NA/N = mole fraction of A
For reference only

31. ΔSmix derived
ΔS = (Sfinal – Sinitial)
Sfinal from the statistical definition S = kBlnw
ΔSmix = kBln
Using Stirling’s approximation lnn! = nlnn-n gives
• ΔSmix = -NkB[ xAlnxA + xBlnxB]
)!()!(
!
BA NxNx
N
For reference only

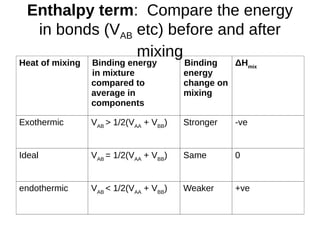
32. ΔGmix - the formula
• ΔGmix = zNxA xB {1/2(VAA + VBB) – VAB}
+ NkBT[ xAlnxA + xBlnxB]
Binding energy term {...} may be +ve or –ve
Entropy term [...] is negative
mixmixmix STHG 
For reference only

35. changing ΔHmix e.g. #3
iv) ΔHmix large
and positive
• Enthalpy
dominates
• miscibility
gap exists
• In gap, solid
segregates
into xA’ and
xA’’
0 0.5
1
Energy
ΔS
ΔH
ΔG
x’ x’
’
Miscibility
gap
x
T

39. Binary
isomorphous
phase
diagram
Mole fraction x
T
L
L + solid
solid

40. Phase
diagram with
miscibility
gap
Mole fraction x
T
L
L + solid
solid
x’ x’’
02
2



x
G
locus
or ‘spinode’
A
B

41. Example phase diagram
CdTe-CdS

42. L+
 + 
200
T(°C)
C, wt% Sn
20 60 80 1000
300
100
L (liquid)
 
L+
183°C
• For a 40 wt% Sn-60 wt% Pb alloy at 200°C, find...
--the phases present: Pb-Sn
system
Adapted from Fig. 9.8,
Callister 7e.
Pb-Sn Eutectic System (2)
 + L
--compositions of phases:
CO = 40 wt% Sn
--the relative amount
of each phase:
W =
CL - CO
CL - C
=
46 - 40
46 - 17
=
6
29
= 21 wt%
WL =
CO - C
CL - C
=
23
29
= 79 wt%
40
Co
46
CL
17
C
220
SR
C = 17 wt% Sn
CL = 46 wt% Sn
Worked example of earlier concept