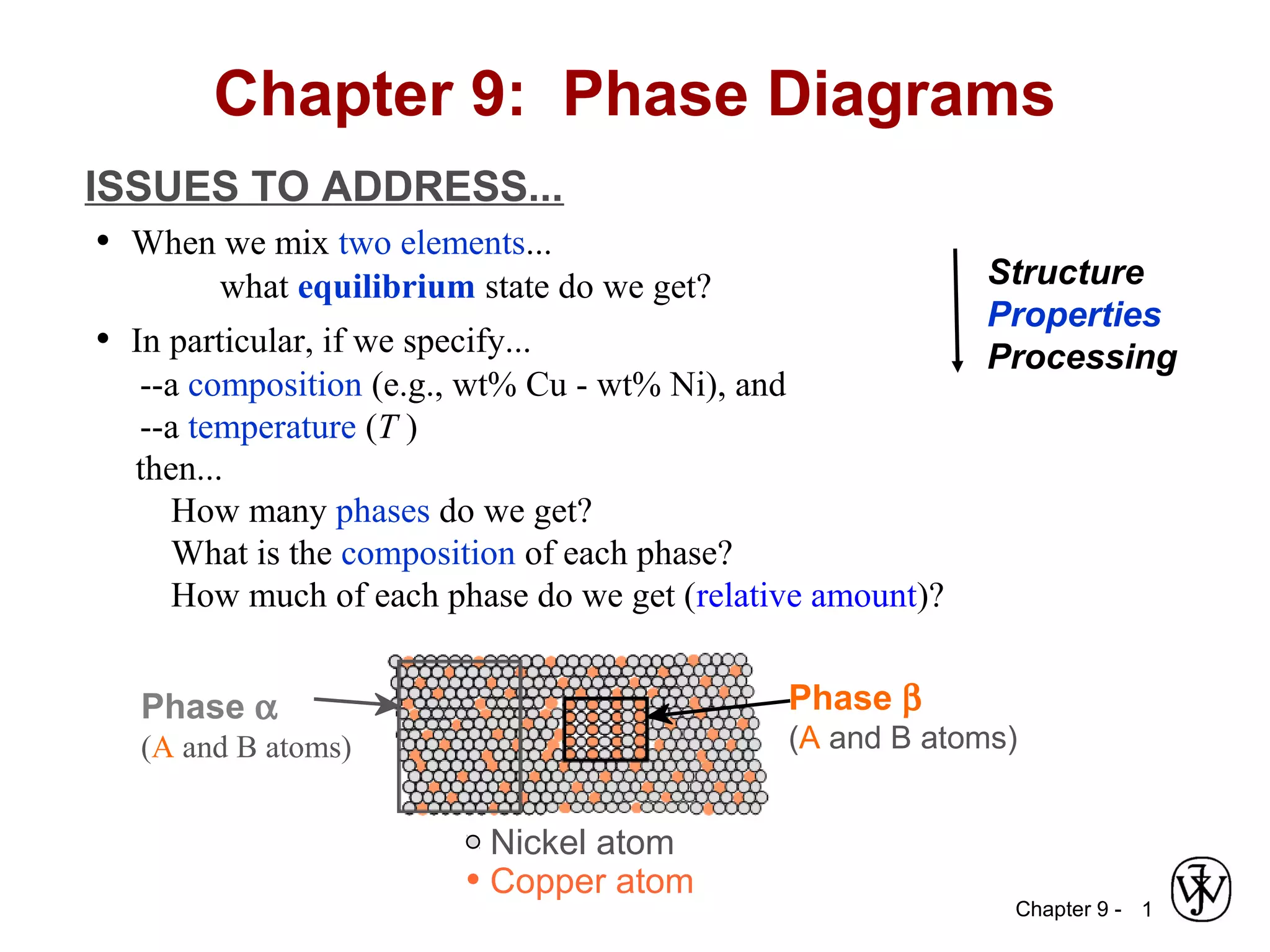
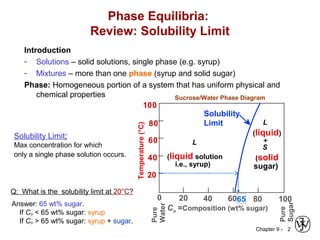
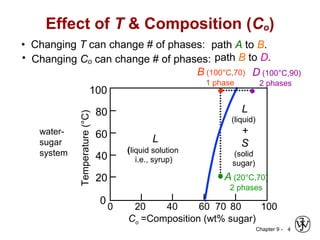
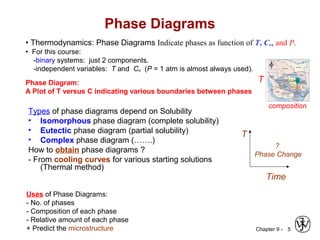
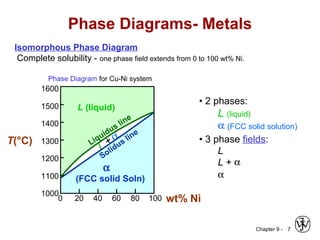
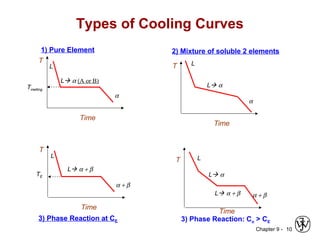
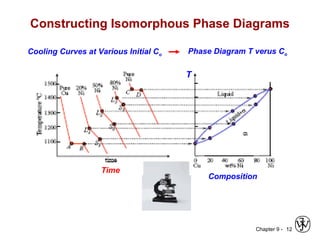
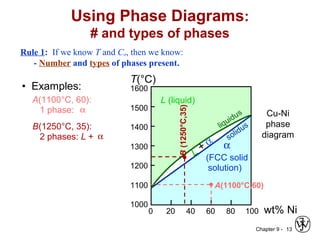
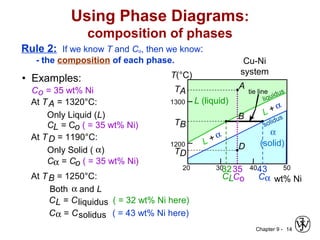
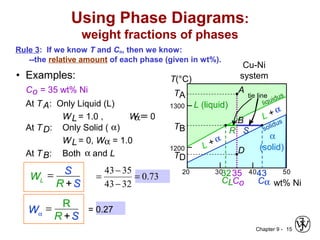
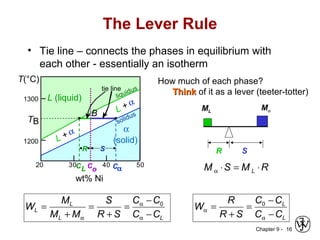
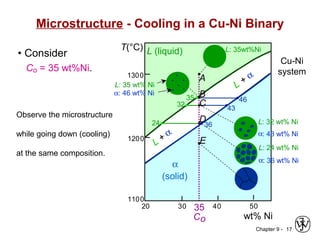
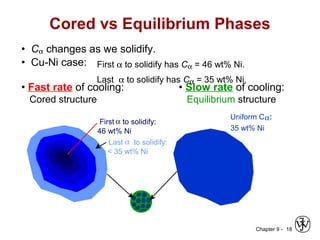
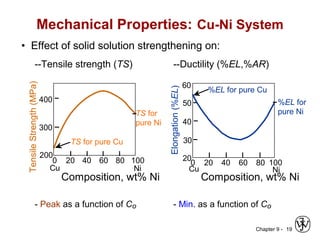
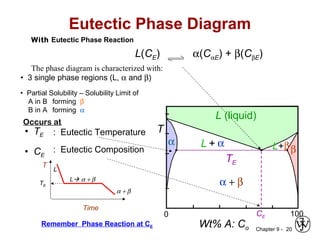
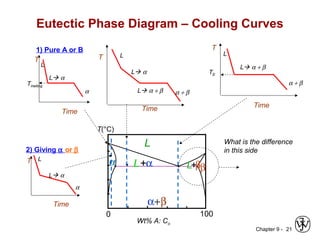
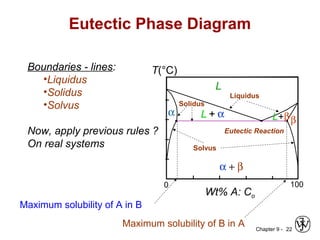
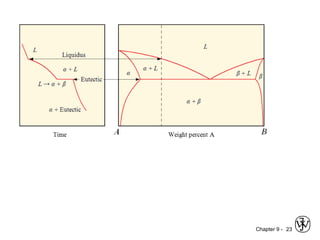
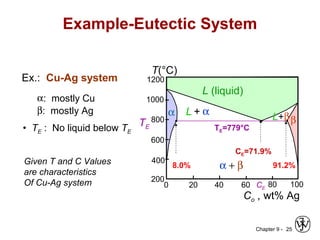
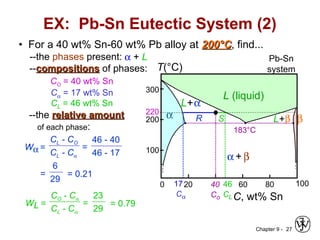
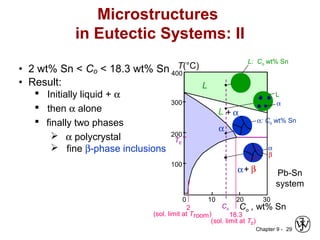
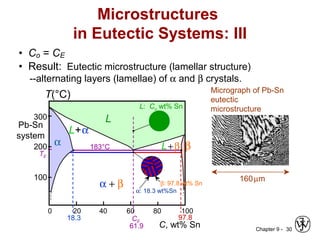
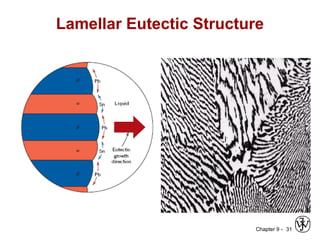
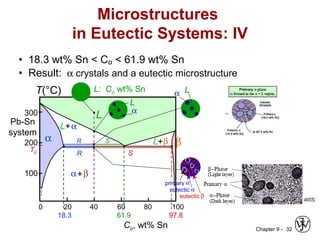
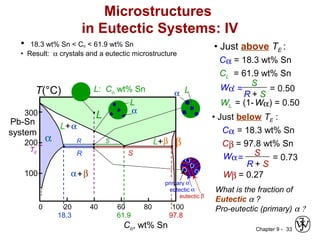
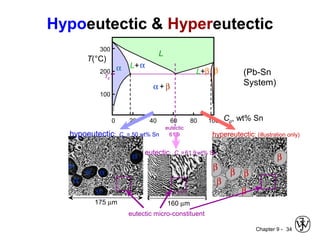
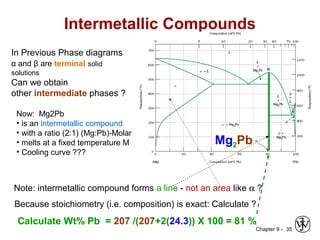
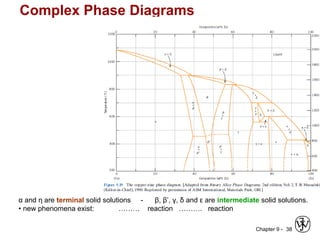
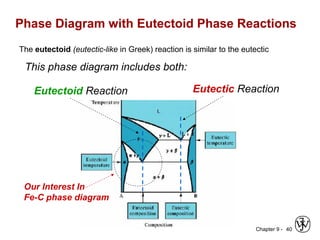
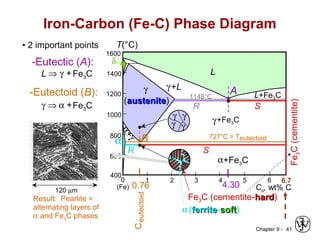
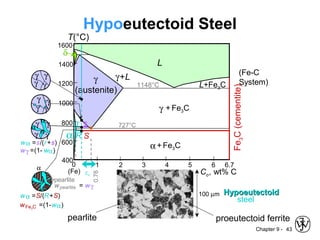
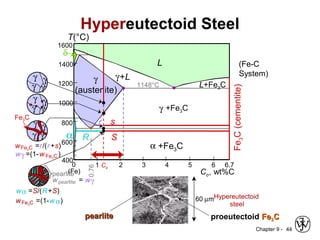
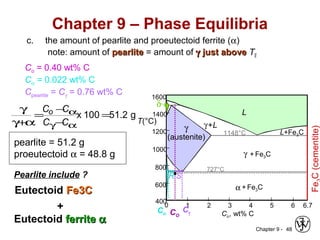
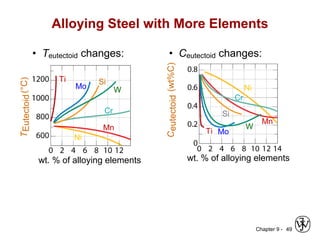
This document discusses phase diagrams and related concepts. It begins by asking questions about what equilibrium state and phases result from mixing two elements at a given composition and temperature. It then provides information on phase diagrams, including how they are constructed using cooling curve data from mixtures at different compositions. It discusses rules for determining phase information like number, composition, and amounts from a phase diagram given temperature and composition. Finally, it gives examples of an isomorphous system and eutectic system phase diagram.

1. Chapter 9 - 1
ISSUES TO ADDRESS...
• When we mix two elements...
what equilibrium state do we get?
• In particular, if we specify...
--a composition (e.g., wt% Cu - wt% Ni), and
--a temperature (T )
then...
How many phases do we get?
What is the composition of each phase?
How much of each phase do we get (relative amount)?
Chapter 9: Phase Diagrams
Phase β
(A and B atoms)
Phase α
(A and B atoms)
Nickel atom
Copper atom
Structure
Properties
Processing

2. Chapter 9 - 2
Phase Equilibria:
Review: Solubility Limit
Introduction
- Solutions – solid solutions, single phase (e.g. syrup)
- Mixtures – more than one phase (syrup and solid sugar)
Phase: Homogeneous portion of a system that has uniform physical and
chemical properties
Solubility Limit:
Max concentration for which
only a single phase solution occurs.
Q: What is the solubility limit at 20°C?
Answer: 65 wt% sugar.
If Co < 65 wt% sugar: syrup
If Co > 65 wt% sugar: syrup + sugar.
65
Sucrose/Water Phase Diagram
Pure
Sugar
Temperature(°C)
0 20 40 60 80 100
Co =Composition (wt% sugar)
L
(liquid solution
i.e., syrup)
Solubility
Limit L
(liquid)
+
S
(solid
sugar)
20
40
60
80
100
Pure
Water

3. Chapter 9 - 3
• Components:
The elements or compounds which are present in the mixture (e.g., Al and Cu)
• Phases:
The physically and chemically distinct material regions that result (e.g., α and β).
•Equilibrium
No change with time – fixed composition for each component
Al-Cu Alloy
Components and Phases
α (darker phase)
Includes Al and Cu
β (lighter phase)
Includes Al and Cu
Two phases
Two Components

4. Chapter 9 - 4
Effect of T & Composition (Co)
• Changing T can change # of phases:
D (100°C,90)
2 phases
B (100°C,70)
1 phase
path A to B.
• Changing Co can change # of phases: path B to D.
A (20°C,70)
2 phases
70 80 1006040200
Temperature(°C)
Co =Composition (wt% sugar)
L
(liquid solution
i.e., syrup)
20
100
40
60
80
0
L
(liquid)
+
S
(solid
sugar)
water-
sugar
system

5. Chapter 9 - 5
Phase Diagrams
Types of phase diagrams depend on Solubility
• Isomorphous phase diagram (complete solubility)
• Eutectic phase diagram (partial solubility)
• Complex phase diagram (…….)
How to obtain phase diagrams ?
- From cooling curves for various starting solutions
(Thermal method)
• Thermodynamics: Phase Diagrams Indicate phases as function of T, Co, and P.
• For this course:
-binary systems: just 2 components.
-independent variables: T and Co (P = 1 atm is almost always used).
Phase Diagram:
A Plot of T versus C indicating various boundaries between phases
T
Time
?
Phase Change
T
composition
Uses of Phase Diagrams:
- No. of phases
- Composition of each phase
- Relative amount of each phase
+ Predict the microstructure

6. Chapter 9 - 6
Phase Equilibria - Solutions
Crystal
Structure
electroneg r (nm)
Ni FCC 1.9 0.1246
Cu FCC 1.8 0.1278
Both metals have
•Nearly the same atomic radius
•The same crystal structure (FCC)
•similar electronegativities
(W. Hume – Rothery rules) suggesting high mutual solubility.
Simple Solution System (e.g., Ni-Cu solution)
Remember
Ni and Cu are totally miscible (soluble) in all proportions (compositions).
ONE PHASE ALWAYS – Isomorphous !

7. Chapter 9 - 7
Phase Diagrams- Metals
• 2 phases:
L (liquid)
α (FCC solid solution)
• 3 phase fields:
L
L + α
α
Phase Diagram for Cu-Ni system
20 40 60 80 1000 wt% Ni
1000
1100
1200
1300
1400
1500
1600
T(°C)
L (liquid)
α
(FCC solid Soln)
L +αLiquidus line
Solidus line
Isomorphous Phase Diagram
Complete solubility - one phase field extends from 0 to 100 wt% Ni.

8. Chapter 9 - 8
Phase Change
• Phase boundary:
Lines between different phases e.g.
– Liquid
– solid
• one phase
• two phases …etc)
• Phase Change:
– Solidification (or melting)
– Phase Reaction: one phase gives DIRECTLY two phases
e.g.
Liquid  Solid phase 1 + Solid Phase 2 (both insoluble)
• This occurs at
– Certain (fixed) temperature: TE
– Certain (fixed) composition: CE
• Eutectic Phase Reaction:
L α + β
• There are other types of phase reactions (Later)

9. Chapter 9 - 9
Cooling Curves
There are various types of cooling curves:
Depending on composition (characteristics)
1. Pure Element
2. Mixture of soluble 2 elements
3. Mixture of Partially Soluble 2 elements
4. Mixtures undergoing Phase Reactions
1. At the composition for phase reaction
2. Before the composition for phase reaction

10. Chapter 9 - 10
Types of Cooling Curves
2) Mixture of soluble 2 elements
Time
L
L α
α
T
3) Phase Reaction at CE 3) Phase Reaction: Co > CE
Time
L
L α + β α + β
T
L α
T
Time
L
L α (A or B)
α
1) Pure Element
Tmelting
Time
L
L α + β
α + β
T
TE

11. Chapter 9 - 11
Constructing Phase Diagrams
Thermal Method
• Start with several different solutions
• Each solution at certain co
• Prepare the solutions in liquid form (melting)
• Cool each solution while recording T versus time
• Plot the cooling curve for each solution
• At each phase change: there are changes in the slope
– Latent Heat
– Change in the properties (specific heat)
– Phase reaction (later)
• Project cooling curves on T versus co plot.
• Connect the points from projection creating boundaries.
• Label different obtained areas and boundaries.

12. Chapter 9 - 12
Constructing Isomorphous Phase Diagrams
Cooling Curves at Various Initial Co Phase Diagram T verus Co
T
Composition
Time

13. Chapter 9 - 13
wt% Ni20 40 60 80 1000
1000
1100
1200
1300
1400
1500
1600
T(°C)
L (liquid)
α
(FCC solid
solution)
L
+ α
liquidus
solidus
Cu-Ni
phase
diagram
Using Phase Diagrams:
# and types of phases
Rule 1: If we know T and Co, then we know:
- Number and types of phases present.
• Examples:
A(1100°C, 60):
1 phase: α
B(1250°C, 35):
2 phases: L + α
B(1250°C,35) A(1100°C,60)

14. Chapter 9 - 14
wt% Ni
20
1200
1300
T(°C)
L (liquid)
α
(solid)L +α
liquidus
solidus
30 40 50
L +α
Cu-Ni
system
Using Phase Diagrams:
composition of phases
Rule 2: If we know T and Co, then we know:
- the composition of each phase.
• Examples:
TA
A
35
Co
32
CL
At TA = 1320°C:
Only Liquid (L)
CL = Co ( = 35 wt% Ni)
At TB = 1250°C:
Both α and L
CL = Cliquidus ( = 32 wt% Ni here)
Cα = Csolidus ( = 43 wt% Ni here)
At TD = 1190°C:
Only Solid ( α)
Cα = Co ( = 35 wt% Ni)
Co = 35 wt% Ni
B
TB
D
TD
tie line
4
Cα
3

15. Chapter 9 - 15
Rule 3: If we know T and Co, then we know:
--the relative amount of each phase (given in wt%).
• Examples:
At TA: Only Liquid (L)
WL = 1.0 , W =α = 0
At TD: Only Solid ( α)
WL = 0, Wα = 1.0
Co = 35 wt% Ni
Using Phase Diagrams:
weight fractions of phases
wt% Ni
20
1200
1300
T(°C)
L (liquid)
α
(solid)L +α
liquidus
solidus
30 40 50
L +α
Cu-Ni
system
TA
A
35
Co
32
CL
B
TB
D
TD
tie line
4
Cα
3
R S
At TB: Both α and L
73.0
3243
3543
=
−
−
=
= 0.27
WL
= S
R +S
Wα
= R
R +S

16. Chapter 9 - 16
• Tie line – connects the phases in equilibrium with
each other - essentially an isotherm
The Lever Rule
How much of each phase?
ThinkThink of it as a lever (teeter-totter)
ML
Mα
R S
RMSM L ⋅=⋅α
L
L
LL
L
L
CC
CC
SR
R
W
CC
CC
SR
S
MM
M
W
−
−
=
+
=
−
−
=
+
=
+
=
α
α
α
α
α
00
wt% Ni
20
1200
1300
T(°C)
L (liquid)
α
(solid)L +α
liquidus
solidus
30 40 50
L +α
B
TB
tie line
CoCL Cα
SR

17. Chapter 9 - 17
wt% Ni
20
1200
1300
30 40 50
1100
L (liquid)
α
(solid)
L +
α
L +
α
T(°C)
A
35
Co
L: 35wt%Ni
Cu-Ni
system
Observe the microstructure
while going down (cooling)
at the same composition.
• Consider
Co = 35 wt%Ni.
Microstructure - Cooling in a Cu-Ni Binary
4635
43
32
α: 43 wt% Ni
L: 32 wt% Ni
L: 24 wt% Ni
α: 36 wt% Ni
Bα: 46 wt% Ni
L: 35 wt% Ni
C
D
E
24 36

18. Chapter 9 - 18
• Cα changes as we solidify.
• Cu-Ni case:
• Fast rate of cooling:
Cored structure
• Slow rate of cooling:
Equilibrium structure
First α to solidify has Cα = 46 wt% Ni.
Last α to solidify has Cα = 35 wt% Ni.
Cored vs Equilibrium Phases
First α to solidify:
46 wt% Ni
Uniform Cα:
35 wt% Ni
Last α to solidify:
< 35 wt% Ni

19. Chapter 9 - 19
Mechanical Properties: Cu-Ni System
• Effect of solid solution strengthening on:
--Tensile strength (TS)
- Peak as a function of Co
TensileStrength(MPa)
Composition, wt% Ni
Cu Ni
0 20 40 60 80 100
200
300
400
TS for
pure Ni
TS for pure Cu
--Ductility (%EL,%AR)
- Min. as a function of Co
Elongation(%EL) Composition, wt% Ni
Cu Ni
0 20 40 60 80 100
20
30
40
50
60
%EL for
pure Ni
%EL for pure Cu

20. Chapter 9 - 20
Eutectic Phase Diagram
With Eutectic Phase Reaction
L(CE) α(CαE) + β(CβE)
The phase diagram is characterized with:
• 3 single phase regions (L, α and β)
• Partial Solubility – Solubility Limit of
A in B forming β
B in A forming α
Occurs at
L (liquid)
α L + α L+ββ
α + β
Wt% A: Co
1000
T
CE
TE
: Eutectic Composition• CE
• TE : Eutectic Temperature
Remember Phase Reaction at CE
Time
L
L α + β
α + β
T
TE

21. Chapter 9 - 21
Eutectic Phase Diagram – Cooling Curves
L
α L+α L+ββ
α+β
Wt% A: Co
1000
T(°C)
T
Time
L
L α
α
1) Pure A or B
Tmelting
2) Giving α or β
Time
L
L α
α
T
Time
L
L α + β α + β
T
L α
Time
L
L α + β
α + β
T
TE
What is the difference
in this side

22. Chapter 9 - 22
Maximum solubility of A in B
L
α L + α L+ββ
α + β
Wt% A: Co
1000
T(°C)
Liquidus
Solidus
Solvus
Eutectic Reaction
Eutectic Phase Diagram
Maximum solubility of B in A
Boundaries - lines:
•Liquidus
•Solidus
•Solvus
Now, apply previous rules ?
On real systems

23. Chapter 9 - 23

24. Chapter 9 - 24

25. Chapter 9 - 25
Example-Eutectic System
α: mostly Cu
β: mostly Ag
• TE : No liquid below TE
Ex.: Cu-Ag system
L (liquid)
α L + α
L+ββ
α + β
Co , wt% Ag
20 40 60 80 1000
200
1200
T(°C)
400
600
800
1000
CE
TE
8.0%
CE=71.9%
91.2%
TE=779°C
Given T and C Values
are characteristics
Of Cu-Ag system

26. Chapter 9 - 26
L+α
L+β
α + β
200
T(°C)
18.3
C, wt% Sn
20 60 80 1000
300
100
L (liquid)
α 183°C
61.9 97.8
β
• For a 40 wt% Sn-60 wt% Pb alloy at 150°C, find...
--the phases present: Pb-Sn
system
EX: Pb-Sn Eutectic System (1)
α + β
--compositionscompositions of phases:
CO = 40 wt% Sn
--the relative amountrelative amount
of each phase:
150
40
Co
11
Cα
99
Cβ
SR
Cα = 11 wt% Sn
Cβ = 99 wt% Sn
Wα=
Cβ - CO
Cβ - Cα
=
99 - 40
99 - 11
=
59
88
= 0.67
S
R+S
=
Wβ =
CO - Cα
Cβ - Cα
=
R
R+S
=
29
88
= 0.33 (or 1 – 0.67)=
40 - 11
99 - 11

27. Chapter 9 - 27
L+β
α + β
200
T(°C)
C, wt% Sn
20 60 80 1000
300
100
L (liquid)
α β
L+α
183°C
• For a 40 wt% Sn-60 wt% Pb alloy at 200200°°CC, find...
--the phases present: Pb-Sn
system
EX: Pb-Sn Eutectic System (2)
α + L
--compositionscompositions of phases:
CO = 40 wt% Sn
--the relative amountrelative amount
of each phase:
Wα =
CL - CO
CL - Cα
=
46 - 40
46 - 17
=
6
29
= 0.21
WL =
CO - Cα
CL - Cα
=
23
29
= 0.79
40
Co
46
CL
17
Cα
220
SR
Cα = 17 wt% Sn
CL = 46 wt% Sn

28. Chapter 9 - 28
• Co < 2 wt% Sn
• Result:
--at extreme ends
--polycrystal of α grains
i.e., only one solid phase.
Microstructures
in Eutectic Systems: I
0
L+ α
200
T(°C)
Co, wt% Sn
10
2
20
Co
300
100
L
α
30
α+β
400
(room T solubility limit)
TE
(Pb-Sn
System)
α
L
L: Co wt% Sn
α: Co wt% Sn
Depends on the composition

29. Chapter 9 - 29
• 2 wt% Sn < Co < 18.3 wt% Sn
• Result:
 Initially liquid + α
 then α alone
 finally two phases
 α polycrystal
 fine β-phase inclusions
Microstructures
in Eutectic Systems: II
Pb-Sn
system
L + α
200
T(°C)
Co , wt% Sn
10
18.3
200
Co
300
100
L
α
30
α+ β
400
(sol. limit at TE)
TE
2
(sol. limit at Troom)
L
α
L: Co wt% Sn
α
β
α: Co wt% Sn

30. Chapter 9 - 30
• Co = CE
• Result: Eutectic microstructure (lamellar structure)
--alternating layers (lamellae) of α and β crystals.
Microstructures
in Eutectic Systems: III
160µm
Micrograph of Pb-Sn
eutectic
microstructure
Pb-Sn
system
L+β
α + β
200
T(°C)
C, wt% Sn
20 60 80 1000
300
100
L
α β
L+α
183°C
40
TE
18.3
α: 18.3 wt%Sn
97.8
β: 97.8 wt% Sn
CE
61.9
L: Co wt% Sn

31. Chapter 9 - 31
Lamellar Eutectic Structure

32. Chapter 9 - 32
• 18.3 wt% Sn < Co < 61.9 wt% Sn
• Result: α crystals and a eutectic microstructure
Microstructures
in Eutectic Systems: IV
18.3 61.9
SR
97.8
SR
primary α
eutectic α
eutectic β
Pb-Sn
system
L+β200
T(°C)
Co, wt% Sn
20 60 80 1000
300
100
L
α β
L+α
40
α+β
TE
L: Co wt% Sn Lα
L
α

33. Chapter 9 - 33
• 18.3 wt% Sn < Co < 61.9 wt% Sn
• Result: α crystals and a eutectic microstructure
Microstructures
in Eutectic Systems: IV
18.3 61.9
SR
97.8
SR
primary α
eutectic α
eutectic β
WL = (1-Wα) = 0.50
Cα = 18.3 wt% Sn
CL = 61.9 wt% Sn
S
R + S
Wα‘ = = 0.50
• Just above TE :
• Just below TE :
Cα = 18.3 wt% Sn
Cβ = 97.8 wt% Sn
S
R + S
Wα= = 0.73
Wβ = 0.27
Pb-Sn
system
L+β200
T(°C)
Co, wt% Sn
20 60 80 1000
300
100
L
α β
L+α
40
α+β
TE
L: Co wt% Sn Lα
L
α
What is the fraction of
Eutectic α ?
Pro-eutectic (primary) α ?

34. Chapter 9 - 34
L+α
L+β
α + β
200
Co, wt% Sn20 60 80 1000
300
100
L
α β
TE
40
(Pb-Sn
System)
Hypoeutectic & Hypereutectic
160 µm
eutectic micro-constituent
hypereutectic: (illustration only)
β
β
β
β
β
β
175 µm
α
α
α
α
α
α
hypoeutectic: Co = 50 wt% Sn
T(°C)
61.9
eutectic
eutectic: Co =61.9wt% Sn

35. Chapter 9 - 35
Intermetallic Compounds
Note: intermetallic compound forms a line - not an area like α ?
Mg2Pb
In Previous Phase diagrams
α and β are terminal solid
solutions
Can we obtain
other intermediate phases ?
Now: Mg2Pb
• is an intermetallic compound
• with a ratio (2:1) (Mg:Pb)-Molar
• melts at a fixed temperature M
• Cooling curve ???
Because stoichiometry (i.e. composition) is exact: Calculate ?
Calculate Wt% Pb = 207 /(207+2(24.3)) X 100 = 81 %

36. Chapter 9 - 36
Same Story ?
• No. and type of each phase
• Composition of each phase
• Relative amount or fraction of each phase
• Distinguish between
– primary phase
– Eutectic phase
• Microstructure
• Cooling Curves
• Fill the regions with types of phases?

37. Chapter 9 - 37
Eutectoid & Peritectic Phase Reactions
• Eutectic - liquid in equilibrium with two solids
L α + βcool
heat
intermetallic compound
- cementite
cool
heat
• Eutectoid - solid phase in equilibrium with two solid
phases
S2 S1+S3
γ α + Fe3C (727ºC)
cool
heat
• Peritectic - liquid + solid 1  solid 2 (Fig 9.21)
S1 + L S2
δ + L γ (1493ºC)

38. Chapter 9 - 38
Complex Phase Diagrams
α and η are terminal solid solutions - β, β’, γ, δ and ε are intermediate solid solutions.
• new phenomena exist: ……… reaction ………. reaction

39. Chapter 9 - 39
Eutectoid & Peritectic
Cu-Zn Phase diagram
Eutectoid transition δ γ + ε
Peritectic transition γ + L δ

40. Chapter 9 - 40
Phase Diagram with Eutectoid Phase Reactions
The eutectoid (eutectic-like in Greek) reaction is similar to the eutectic
This phase diagram includes both:
Eutectic ReactionEutectoid Reaction
Our Interest In
Fe-C phase diagram

41. Chapter 9 - 41
Iron-Carbon (Fe-C) Phase Diagram
• 2 important points
-Eutectoid (B):
γ ⇒ α +Fe3C
-Eutectic (A):
L ⇒ γ +Fe3C
Fe3C(cementite)
1600
1400
1200
1000
800
600
400
0 1 2 3 4 5 6 6.7
L
γ
(austeniteaustenite)
γ+L
γ+Fe3C
α+Fe3C
α+γ
L+Fe3C
δ
(Fe) Co, wt% C
1148°C
T(°C)
α 727°C = Teutectoid
A
SR
4.30
Result: Pearlite =
alternating layers of
α and Fe3C phases
120 µm
γ γ
γγ
R S
0.76
CeutectoidB
Fe3C (cementite-hardhard)
α(ferriteferrite-softsoft)

42. Chapter 9 - 42
Development of Microstructure in Iron-Carbon alloys
PearlitePearlite Structure
By DiffusionDiffusion
Note: remember the names! Austenite, ferriteferrite, cemetitecemetite and pearlitepearlite

43. Chapter 9 - 43
Hypoeutectoid Steel
Fe3C(cementite)
1600
1400
1200
1000
800
600
400
0 1 2 3 4 5 6 6.7
L
γ
(austenite)
γ+L
γ + Fe3C
α+ Fe3C
L+Fe3C
δ
(Fe) Co, wt% C
1148°C
T(°C)
α
727°C
(Fe-C
System)
C0
0.76
proeutectoid ferritepearlite
100 µm HypoeutectoidHypoeutectoid
steel
R S
α
wα =S/(R+S)
wFe3C =(1-wα)
wpearlite = wγ
pearlite
r s
wα =s/(r+s)
wγ =(1- wα)
γ
γ γ
γα
α
α
γγ
γ γ
γ γ
γγ

44. Chapter 9 - 44
Hypereutectoid Steel
Fe3C(cementite)
1600
1400
1200
1000
800
600
400
0 1 2 3 4 5 6 6.7
L
γ
(austenite)
γ+L
γ +Fe3C
α +Fe3C
L+Fe3C
δ
(Fe) Co, wt%C
1148°C
T(°C)
α
(Fe-C
System)
0.76
Co
proeutectoid FeFe33CC
60 µmHypereutectoid
steel
pearlitepearlite
R S
wα =S/(R+S)
wFe3C =(1-wα)
wpearlite = wγ
pearlite
sr
wFe3C =r/(r+s)
wγ =(1-w Fe3C )
Fe3C
γγ
γ γ
γγ
γ γ
γγ
γ γ

45. Chapter 9 - 45
Phases in Fe–Fe3C Phase Diagram
α -ferrite - solid solution of C in …….. Fe
• Stable form of iron at room temperature.
• The maximum solubility of C is 0.022 wt% (interstitial solubility)
• Soft and relatively easy to deform
+ Fe-C liquid solution
γ -austenite - solid solution of C in …….. Fe
The maximum solubility of C is 2.14 wt % at 1147°C.
Interstitial lattice positions are much larger than ferrite (higher C%)
Is not stable below the eutectic temperature (727 °C) unless cooled rapidly
(Chapter 10).
δ -ferrite solid solution of C in ……. Fe
The same structure as α -ferrite
Stable only at high T, above 1394 °C
Also has low solubility for carbon (BCC)
Fe3C (iron carbide or cementite)
This intermetallic compound is metastable,
it remains as a compound indefinitely at room T,
but decomposes (very slowly, within several years) into α -Fe and C
(graphite) at 650 - 700 °C

46. Chapter 9 - 46
Example: Phase Equilibria
For a 99.6 wt% Fe-0.40 wt% C at a temperature
just below the eutectoid, determine the
following
a) composition of Fe3C and ferrite (α)
b) the amount of carbide (cementite) in grams
that forms per 100 g of steel
c) the amount of pearlite and proeutectoid
ferrite (α)

47. Chapter 9 - 47
Example – Fe-C System
g3.94
g5.7CFe
g7.5100
022.07.6
022.04.0
100x
CFe
CFe
3
CFe3
3
3
=α
=
=
−
−
=
−
−
=
α+ α
α
x
CC
CCo
b) the amount of cementite in grams
that forms per 100 g of steel
a) composition of Fe3C and ferrite (α)
CO = 0.40 wt% C
Cα = 0.022 wt% C
CFe C = 6.70 wt% C
3
FeC(cementite)
1600
1400
1200
1000
800
600
400
0 1 2 3 4 5 6 6.7
L
γ
(austenite)
γ+L
γ + Fe3C
α + Fe3C
L+Fe3C
δ
Co, wt% C
1148°C
T(°C)
727°C
CO
R S
CFe C3Cα

48. Chapter 9 - 48
Chapter 9 – Phase Equilibria
c. the amount of pearlite and proeutectoid ferrite (α)
note: amount of pearlitepearlite = amount of γγ just abovejust above TE
Co = 0.40 wt% C
Cα = 0.022 wt% C
Cpearlite = Cγ = 0.76 wt% C
γ
γ+α
=
Co −Cα
Cγ−Cα
x 100 =51.2 g
pearlite = 51.2 g
proeutectoid α = 48.8 g
FeC(cementite)
1600
1400
1200
1000
800
600
400
0 1 2 3 4 5 6 6.7
L
γ
(austenite)
γ+L
γ + Fe3C
α + Fe3C
L+Fe3C
δ
Co, wt% C
1148°C
T(°C)
727°C
CO
R S
CγCα
Pearlite include ?
Eutectoid Fe3CFe3C
+
Eutectoid ferriteferrite αα

49. Chapter 9 - 49
Alloying Steel with More Elements
• Teutectoid changes: • Ceutectoid changes:
TEutectoid(°C)
wt. % of alloying elements
Ti
Ni
Mo
Si
W
Cr
Mn
wt. % of alloying elements
Ceutectoid(wt%C)
Ni
Ti
Cr
Si
Mn
W
Mo

50. Chapter 9 - 50
• Phase diagrams are useful tools to determine:
--the number and types of phases,
--the wt% of each phase,
--and the composition of each phase
for a given T and composition of the system.
• Alloying to produce a solid solution usually
--increases the tensile strength (TS)
--decreases the ductility.
• Binary eutectics and binary eutectoids allow for
a range of microstructures.
Summary