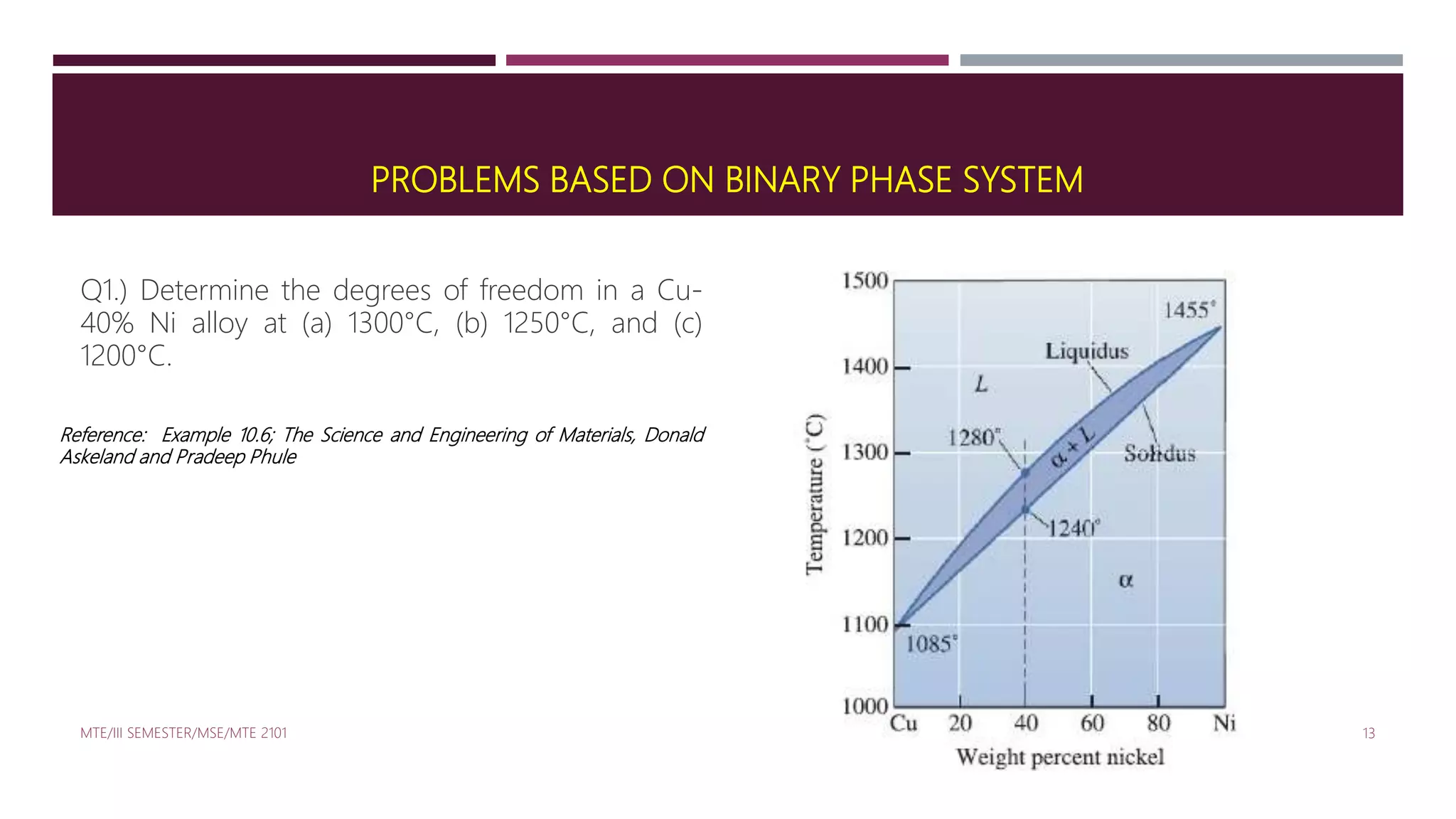
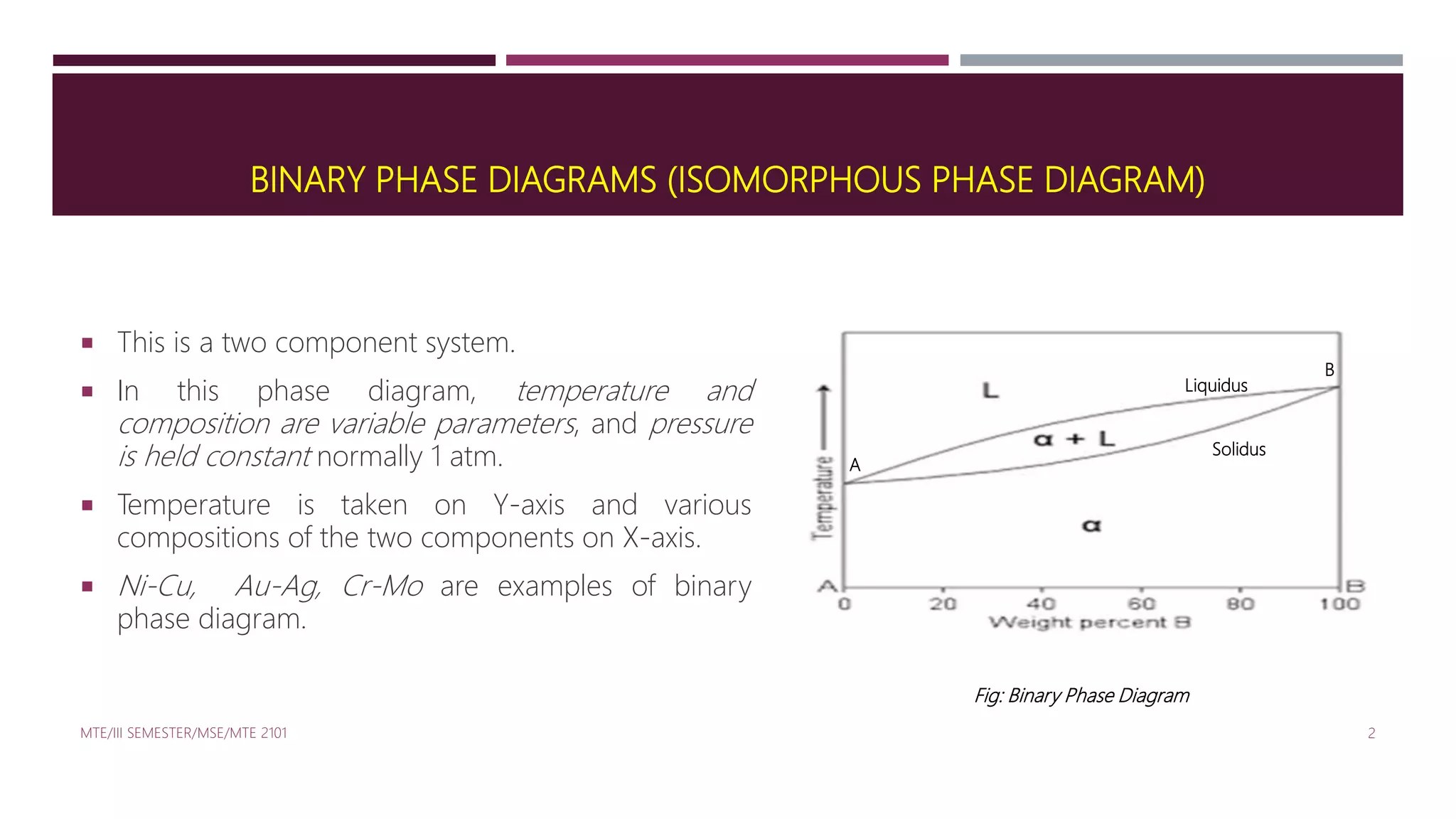
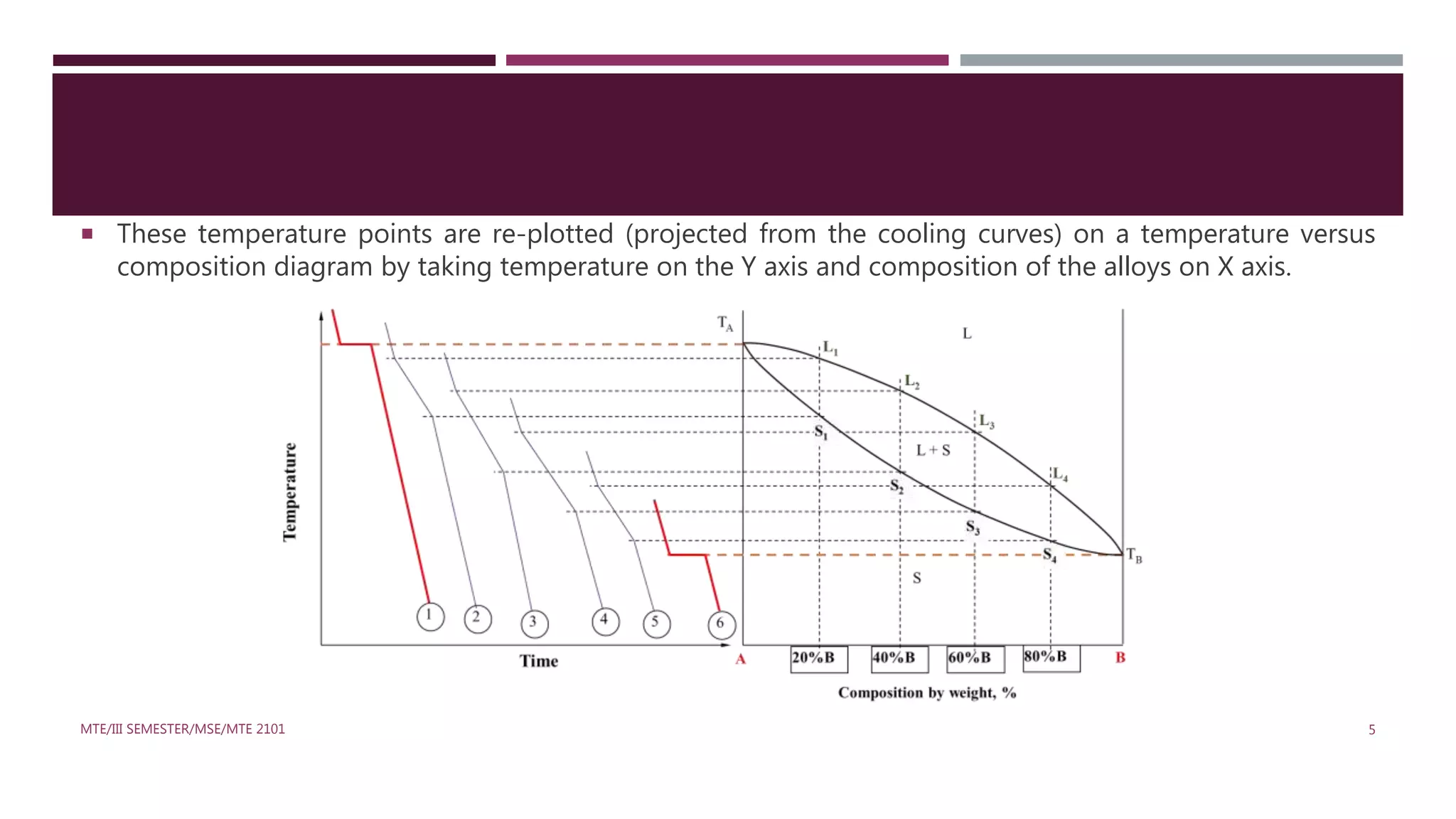
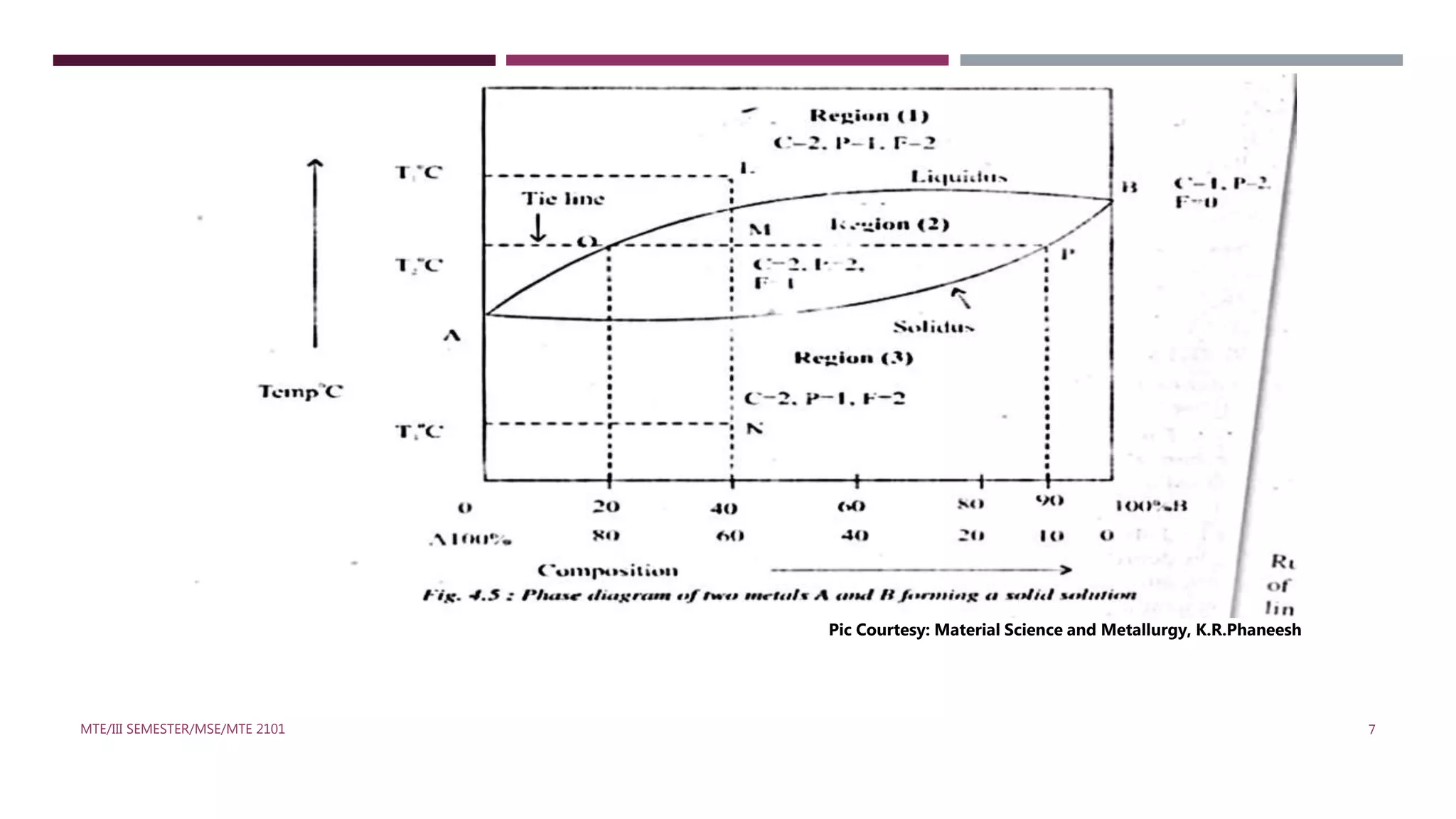
This document discusses binary phase diagrams in materials science, focusing on their description, construction, and interpretation. It explains key concepts such as liquidus and solidus curves, Gibb's phase rule, tie-lines, and lever rules for determining phase compositions and amounts. Problems related to binary phase systems, particularly involving Cu-Ni alloys, are also presented for practical understanding.

1. CHAPTER 2 (CONTD.)
 Binary Phase System
1. Description of Binary Phase Diagram
2. Construction of Binary Phase Diagram
3. Interpretation of Binary Phase Diagram
i. Modified Gibb’s Phase Rule
ii. Tie-Line
iii. Lever Rule
4. Problems based on Binary Phase Diagram
MTE/III SEMESTER/MSE/MTE 2101 1

2. BINARY PHASE DIAGRAMS (ISOMORPHOUS PHASE DIAGRAM)
 This is a two component system.
 In this phase diagram, temperature and
composition are variable parameters, and pressure
is held constant normally 1 atm.
 Temperature is taken on Y-axis and various
compositions of the two components on X-axis.
 Ni-Cu, Au-Ag, Cr-Mo are examples of binary
phase diagram.
MTE/III SEMESTER/MSE/MTE 2101 2
Fig: Binary Phase Diagram
Liquidus
Solidus
A
B

3. Description of Binary Phase Diagram
 For all combinations of temperature and composition
above liquidus curve (AB), the mixture is in the liquid
state.
 Liquidus temperature as the temperature above which a
material is completely liquid.
 The solidus temperature is the temperature below which
the alloy is 100% solid.
 For all combinations of temperature and composition
below solidus curve (BA), the mixture is in the solid state.
state.
 Point A and B represent the melting temperatures of
individual alloy.
 The temperature difference between the liquidus and the
solidus is the freezing range of the alloy.MTE/III SEMESTER/MSE/MTE 2101 3
Liquidus
Solidus
A
B
Fig: Binary Phase Diagram

4. Construction of Binary Phase Diagram
 Phase diagrams for a binary alloy system can be obtained from
cooling curves of the system at various compositions of the two
components.
 Let us consider two metals A and B.
 Curve A and B represent the cooling curve of pure metal A and
 Curve U,V,W,X represent cooling curves of alloy of A and B at
different compositions.
NOTE: Phase diagram show the relationship of phases at equilibrium
conditions. This means the phases present at particular temperature
and composition don't change with time.
MTE/III SEMESTER/MSE/MTE 2101 4
U
V
W
X
Fig: Cooling curves of metal A and B, alloy mixture of A
and B

5.  These temperature points are re-plotted (projected from the cooling curves) on a temperature versus
composition diagram by taking temperature on the Y axis and composition of the alloys on X axis.
MTE/III SEMESTER/MSE/MTE 2101 5

6. Interpretation of Binary Phase Diagram – Using Phase Rule, Tie-Line and Lever Rule
 For a binary system of known composition and temperature that is at equilibrium, at least three kinds
information are available: (1) the phases that are present, (2) the compositions of these phases, and (3)
the percentages or fractions of the phases.
 For determining the degrees of freedom in a binary phase diagram, Modified Gibb’s Phase Rule ( P+F
= C+1) is used. (Pressure is assumed to be 1 atm)
 To determine the phase composition present at any point, Tie Line is used.
 To determine the amount of each phase present at any point, Lever Rule is used.
MTE/III SEMESTER/MSE/MTE 2101 6

7. MTE/III SEMESTER/MSE/MTE 2101 7
Pic Courtesy: Material Science and Metallurgy, K.R.Phaneesh

8. Modified Gibb’s Phase Rule:
 Points A and B represent the melting temperatures of A and B. The degrees of freedom, F = 0 at these
points because number of phases, P=2, Number of components, C=1.
 These points are called as “Invariant Points”.
Region 1:
 Single phase homogeneous region.
 Number of Components, C =2 (i.e. Liq.A and Liq.B)
 Number of Phases, P = 1 (i.e. Liquid Phase)
Applying Modified Gibb’s Phase Rule(P+F = C+1):
 Number of Degrees of Freedom, F = 2
MTE/III SEMESTER/MSE/MTE 2101 8

9. Region 2:
 Mixture of solid and liquid phase.
 Number of Components, C = 2. (i.e. Liq + α)
 Number of Phases, P = 2. (i.e. Liquid and Solid)
Applying Modified Gibb’s Phase Rule(P+F = C+1):
 Number of Degrees of Freedom, F = 1
Region 3:
 Single phase solid region.
 Similar to region 1.
MTE/III SEMESTER/MSE/MTE 2101 9

10.  Let us consider an alloy consisting of 60% A and 40% B.
 At point L, the mixture is a single phase homogeneous liquid at T₁°C.
 At point N, the mixture is fully in solid state at T₃°C.
 At point M, where solidification is in progress, there is a two phase mixture of solid and liquid, both of
metals A and B.
 Two questions arise: 1. What are solid and liquid composition?
2. What are the amounts of solid and liquid phase?
MTE/III SEMESTER/MSE/MTE 2101 10

11. Phase Composition (Tie - Line):
 At point M, a horizontal “tie line” or “constant temperature line” is drawn which intersects the liquidus
MTE/III SEMESTER/MSE/MTE 2101 11

12. Amount of each phase present (Lever Rule):
 Lever Rule states that,” The relative amount of each phase is directly proportional to the length of
opposite lever arm”.
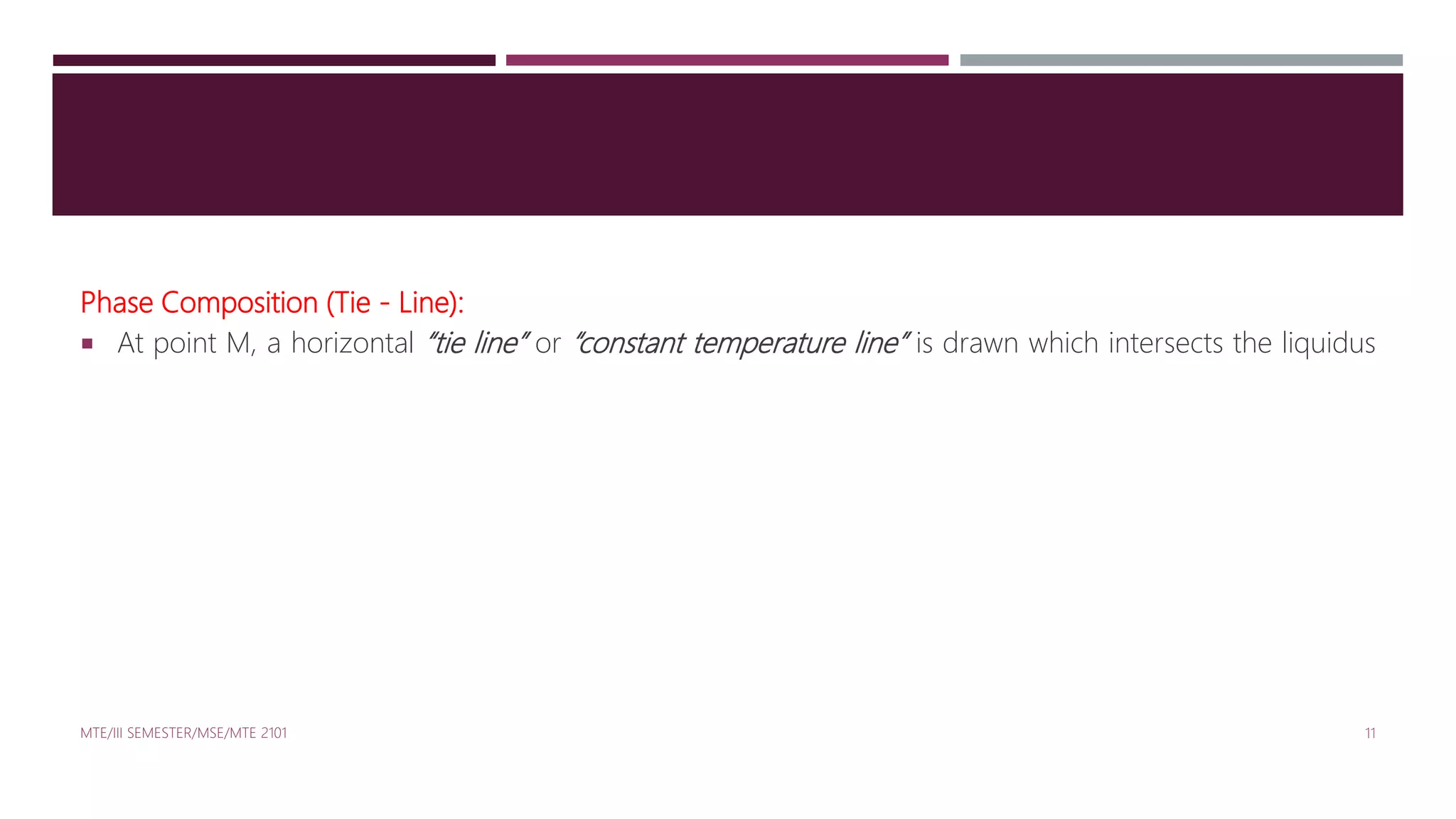
 The tie-line OMP has two arms OM and MP which intersects the liquidus and solidus curves.
 According to Lever Rule, the length MP touching the solidus proportional to the amount of liquid
present at M and the length OM touching the liquidus is proportional to the amount of solid phase
present at M.
Therefore,
Amount of liquid phase at M =
𝑴𝑷
𝑶𝑷
× 100 =
[𝟗𝟎−𝟒𝟎]
[𝟗𝟎−𝟐𝟎]
× 100 = 71.42% .
Amount of solid phase at M =
𝑶𝑴
𝑶𝑷
× 100 =
[𝟒𝟎−𝟐𝟎]
[𝟗𝟎−𝟐𝟎]
× 100 = 28.58% .
MTE/III SEMESTER/MSE/MTE 2101 12

13. PROBLEMS BASED ON BINARY PHASE SYSTEM
Q1.) Determine the degrees of freedom in a Cu-
40% Ni alloy at (a) 1300°C, (b) 1250°C, and (c)
1200°C.
MTE/III SEMESTER/MSE/MTE 2101 13
Reference: Example 10.6; The Science and Engineering of Materials, Donald
Askeland and Pradeep Phule

14. Q2.) Determine the composition of each phase in a Cu-
40% Ni alloy at 1300°C, 1270°C, 1250°C, and 1200°C.
MTE/III SEMESTER/MSE/MTE 2101 14
Reference: Example 10.7; The Science and Engineering of Materials,
Donald Askeland and Pradeep Phule

15. Q3.) Calculate the amounts of and L at 1250°C in the
Cu-40% Ni alloy shown in Figure.
MTE/III SEMESTER/MSE/MTE 2101 15
Reference: Example 10.8; The Science and Engineering of Materials, Donald Askeland and
Pradeep Phule