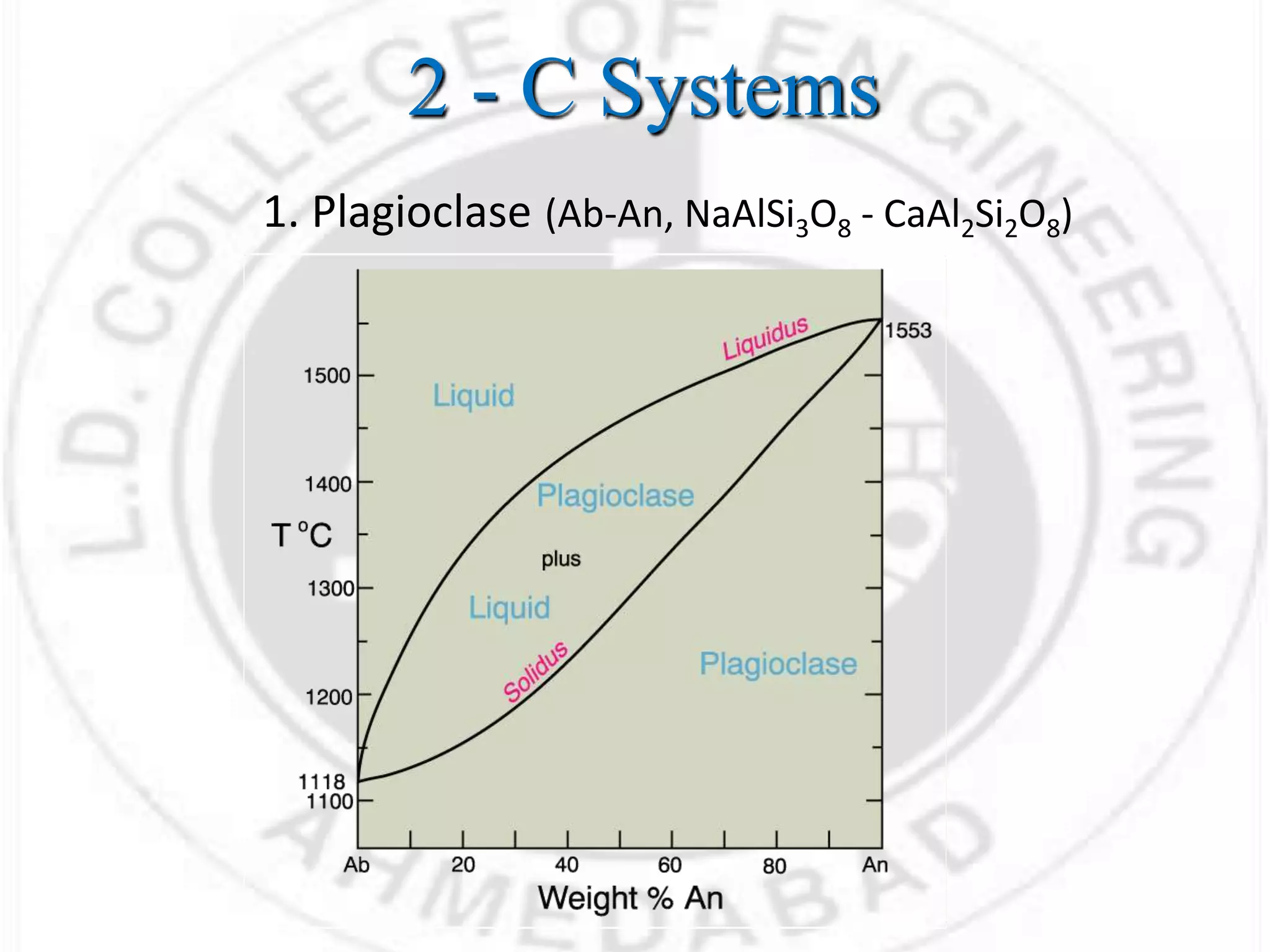
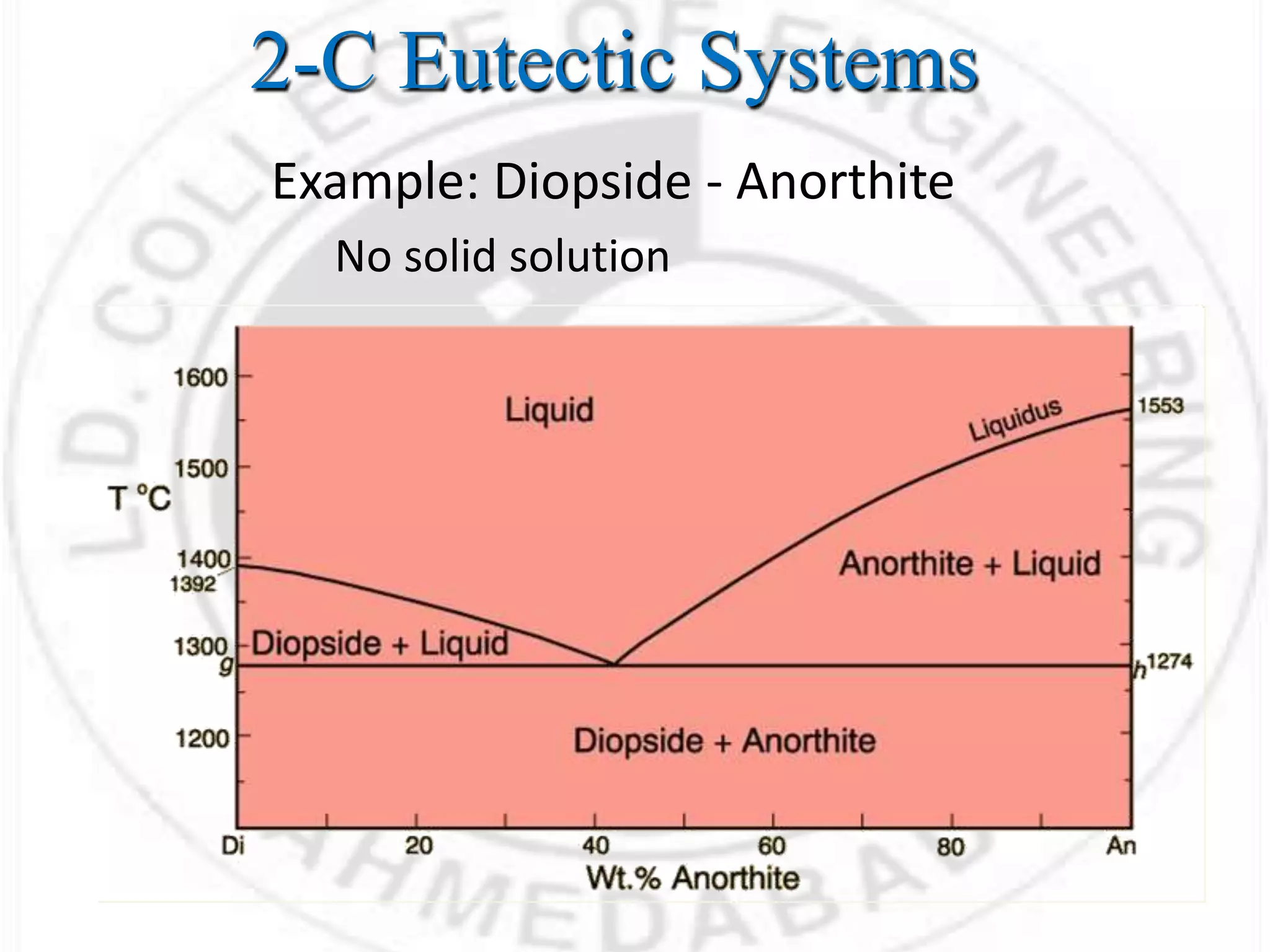
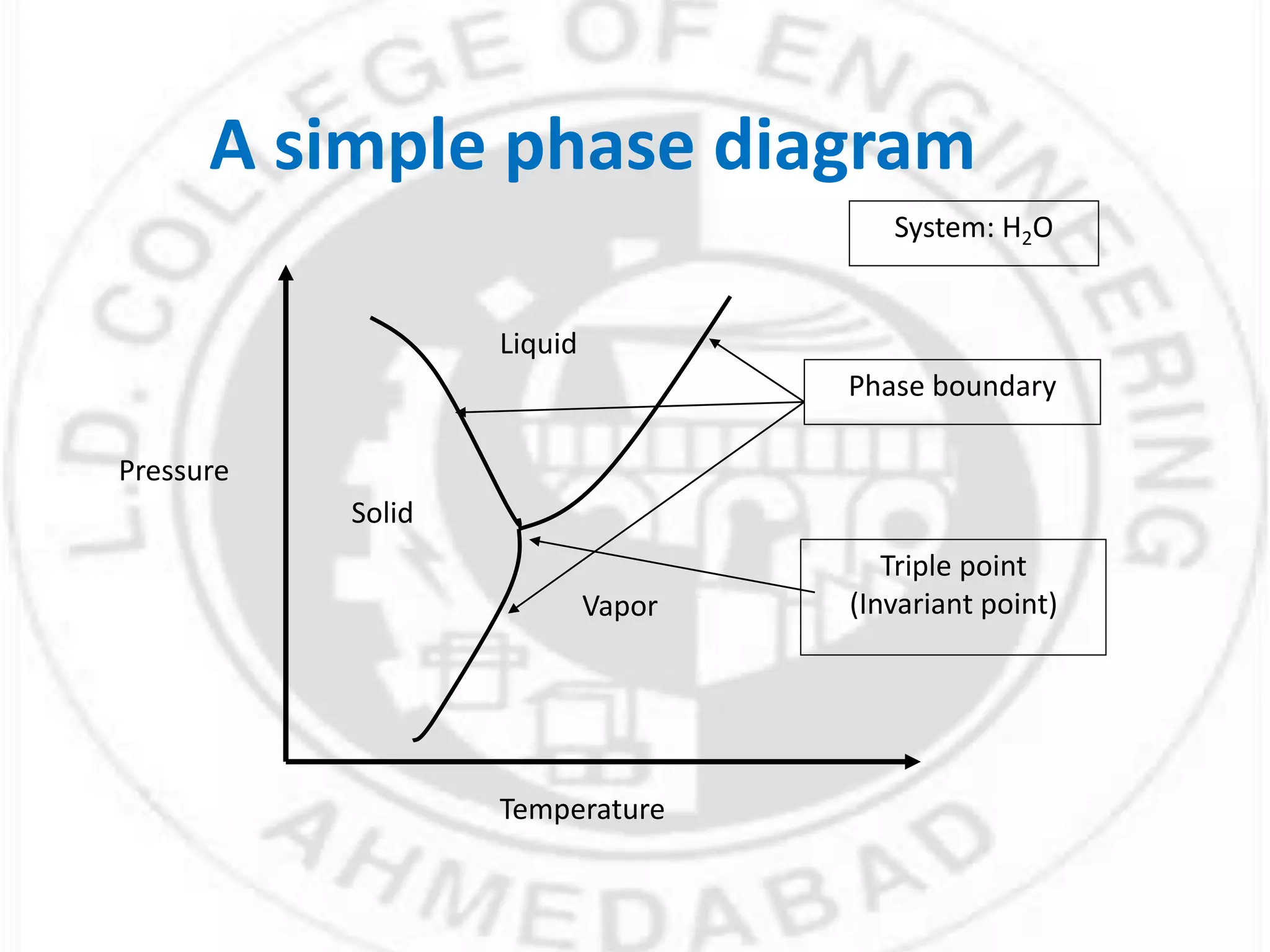
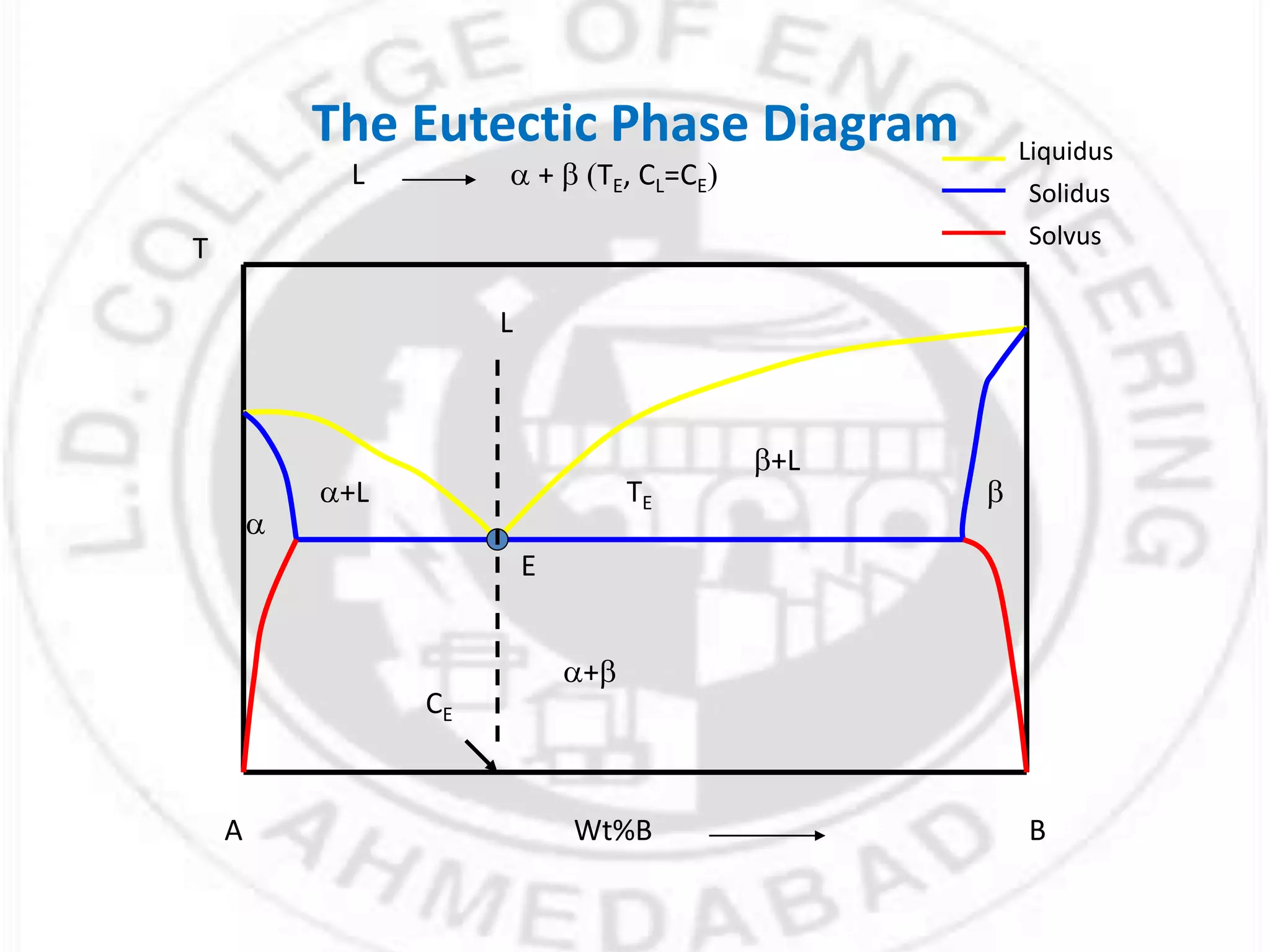
This document discusses basic concepts related to thermodynamics of elastomers and polymers, including: - Phases can be solid, liquid, or gas and exist in homogeneous regions with distinct properties. Phase diagrams show the phases present under different conditions. - Gibbs phase rule relates the number of phases (f), components (C), and degrees of freedom (F) using the equation F = C - f + 2. It describes the number of intensive parameters needed to determine a system at equilibrium. 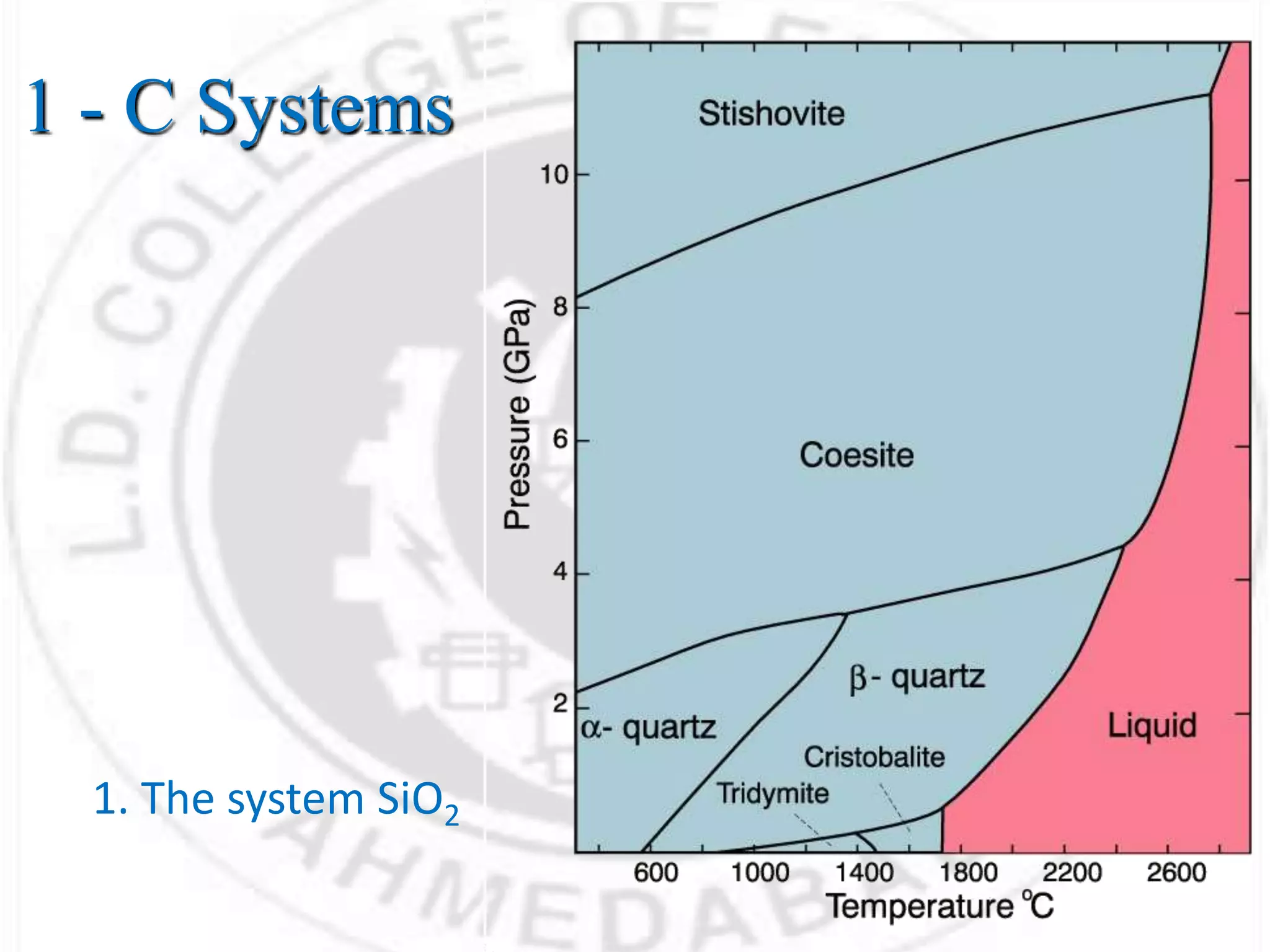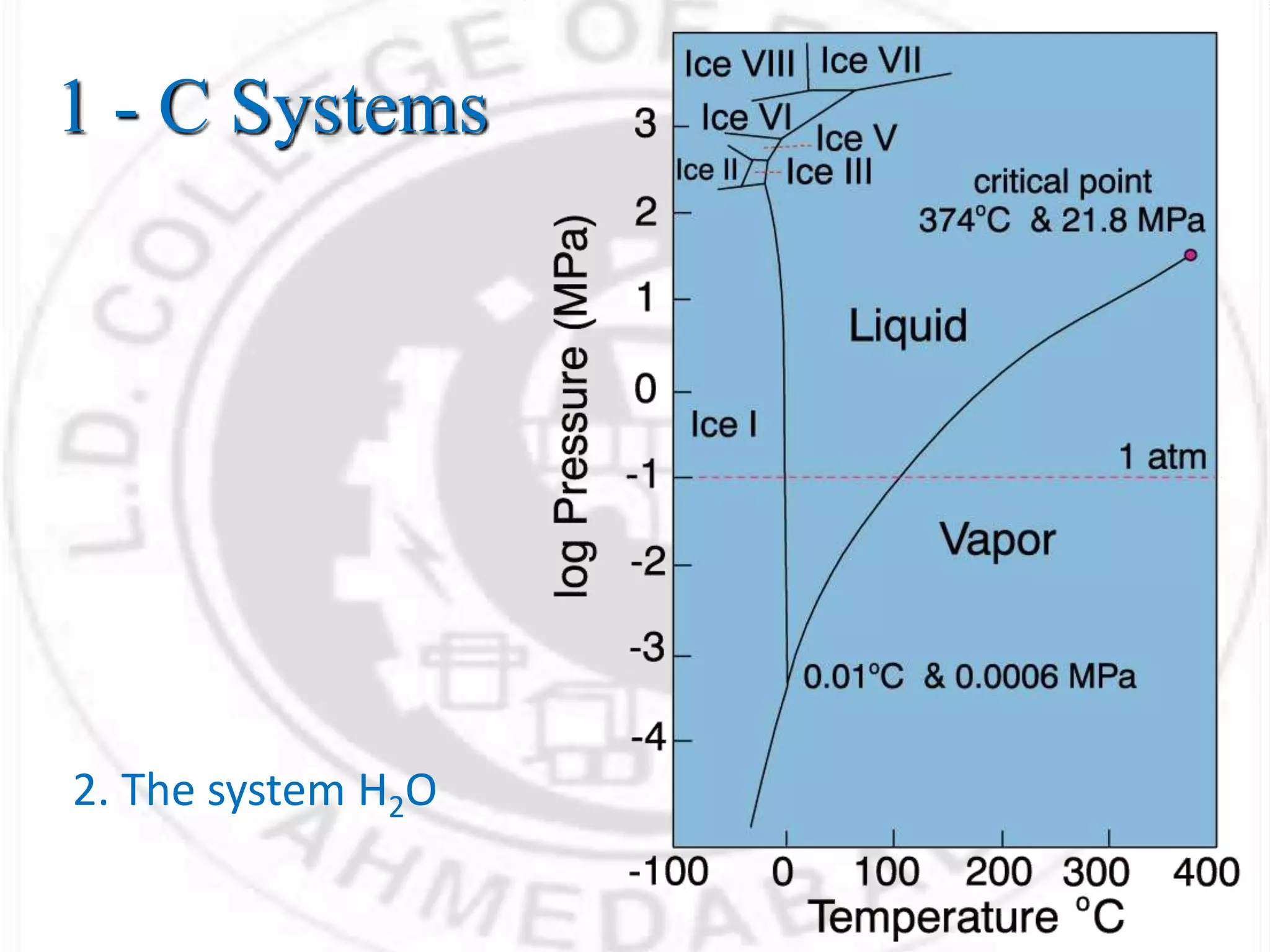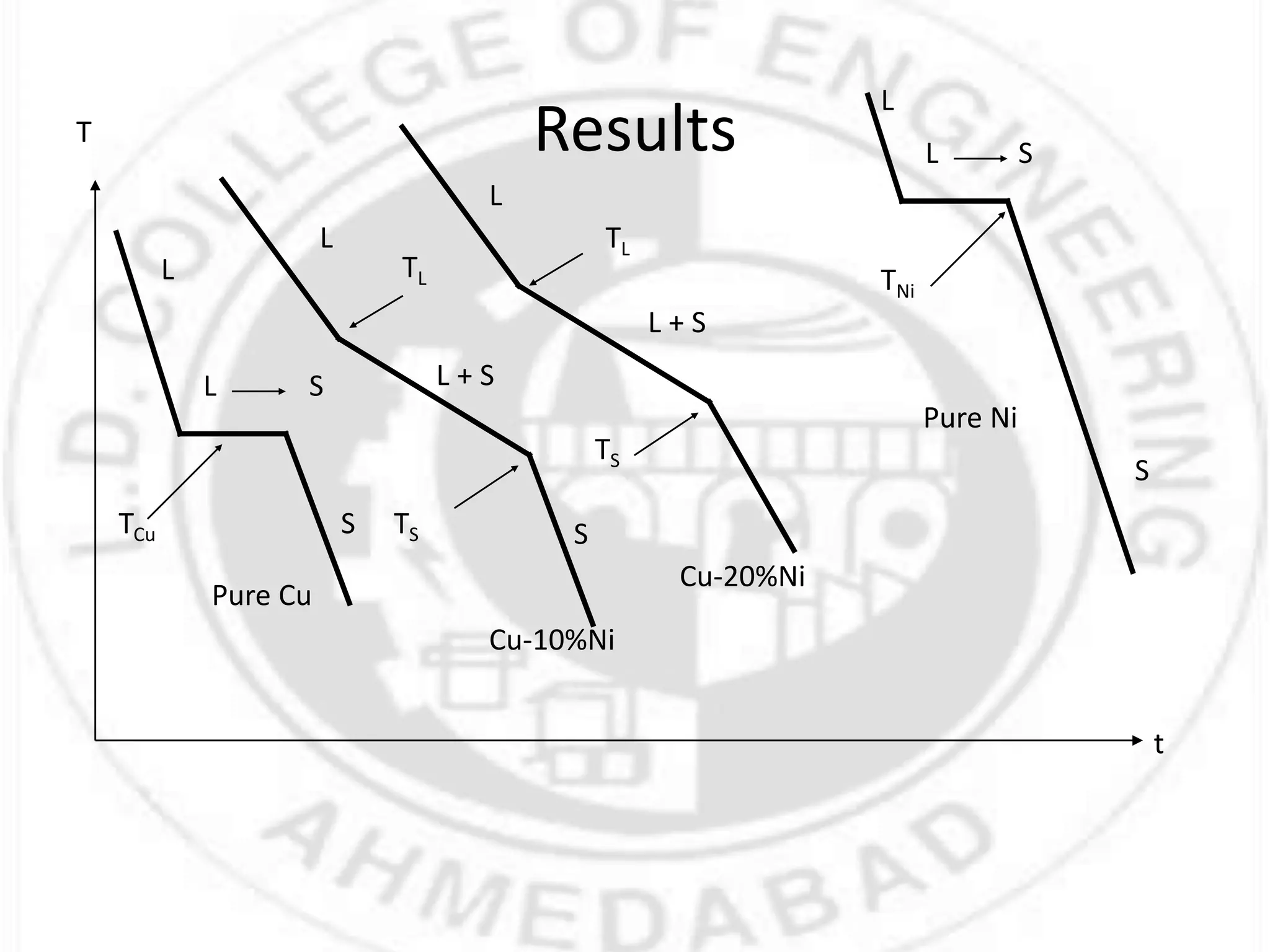- For a single component system like water, equilibrium between the liquid and vapor phases requires only one state variable like temperature according to Gibbs phase rule. Phase diagrams can be constructed by conducting experiments on samples and recording phase

1. L. D. COLLEGE OF
ENGINEERING
RUBBER TECHNOLOGY
Sub:- THERMODYNAMICS OF
ELASTOMERS & POLYMERS

3. Some basic concepts
• Phase
– A homogeneous region with distinct structure
and physical properties
– In principle, can be isolated
– Can be solid, liquid or gas
• Phase Diagram
– Representation of phases present under a set
of conditions (P, T, Composition etc.)

4. F = C - f + 2
F = # degrees of freedom
The number of intensive parameters that must be specified
in order to completely determine the system
f = # of phases
phases are mechanically separable constituents
C = minimum # of components (chemical constituents that must
be specified in order to define all phases)
The Phase Rule

5. Gibbs Phase Rule
For a closed, homogeneous system of constant composition (e.g., an ideal gas), we require two
parameters of state (for example, T and p) in order to describe it. For a heterogeneous system
in equilibrium, consisting of one component (e.g., water substance) and two phases (e.g., liquid
and vapour), we require only one parameter of state (for example, T).
This example may be expressed more generally in terms of Gibb’s phase rule:
v = c -f + 2
where =number of independent state variables at equilibrium
c=number of components
f =number of phases
We assume here that the masses of the components and phases are specified. As an
example,
For equilibrium between a pure plane surface of water and its vapour, we require only one
state

6. Gibb’s Phase Rule
P + F = C + 2 P=number of phases
C=number of components
F=number of degrees of freedom
(number of independent variables)
Modified Gibbs Phase Rule (for incompressible systems)
P + F = C + 1
Pressure is a constant variable
F = C - P + 2
F = C - P + 1

7. Application of the phase rule
At triple point, P=3, C=1, F=0
i.e. this is an invariant point
At phase boundary, P=2, C=1, F=1
In each phase, P=1, C=1, F=2

8. The Phase Rule
There are two types of phase
components as per below;
=> One Component Systems
=> Two Component Systems

9. 1 - C Systems
1. The system SiO2

10. 1 - C Systems
2. The system H2O

11. 2 - C Systems
1. Plagioclase (Ab-An, NaAlSi3O8 - CaAl2Si2O8)

12. 2-C Eutectic Systems
Example: Diopside - Anorthite
No solid solution

13. A simple phase diagram
Triple point
(Invariant point)
Solid
Liquid
Vapor
Pressure
Temperature
Phase boundary
System: H2O

14. Construction of a simple phase diagram
• Conduct an experiment
• Take 10 metal samples(pure Cu, Cu-10%Ni,
Cu-20%Ni, Cu-30%Ni………, pure Ni)
• Melt each sample and then let it solidify
• Record the cooling curves
• Note temperatures at which phase
transformations occur

15. Results
L
S
L S
t
T
L
L + S
TL
TS S
L
L + S
TL
TS
Pure Cu
Cu-10%Ni
Cu-20%Ni
L
L S
Pure Ni
S
TNi
TCu

16. The Eutectic Phase Diagram
T
A BWt%B
L
a+L
b+L
a+b
E
TE
CE
a
b
Liquidus
Solidus
Solvus
L a + b (TE, CL=CE)