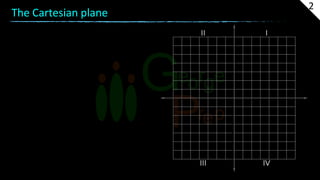
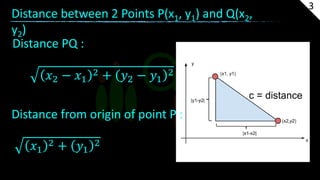
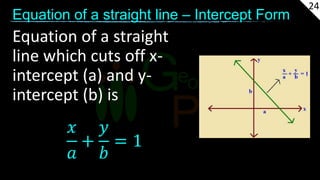
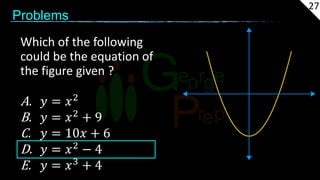
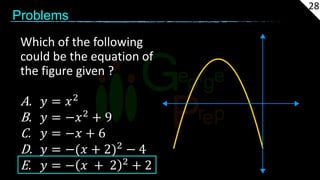
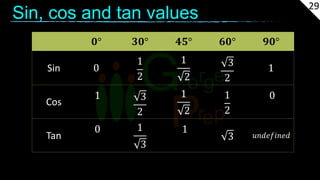
The document provides information about coordinate geometry and straight lines. It defines key concepts like the Cartesian plane, distance between points, slopes of lines, equations of lines in various forms, and transformations of graphs. It also gives examples of determining the type of triangles based on side lengths and slopes, finding equations of lines satisfying given conditions, and identifying collinear points. Practice problems are included at the end to test the understanding of these geometric and algebraic concepts.

1. Coordinate Geometry
Concept Session

2. The Cartesian plane
2

3. Distance between 2 Points P(x1, y1) and Q(x2,
y2)
Distance PQ :
𝑥2 − 𝑥1
2 + 𝑦2 − 𝑦1
2
Distance from origin of point P :
𝑥1
2 + 𝑦1
2
3

4. Distance between 2 Points - Problems
Let the vertices of a triangle ABC be
(−8, 8), (2, −8) and (−2, 2) then the triangle is
A. Right angled
B. Equilateral
C. Isosceles
D. Scalene
E. Cannot be determined
4

5. The midpoint of an interval
The midpoint of an interval with endpoints
𝑃(𝑥1, 𝑦1) and 𝑄(𝑥2, 𝑦2) is
𝑥1 + 𝑥2
2
,
𝑦1 + 𝑦2
2
5

6. The midpoint of an interval - Problem
If C(3, 5) is the midpoint of line interval AB
and A has coordinates (–2, 1), find the
coordinates of B.
6
Answer : (8, 9)

7. Section formula – Internal
division
Given two end points of line segment A(x1, y1) and B
(x2, y2) you can determine the coordinates of the point
P(x, y) that divides the given line segment in the ratio
m : n internally using Section Formula
𝑥 =
𝑚𝑥2+𝑛𝑥1
𝑚+𝑛
𝑦 =
𝑚𝑦2+𝑛𝑦1
𝑚+𝑛
7

8. Section formula – External
division
Given two end points of line segment A(x1, y1) and B
(x2, y2) you can determine the coordinates of the point
P(x, y) that divides the given line segment in the ratio
m : n externally using Section Formula given by
𝑥 =
𝑚𝑥2−𝑛𝑥1
𝑚−𝑛
𝑦 =
𝑚𝑦2−𝑛𝑦1
𝑚−𝑛
8

9. Area of a Triangle
The area of a triangle ABC whose vertices are
A(x1, y1), B (x2, y2) and C(x3, y3) is denoted by
1
2
| 𝑥1 𝑦2 − 𝑥2 𝑦1 + 𝑥2 𝑦3 − 𝑥3 𝑦2
+ 𝑥3 𝑦1 − 𝑥1 𝑦3 |
9

10. Centroid of a triangle
Centroid – meeting point of the three medians.
The centroid(G) of a triangle ABC whose vertices are
A(𝑥1, 𝑦1), B(𝑥2, 𝑦2) and C(𝑥3, 𝑦3) is denoted by
𝐺 =
𝑥1 + 𝑥2 + 𝑥3
3
,
𝑦1 + 𝑦2 + 𝑦3
3
10

11. Straight Line
▪Slope of a Line
▪Equations of a straight line
–General form of Equation
–Slope-intercept form
–Point slope form
–Two point form
–Intercept form
11

12. Slope of a line ( Gradient)
The slope, represented by the letter m, measures
the inclination or steepness of the line.
The slope is always measured anti-clock wise
𝑆𝑙𝑜𝑝𝑒 =
𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑦 𝑐𝑜𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒
𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑥 𝑐𝑜𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒
=
𝑅𝑖𝑠𝑒
𝑅𝑢𝑛
𝑆𝑙𝑜𝑝𝑒 =
∆𝑦
∆𝑥
=
𝑦2 − 𝑦1
𝑥2 − 𝑥1
12

13. Slope of a line ( Gradient) - values
Positive Slope – On moving from
left to right, the line rises
Negative Slope - On moving from left
to right, the line dips
13

14. Slope of a line ( Gradient) - values
Zero Slope – Parallel to x axis and
hence “No rise”
Undefined Slope – Parallel to y axis
and hence “ infinite rise”
14

15. Slope of a special line
Parallel Lines  equal slope
𝑚1 = 𝑚2
Perpendicular lines  negative
inverses
𝑚1 ∗ 𝑚2 = −1
15

16. Problems
16
Quantity A Quantity B
Sole of a line
perpendicular to
Line 1
Slope of a line
perpendicular to
Line 2

17. Equation of a straight line – General Form
𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0
Slope of the line =
−𝑎
𝑏
Y intercept =
𝑐
𝑏
17

18. Equation of a straight line – Slope intercept Form
Equation of a straight line whose slope
is 𝑚 and which cuts of a y-intercept of 𝐶
units is given by
𝑦 = 𝑚𝑥 + 𝐶
18

19. Equation of a straight line – Problems
Find the equation of a line that
intersects the Y axis at the point
(0,3) and has a slope of
5
3
Answer : 3𝑦 − 5𝑥 = 9
19

20. Equation of a straight line – Point-slope Form
Equation of a straight line passing
through a point (𝑥1, 𝑦1) and having a
slope m is given by
𝑦 − 𝑦1 = 𝑚 ∗ (𝑥 − 𝑥1)
20

21. Equation of a straight line – Problems
Find an equation of the line that passes through
(4, 6) and is parallel to the line whose equation is
𝑦 =
2
3
𝑥 + 5.
a) 2𝑦 = 3𝑥 + 10
b) 3𝑦 = 3𝑥 + 10
c) 3𝑦 = 2𝑥 + 10
d) 4𝑦 = 3𝑥 + 15
e) 𝑛𝑜𝑛𝑒 𝑜𝑓 𝑡ℎ𝑒𝑠𝑒
Answer: Option
3
21

22. Equation of a straight line – Problems
Find an equation of the line that passes through
(4, 6) and is perpendicular to the line whose
equation is 𝑦 =
2
3
𝑥 + 5.
1. 2𝑦 = −3𝑥 + 10
2. 3𝑦 = −3𝑥 + 24
3. 3𝑦 = 2𝑥 + 10
4. 4𝑦 = 3𝑥 + 13
5. 𝑛𝑜𝑛𝑒 𝑜𝑓 𝑡ℎ𝑒𝑠𝑒
Answer: 2𝑦 = −3𝑥 + 24
22

23. Equation of a straight line – Two-point Form
Equation of a straight line passing
through two points (𝑥1, 𝑦1) and (𝑥2, 𝑦2)
is given by
𝑦 − 𝑦1 =
(𝑦2−𝑦1)
(𝑥2−𝑥1)
∗ (𝑥 − 𝑥1)
23

24. Equation of a straight line – Intercept Form
Equation of a straight
line which cuts off x-
intercept (a) and y-
intercept (b) is
𝑥
𝑎
+
𝑦
𝑏
= 1
24

25. Transformations – Vertical and Horizontal Shifts
25
Vertical Shift
To Graph Shift the Graph of ƒ(x)
ƒ(𝑥) + 𝑐 c units upward
ƒ 𝑥 − 𝑐 c units upward
Horizontal Shift
To Graph Shift the Graph of ƒ(x)
ƒ(𝑥 + 𝑐) c units to the left
ƒ 𝑥 − 𝑐 c units to the right

26. Transformations – Reflections
26
Reflection along coordinate axis
To Graph Shift the Graph of ƒ(x)
−ƒ(𝑥) Reflect along x axis
ƒ −𝑥 Reflect along y axis

27. Problems
27
Which of the following
could be the equation of
the figure given ?
A. 𝑦 = 𝑥2
B. 𝑦 = 𝑥2
+ 9
C. 𝑦 = 10𝑥 + 6
D. 𝑦 = 𝑥2
− 4
E. 𝑦 = 𝑥3
+ 4

28. Problems
28
Which of the following
could be the equation of
the figure given ?
A. 𝑦 = 𝑥2
B. 𝑦 = −𝑥2
+ 9
C. 𝑦 = −𝑥 + 6
D. 𝑦 = −(𝑥 + 2)2
− 4
E. 𝑦 = − 𝑥 + 2 2
+ 2

29. Sin, cos and tan values
𝟎° 𝟑𝟎° 𝟒𝟓° 𝟔𝟎° 𝟗𝟎°
Sin 0
1
2
1
2
3
2
1
Cos
1 3
2
1
2
1
2
0
Tan
0 1
3
1
3 𝑢𝑛𝑑𝑒𝑓𝑖𝑛𝑒𝑑
29

30. Conditions of Collinearity of three Points
1. Area of triangle ABC is zero.
2. Slope of AB = Slope of BC = Slope of AC
3. Distance between A and B + Distance between
B and C = Distance between A and C
30

31. Practice Problems
If 𝐴(1,2), 𝐵(4,3), 𝐶(6,6) and 𝐷(𝑥, 𝑦) are the
four vertices of a parallelogram taken in an
order, then the value of 𝑥 + 𝑦 is
A. 5
B. 7
C. 8
D. 10
E. None of these
Answer : option 3
31