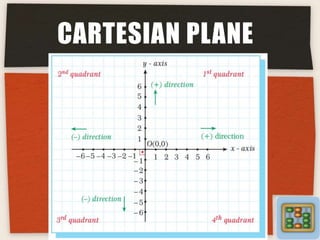
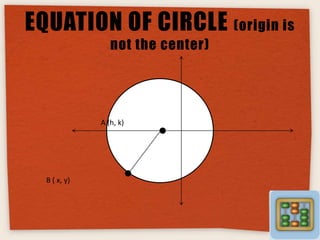
This document provides an overview of analytical geometry. It discusses how analytical geometry was introduced in the 1630s and aided the development of calculus. Rene Descartes and Pierre de Fermat independently developed the foundations of analytical geometry. It describes the Cartesian plane and key concepts like the x-axis, y-axis, origin, coordinates, slope of a line, angle between lines, slope of parallel and perpendicular lines, and the equation of a circle. Sample problems and references are also included.

1. ANALYTICAL
GEOMETRY
SJ van Heerden
09/03/2014

2. HISTORY
Introduced in the 1630s
Aided the development of calculus
RENE DESCARTES (1596-1650) and
PIERRE DE FERMAT (1601-1665),
French mathematicians,
independently developed
the foundations for
analytical geometry

3. CARTESIAN PLANE

4. • x-axis (horizontal axis) where the x values are
plotted along.
• y-axis (vertical axis) where the y values are
plotted along.
• origin, symbolized by 0, marks the value of 0 of
both axes
• coordinates are given in the form (x,y) and is
used to represent different points on the plane.

11. Slope of a Line

14. Slope of a Line

15. Slope of a Line

16. Slope of a Line

17. Slope of a Line

18. Inclination of a Line
y
y
L
L
θ
O
M
x
θ
O
M
x

20. Angle between Two
Lines

21. Angle between Two
Lines
• If θ is angle, measured counter-clockwise,
between two lines, then
• where m2 is the slope of the terminal side and
m1 is the slope of the initial side

24. SLOPE OF PARALLEL LINES

26. SLOPE OF PERPENDICULAR LINES

48. Sample Problems

54. EQUATION OF A CIRCLE

57. EQUATION OF CIRCLE (origin is
not the center)
A (h, k)
B ( x, y)

59. Graph the following circle.

60. REFERENCES
- Demirdag, M. (2013). Analytic geometry [PowerPoint Presentation]. Available at:
http://www.slideshare.net/mstfdemirdag/analytic-geometry-8693115. Accessed on: 4 March
2014
- Felipe, N, M. (2013). Analytic geometry basic concepts [PowerPoint Presentation]. Available at:
http://www.slideshare.net/NancyFelipe1/analytic-geometry-basic-concepts.Accessed on: 4
March 2014
- Marasigan, D. (2013). Lecture #2 analytic geometry [PowerPoint Presentation]. Available at:
http://www.slideshare.net/denmarmarasigan/lecture-2-analytic-geometry.Accessed on: 4
March 2014
- Marasigan, D. (2013). Lecture #3 analytic geometry [PowerPoint Presentation]. Available at:
http://www.slideshare.net/denmarmarasigan/lecture-3-analytic-geometry.Accessed on: 4
March 2014
- Marasigan, D. (2013). Lecture #5 analytic geometry [PowerPoint Presentation]. Available at:
http://www.slideshare.net/denmarmarasigan/lecture-5-analytic-geometry. Accessed on: 4
March 2014