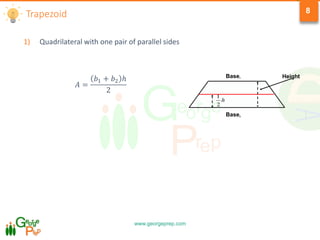
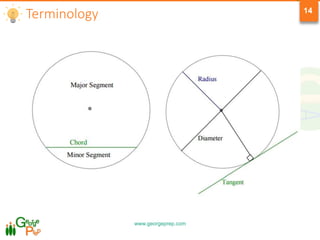
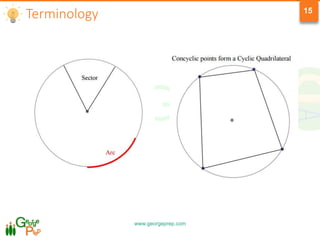
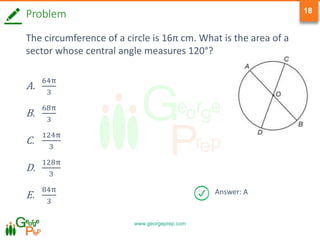
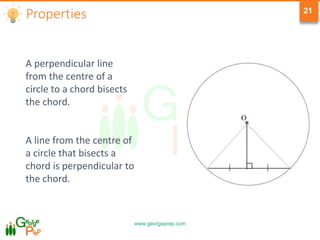
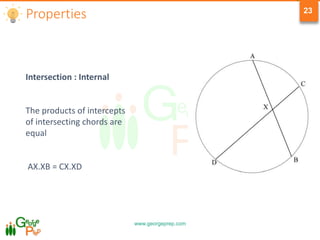
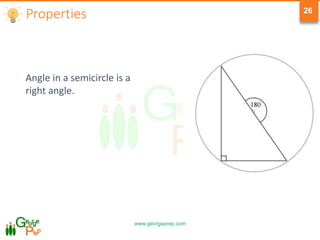
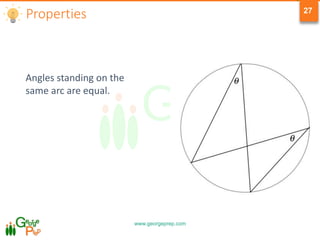
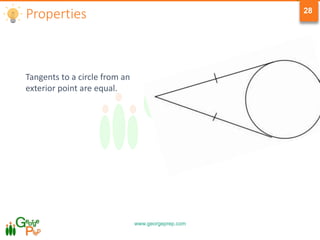
This document provides information on geometry concepts related to quadrilaterals, circles, and circle properties. It defines types of quadrilaterals like parallelograms, rhombuses, rectangles, squares, and trapezoids. It outlines key properties of these shapes. The document also defines circle terminology and explores properties of circles, including relationships between arcs, angles, chords, and tangents. It includes example problems testing the application of these geometric concepts.

1. www.georgeprep.com
0
Geometry Concept Session 2

2. www.georgeprep.com
1
Chapter Pathway
02
03
04
01
05
Triangle Properties
Polygons
Quadrilaterals
Circle Properties
Mensuration

3. www.georgeprep.com
2
Quadrilaterals

4. www.georgeprep.com
3
Quadrilaterals
- a quadrilateral is a polygon with 4 sides.
Properties
Sum of internal angles = 360°
Sum of external angles = 360°

5. www.georgeprep.com
4Parallelogram
- A quadrilateral with two pairs of parallel sides
Properties
Opposite angles are equal
Adjacent angles are supplementary
Area
= 𝑎𝑏𝑠𝑖𝑛𝜃
= 𝑏𝑎𝑠𝑒 𝑥 ℎ𝑒𝑖𝑔ℎ𝑡
Diagonal
Properties
Equal
Bisect each
other
Bisect at 90°
Bisect Vertex
angles
Parallelogram - yes - -

6. www.georgeprep.com
5Rhombus
1) A parallelogram with all four sides equal
Area
=
𝑑1 × 𝑑2
2
Diagonal
Properties
Equal
Bisect each
other
Bisect at 90°
Bisect Vertex
angles
Rhombus - yes yes yes

7. www.georgeprep.com
6Rectangle
1) A parallelogram with all four internal angles equal ( 90°)
Area = 𝑙𝑒𝑛𝑔𝑡ℎ × 𝑏𝑟𝑒𝑎𝑑𝑡ℎ
Perimeter = 2 𝑙 + 𝑏
Diagonal = 𝑙2 + 𝑏2
Diagonal
Properties
Equal
Bisect each
other
Bisect at 90°
Bisect Vertex
angles
Rectangle yes yes - -
𝑙
𝑏

8. www.georgeprep.com
7Square
1) Rectangle + Rhombus
Area = 𝑠2
Perimeter = 4𝑠
Diagonal = 2 𝑠
Diagonal
Properties
Equal
Bisect each
other
Bisect at 90°
Bisect Vertex
angles
Square yes yes yes yes
𝑠
𝑠

9. www.georgeprep.com
8Trapezoid
1) Quadrilateral with one pair of parallel sides
Base1
Base2
Height
𝐴 =
𝑏1 + 𝑏2 ℎ
2

10. www.georgeprep.com
9
Answer: B
Quantity A Quantity B
Area of a rectangle with perimeter
60cm
230 sq. cm
Problems

11. www.georgeprep.com
10
Answer: C
Problems
The height of a trapezoid is 6 meters. One of its bases is 8 meters. The area
of the trapezoid is 54 square meters. Find the other base.
A. 1
B. 5
C. 10
D. 15
E. 12

12. www.georgeprep.com
11
Answer: C
Problems
Four squares are joined together to form one large square. If the perimeter
of one of the original squares was 8x units, what is the length of the
diagonal of the new, larger square?
A. 16√2 x units
B. 2√2 x units
C. 4√2 x units
D. 8√2 x units
E. 64x units

13. www.georgeprep.com
12
Answer: B
Problems
Angle A of rhombus ABCD measures 120°. If one side of the rhombus is 10
units, what is the length of the longer diagonal?
A. √3 units
B. 10√3 units
C. 5√3 units
D. 20√3 units
E. 15√3 units

14. www.georgeprep.com
13
Circles

15. www.georgeprep.com
14
Terminology

16. www.georgeprep.com
15
Terminology

17. www.georgeprep.com
16
Properties
Equal arcs subtend equal
angels at the centre of the
circle.
If two arcs subtend equal
angles at the centre of the
circle, then the arcs are
equal.
𝑙 = 𝑟𝜃

18. www.georgeprep.com
17
Properties
𝐷𝑖𝑎𝑚𝑒𝑡𝑒𝑟 = 2𝑟
𝐴𝑟𝑒𝑎 = 𝜋𝑟2
𝐶𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒 = 2𝜋𝑟
𝐴𝑟𝑒𝑎 𝑜𝑓 𝑎 𝑠𝑒𝑐𝑡𝑜𝑟 =
𝜃
360
𝜋𝑟2
𝐿𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑡ℎ𝑒 𝑎𝑟𝑐 𝑜𝑓 𝑡ℎ𝑒 𝑠𝑒𝑐𝑡𝑜𝑟 =
𝜃
360
2𝜋𝑟
𝜃

19. www.georgeprep.com
18
Problem
The circumference of a circle is 16π cm. What is the area of a
sector whose central angle measures 120°?
A.
64π
3
B.
68π
3
C.
124π
3
D.
128π
3
E.
84π
3
Answer: A

20. www.georgeprep.com
19
Problem
A circular rim 72 inches in diameter rotates the same number of
inches per second as a circular rim 90 inches in diameter. If the
smaller rim makes 𝑥 revolutions per second, how many
revolutions per minute does the larger rim makes in terms of 𝑥 ?
A. 48π/x
B.
4x
5
C. 48x
D. 24x
E. x/75
Answer: C

21. www.georgeprep.com
20
Properties
Equal chords subtend equal
angles at the centre of the
circle.
Equal angles subtended at
the centre of the circle cut
off equal chords.

22. www.georgeprep.com
21
Properties
A perpendicular line
from the centre of a
circle to a chord bisects
the chord.
A line from the centre of
a circle that bisects a
chord is perpendicular to
the chord.

23. www.georgeprep.com
22
Properties
Equal chords are equidistant
from the centre of the circle.
Chords that are equidistant
from the centre are equal.

24. www.georgeprep.com
23
Properties
Intersection : Internal
The products of intercepts
of intersecting chords are
equal
AX.XB = CX.XD

25. www.georgeprep.com
24
Properties
Intersection : External
The square of the length of
the tangent from an
external point is equal to
the product of the
intercepts of the secant
passing through this point.
(AX)2 = BX.CX

26. www.georgeprep.com
25
Properties
The angle at the centre of a
circle is twice the angle at
the circumference
subtended by the same arc

27. www.georgeprep.com
26
Properties
Angle in a semicircle is a
right angle.

28. www.georgeprep.com
27
Properties
Angles standing on the
same arc are equal.

29. www.georgeprep.com
28
Properties
Tangents to a circle from an
exterior point are equal.

30. www.georgeprep.com
29
Problem
If a circle, regular pentagon and a regular octagon have the same
area and if the perimeter of the circle is represented by "c", that
of the pentagon by “p" and that of the octagon by "o", then which
of the following is true?
A. c > o > p
B. c > p > o
C. p > c > o
D. o > p > c
E. p > o > c
Answer: A

31. www.georgeprep.com
30
Problem
A Circle is inscribed in a equilateral triangle ABC such that point D
lies on the circle and on line segment AC and point E lies on circle
and on line segment AB. If line segment AB = 12, what is the area
of the figure created by line segments AD, AE and minor Arc DE.
A. 3√3 - (9/4) π
B. 3√3 – π
C. 36√3 - 12 π
D. 12√3 - 4 π
E. cannot be determined
Answer: D