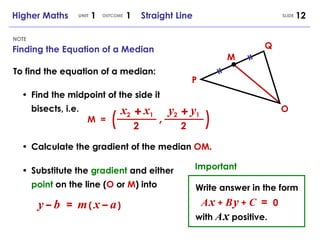
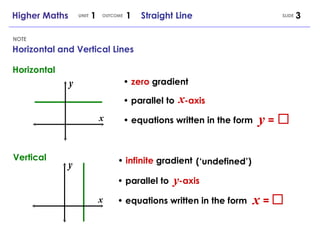
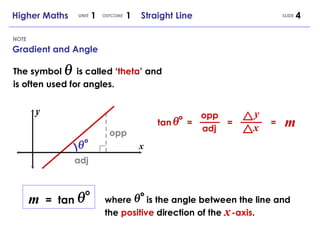
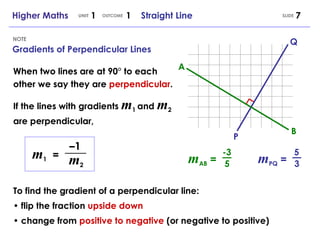
The document discusses various concepts relating to straight lines in mathematics including: 1) Calculating the gradient of a straight line between two points. 2) Horizontal and vertical lines having gradients of 0 or being undefined. 3) The relationship between gradient and angle of a line. 4) Finding the midpoint, collinearity of points, and gradients of perpendicular lines.

1. Higher Maths 1 1 Straight Line UNIT OUTCOME SLIDE

2. x 2 – x 1 Higher Maths 1 1 Straight Line Gradient of a Straight Line UNIT OUTCOME NOTE The symbol is called ‘ delta ’ and is used to describe change. Example (-2,7) (3,9) = 3 – (-2) = 5 Gradient m = x y x y 2 – y 1 = B ( x 2 , y 2 ) A ( x 1 , y 1 ) y 2 – y 1 x 2 – x 1 SLIDE

3. Horizontal and Vertical Lines NOTE • parallel to -axis y = x • parallel to -axis y y y (‘undefined’) Horizontal Vertical • equations written in the form • zero gradient • infinite gradient x = • equations written in the form Higher Maths 1 1 Straight Line UNIT OUTCOME SLIDE x x

4. The symbol is called ‘ theta ’ and is often used for angles. Gradient and Angle NOTE q tan q x y opp adj q = opp adj y x = m = tan = m Higher Maths 1 1 Straight Line UNIT OUTCOME SLIDE q where is the angle between the line and the positive direction of the -axis . q x

5. Finding the Midpoint NOTE The midpoint M of two coordinates is the point halfway in between and can be found as follows: Higher Maths 1 1 Straight Line UNIT OUTCOME ( ) M = 2 y 2 y 1 2 x 2 x 1 , • do the same again for the y -coordinate • add half of this distance to the first x -coordinate • write down the midpoint • find the distance between the x -coordinates An alternative method is to find the average of both coordinates: The Midpoint Formula + + M ( x 2 , y 2 ) ( x 1 , y 1 ) SLIDE

6. m PQ = Collinearity NOTE If points lie on the same straight line they are said to be collinear . Example Prove that the points P(-6,-5), Q(0,-3) and R(12,1) are collinear. (-3) – (-5) 0 – (-6) = = 2 6 1 3 m QR = 1 – (-3) 12 – 0 = = 4 12 1 3 m PQ = m QR The points are collinear. We have shown Higher Maths 1 1 Straight Line UNIT OUTCOME SLIDE

7. Gradients of Perpendicular Lines NOTE When two lines are at 90° to each other we say they are perpendicular . A B P Q m AB = -3 5 m PQ = 5 3 m 1 = m 2 – 1 If the lines with gradients m 1 and m 2 are perpendicular, To find the gradient of a perpendicular line: • flip the fraction upside down • change from positive to negative (or negative to positive) Higher Maths 1 1 Straight Line UNIT OUTCOME SLIDE

8. Different Types of Straight Line Equation NOTE Any straight line can be described by an equation. The equation of a straight line can be written in several different ways . y = m x + c Basic Equation (useful for sketching) A x + B y + C = 0 General Equation (always equal to zero) Straight lines are normally described using the General Equation , with as a positive number. A (not the -intercept!) y Higher Maths 1 1 Straight Line UNIT OUTCOME SLIDE

9. The Alternative Straight Line Equation NOTE y – b = m ( x – a ) for the line with gradient m x y ( x , y ) ( a , b ) x – a m = y – b Example Find the equation of the line with gradient and passing through (5,-2) . 1 2 y – ( - 2) = ( x – 5 ) 1 2 y + 2 = ( x – 5 ) 1 2 2 y + 4 = x – 5 x – 2 y – 9 = 0 Substitute: passing through ( a , b ) Higher Maths 1 1 Straight Line UNIT OUTCOME SLIDE

10. Straight Lines in Triangles NOTE An altitude is a perpendicular line between a vertex and the opposite side. A median is a line between a vertex and the midpoint of the opposite side. = = A perpendicular bisector is a perpendicular line from the midpoint of a side. Higher Maths 1 1 Straight Line UNIT OUTCOME SLIDE = =

11. Finding the Equation of an Altitude NOTE Higher Maths 1 1 Straight Line UNIT OUTCOME A B To find the equation of an altitude: • Find the gradient of the side it is perpendicular to ( ). m AB C • To find the gradient of the altitude, flip the gradient of AB and change from positive to negative: m altitude = m AB – 1 • Substitute the gradient and the point C into y – b = m ( x – a ) Important Write final equation in the form A x + B y + C = 0 with A x positive. SLIDE

12. Finding the Equation of a Median NOTE Higher Maths 1 1 Straight Line UNIT OUTCOME P Q To find the equation of a median: • Find the midpoint of the side it bisects, i.e. O • Calculate the gradient of the median OM . • Substitute the gradient and either point on the line ( O or M ) into y – b = m ( x – a ) Important Write answer in the form A x + B y + C = 0 with A x positive. = = M ( ) M = 2 y 2 y 1 2 x 2 x 1 , + + SLIDE