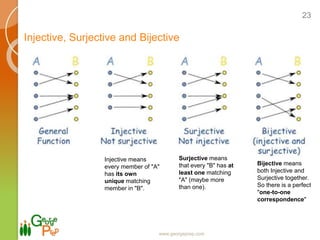
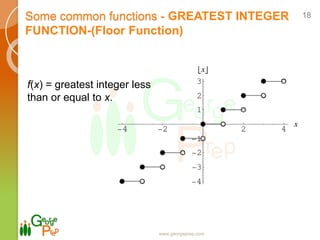
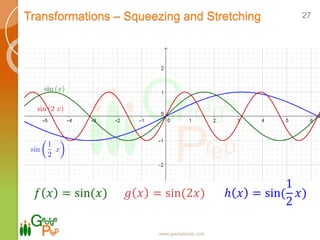
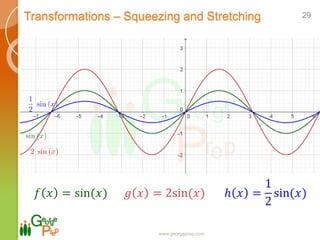
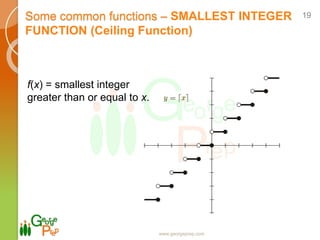
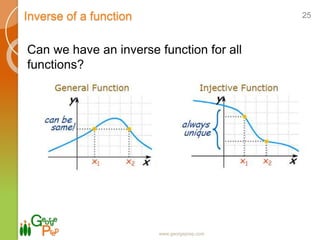
This document provides an overview of key concepts related to functions and graphs including: - The definitions of relations and functions and the differences between them - Common types of functions such as constant, identity, and absolute value functions - Transformations of graphs including vertical and horizontal shifts, squeezing and stretching - Properties of even, odd, and inverse functions - Techniques for finding the domain of a function - 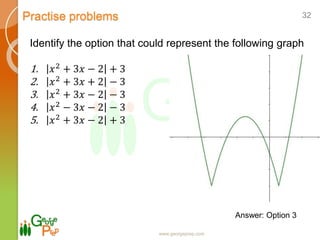Examples of problems involving functions and their solutions

1. www.georgeprep.com
1
Functions and Graphs - Concepts

2. www.georgeprep.com
2
Relations and Functions

3. Relation
www.georgeprep.com
3
- A relation is a correspondence between two sets where each
element in the first set, corresponds to at least one element in the
second set.

4. Relation – Domain, co-domain and Range
www.georgeprep.com
4

5. Function
www.georgeprep.com
5
- A relation in which each element in the domain corresponds to
exactly one element in the range.

6. Function – image and pre-
image
www.georgeprep.com
6
𝑓 𝑥 = 𝑦
Image = y
Pre-image = x

7. Relation Vs Function
www.georgeprep.com
7
Relation
Each input has at least one
output
Function
Each input has EXACTLY one output

8. Vertical Line test
www.georgeprep.com
8
A set of points in the xy-plane is the graph of a function if and only
if every vertical line intersects the graph in at most one point.

9. Finding Domain of a function
www.georgeprep.com
9
𝑓 𝑥 = 𝑦
Domain : The set of values of x for each of which the corresponding y is a real
number.
Situations where y will not be real
𝟐𝒏
𝑵𝒆𝒈𝒂𝒕𝒊𝒗𝒆 𝒏𝒖𝒎𝒃𝒆𝒓 Find the domain of
6
𝑥 − 4
q= 0 in
𝒑
𝒒 Find the domain of
𝟏𝟓
𝒙−𝟔
Involving Logarithmic function
In log 𝑎 𝑥
When a= 0/1/ -ve
When x = 0/-ve
Find the domain of log(𝑥−3) 80

10. Finding Domain of a function
www.georgeprep.com
10
Find the domain of the function,
f(x) =
𝑥
𝑥2+5𝑥+6
1)[0,∞)
2)(0, ∞)
3)(- ∞, -3] U [-2, ∞)
4)None of these
Answer: None of these

11. Finding Domain of a function
www.georgeprep.com
11
Find the domain of the function,
f(x) = log ( 7x – 12 – x2 )
1)[3,4)
2)(3 4)
3)(- ∞, -3] U [-4, ∞)
4)None of these
Answer: (3,4)

12. Some common functions - CONSTANT
FUNCTION
www.georgeprep.com
12
f(x) = b, b is any real
number.

13. Some common functions - IDENTITY FUNCTION
www.georgeprep.com
13
ƒ(𝑥) = 𝑥

14. Some common functions - SQUARE FUNCTION
www.georgeprep.com
14
𝑓(𝑥) = 𝑥2

15. Some common functions - CUBE FUNCTION
www.georgeprep.com
15
𝑓(𝑥) = 𝑥3

16. Some common functions - ABSOLUTE VALUE
FUNCTION
www.georgeprep.com
16
𝑓(𝑥) = |𝑥|

17. Some common functions - RECIPROCAL
FUNCTION
www.georgeprep.com
17
𝑓 𝑥 =
1
𝑥
, 𝑤ℎ𝑒𝑟𝑒 𝑥 ≠ 0

18. Some common functions - GREATEST INTEGER
FUNCTION-(Floor Function)
www.georgeprep.com
18
f(x) = greatest integer less
than or equal to x.

19. Some common functions – SMALLEST INTEGER
FUNCTION (Ceiling Function)
www.georgeprep.com
19
f(x) = smallest integer
greater than or equal to x.

20. Odd and Even functions
www.georgeprep.com
20
Symmetric with
Respect to
On Replacing x
with -x
Odd Function origin
ƒ(-x) = - ƒ(x)
Even Function y-axis ƒ(-x) = ƒ(x)

21. Odd and Even functions
www.georgeprep.com
21
Adding:
• Even + Even = even
• Odd + odd = odd
• Even + Odd = neither even nor odd (unless one function is zero).
Multiplying:
• Even * even = even function.
• Odd * odd = even function.
•The product of an even function and an odd function is an odd
function.

22. Problems
www.georgeprep.com
22
Determine whether the functions are even,
odd, or neither.
a. ƒ(𝑥) = 𝑥2 − 3
b. 𝑔(𝑥) = 𝑥5
+ 𝑥3
c. ℎ(𝑥) = 𝑥2 − 𝑥
Answer: Even, Odd and Neither
even nor odd

23. Injective, Surjective and Bijective
www.georgeprep.com
23
Injective means
every member of "A"
has its own
unique matching
member in "B".
Surjective means
that every "B" has at
least one matching
"A" (maybe more
than one).
Bijective means
both Injective and
Surjective together.
So there is a perfect
"one-to-one
correspondence"

24. Inverse of a function
www.georgeprep.com
24
- Pre-image and image interchange
Find the inverse of 𝑓 𝑥 = 4𝑥 + 3
Answer : 𝑓−1
𝑥 =
𝑥−3
4

25. Inverse of a function
www.georgeprep.com
25
Can we have an inverse function for all
functions?

26. Transformations – Vertical and Horizontal Shifts
www.georgeprep.com
26
Vertical Shift
To Graph Shift the Graph of ƒ(x)
ƒ(𝑥) + 𝑐 c units upward
ƒ 𝑥 − 𝑐 c units upward
Horizontal Shift
To Graph Shift the Graph of ƒ(x)
ƒ(𝑥 + 𝑐) c units to the left
ƒ 𝑥 − 𝑐 c units to the right

27. Transformations – Squeezing and Stretching
www.georgeprep.com
27
𝑓 𝑥 = sin(𝑥) 𝑔 𝑥 = sin(2𝑥) ℎ 𝑥 = sin(
1
2
𝑥)

28. Transformations – Squeezing and Stretching
www.georgeprep.com
28
In the direction of 𝒙
To Graph Shift the Graph of ƒ(x)
ƒ 𝑐𝑥 , c > 1 Compress in the direction of x
ƒ 𝑐𝑥 , 0 < c < 1 stretch in the direction of x
𝑓 𝑥 = sin(𝑥) 𝑔 𝑥 = sin(2𝑥) ℎ 𝑥 = sin(
1
2
𝑥)

29. Transformations – Squeezing and Stretching
www.georgeprep.com
29
𝑓 𝑥 = sin(𝑥) 𝑔 𝑥 = 2sin(𝑥) ℎ 𝑥 =
1
2
sin(𝑥)

30. Transformations – Squeezing and Stretching
www.georgeprep.com
30
In the direction of 𝒚
To Graph Shift the Graph of ƒ(x)
𝑐ƒ 𝑥 , c > 1 Stretch in the direction of y
𝑐ƒ 𝑥 , 0 < c < 1 Compress in the direction of y
𝑓 𝑥 = sin(𝑥) 𝑔 𝑥 = 2sin(𝑥) ℎ 𝑥 =
1
2
sin(𝑥)

31. Transformations – Reflections
www.georgeprep.com
31
Reflection along coordinate axis
To Graph Shift the Graph of ƒ(x)
−ƒ(𝑥) Reflect along x axis
ƒ −𝑥 Reflect along y axis

32. Practise problems
www.georgeprep.com
32
Identify the option that could represent the following graph
1. 𝑥2
+ 3𝑥 − 2 + 3
2. 𝑥2 + 3𝑥 + 2 − 3
3. 𝑥2 + 3𝑥 − 2 − 3
4. 𝑥2 − 3𝑥 − 2 − 3
5. 𝑥2 + 3𝑥 − 2 + 3
Answer: Option 3

33. Practise problems
www.georgeprep.com
33
Let 𝑓(𝑥) be a function satisfying 𝑓(𝑥)𝑓(𝑦) = 𝑓(𝑥𝑦) for all
real 𝑥, 𝑦. If f(2) = 4, then what is the value of 𝑓
1
2
?
1. 0
2. ¼
3. ½
4. 1/3
5. None of these
CAT 2008
Answer: 1/4

34. Practise problems
www.georgeprep.com
34
If 𝑎1 = 1and 𝑎 𝑛+1 = 2𝑎 𝑛 + 5, 𝑛 = 1,2 … , then 𝑎100 is
equal to
1. (5 × 299 – 6)
2. (5 × 299 + 6)
3. (6 × 299 + 5)
4. (6 × 299 − 5)
CAT 2000
Answer: Option 4

35. Practise problems
www.georgeprep.com
35
All points in the region R satisfy the inequality 𝑥 + 𝑦 +
𝑥 + 𝑦 ≤ 40. Find the area of region R
Answer: 600

36. Practise problems
www.georgeprep.com
36
Let 𝑓(𝑥) = max(2𝑥 + 1, 3 − 4𝑥), where 𝑥 is any real
number. Then the minimum possible value of 𝑓(𝑥) is:
1.
1
3
2. ½
3.
5
3
4.
4
3
5.
2
3
CAT 2006
Answer: Option 3