Uploaded byGeorge Prep
CAT Quadratic and Higher Order Equations
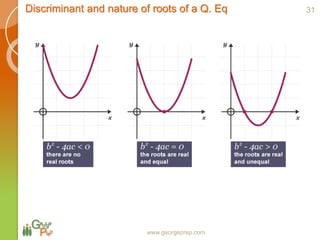
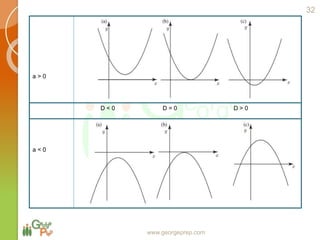
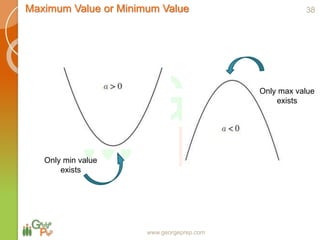
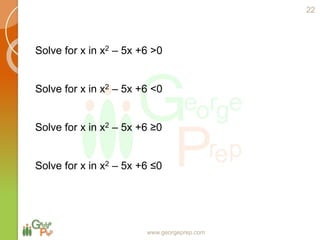This document discusses quadratic and higher order equations. It begins by introducing polynomials and classifying them based on coefficients and degree. Quadratic equations are then examined in more detail, including forming quadratic equations, finding roots using methods like the quadratic formula, and solving quadratic inequalities. The document also covers topics like the sum and product of roots, the discriminant and nature of roots, maximum/minimum values, common roots between equations, and relationships between coefficients and roots for higher order equations. Descartes' rule of signs is presented as a way to determine the number of positive and negative real roots of a polynomial equation.
More Related Content
![Unit 5 powerpoint[1] algebra (1)](https://cdn.slidesharecdn.com/ss_thumbnails/unit5powerpoint1algebra1-120804090149-phpapp02-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to CAT Quadratic and Higher Order Equations
More from George Prep
CAT Quadratic and Higher Order Equations
- 1. Quadratic and Higherorder Equations – Concept Session 1 www.georgeprep.com
- 2. Quadratic Equations Introduction toPolynomials Introduction to Quadratic Equations Forming Quadratic Equations Roots of a Quadratic Equation Solving Quadratic Inequalities Sum and Product of the roots Discriminant and the nature of roots Maximum and minimum value of a Quadratic expression Common roots Higher Order Equations Coefficients and roots Descartes rule of signs www.georgeprep.com Quadratic Equation 2
- 3. • Polynomials andtheir classification www.georgeprep.com 3
- 4. Polynomials www.georgeprep.com 𝑓(𝑥) = 𝑎1𝑥 𝑛 + 𝑎2 𝑥 𝑛−1 + ⋯ . 𝑎𝑛𝑥 is a polynomial in x, If 𝑎1, 𝑎2, 𝑎3…. are real numbers, 𝑥 is a real variable and 𝑛 is a whole number 4
- 5. Classification of Polynomials www.georgeprep.com A.On the basis of coefficients I. Polynomials over integers Eg: 3x2 + 4x + 9 II. Polynomials over rational numbers Eg: 3/5 x2 + 4x + 9 III. Polynomial over real numbers Eg: √3 x2 + √7 x +9 5
- 6. Classification of Polynomials www.georgeprep.com B.On the basis of number of terms I. Monomials Eg: 3x2 , √7 x II. Binomials Eg: 3/5 x2 + 4x III. Trinomials Eg: √3 x2 + √7 x +9 IV. Polynomials Usually more than three terms 6
- 7. www.georgeprep.com C. On thebasis of the degree I. Linear polynomial Eg: 4x+ 3y II. Quadratic Polynomial Eg: 4x2 +8xy III. Cubic polynomial Eg: 8 x3 + √7 x +9 III. Biquadratic polynomial Eg: 8 x4 + √7 x3 +9 7Classification of Polynomials
- 8.
- 9. Quadratic function andits Graph www.georgeprep.com 9
- 10. • Forming aQuadratic Equation www.georgeprep.com 10
- 11. Quadratic expression andquadratic equation www.georgeprep.com 11
- 12. Forming a quadraticequation www.georgeprep.com 1.When roots are given 2.When sum of the roots and the product of the roots are given 3.When the roots are related to the roots of another quadratic equation 12
- 13. Forming a quadraticequation www.georgeprep.com 1. When roots are given Form a quadratic equation whose roots are 1 and 2 13 Ans: 𝑥2 + 3𝑥 + 2 = 0
- 14. Forming a quadraticequation www.georgeprep.com 2. When sum of the roots and the product of the roots are given Form a quadratic equation such that the sum of the roots is 4 and the product of the roots is 3 14 Ans: 𝑥2 − 4𝑥 + 3 = 0
- 15. Forming a quadraticequation www.georgeprep.com 3. When the roots are related to the roots of another quadratic equation Form a quadratic equation whose roots are two more than the roots of the equation x2 - 3x +2 = 0 Changed roots Changed Q.Eq. 1 α + p and β + p a (x - p)2 + b (x - p) + c =0 2 α - p and β - p a (x + p)2 + b (x + p) + c =0 3 αp and βp a (x / p)2 + b (x / p) + c =0 4 α/p and β/p a (x p)2 + b (x p) + c =0 5 1/ α and 1/ β a (1/x )2 + b (1/x ) + c =0 6 -α and -β a (-x )2 + b (-x ) + c =0 a x 2 - b x + c =0 7 α2 and β2 ax + b root x + c =0 8 αn and βn ax2/n + bx1/n + c=0 15
- 16. • Roots ofa Quadratic Equation www.georgeprep.com 16
- 17. What is aroot of a quadratic equation? www.georgeprep.com 17
- 18. Finding roots ofa quadratic equation www.georgeprep.com 1. Splitting the middle term 2. Quadratic formula 18
- 19. Finding roots ofa quadratic equation www.georgeprep.com 1. Find the roots of the quadratic equation x2 + 5x + 6 = 0 2. Find the roots of the quadratic equation 6x2 - 5x - 6 = 0 19 Answers: 1. -2 or -3 2. 3/2 0r -2/3
- 20. Finding roots ofa quadratic equation www.georgeprep.com Find the roots of the quadratic equation x2 + 6x + 10 = 0 Quadratic Formula Roots = −𝑏 ± 𝑏2−4𝑎𝑐 2𝑎 20
- 21.
- 22. www.georgeprep.com Solve for xin x2 – 5x +6 >0 Solve for x in x2 – 5x +6 <0 Solve for x in x2 – 5x +6 ≥0 Solve for x in x2 – 5x +6 ≤0 22
- 23. www.georgeprep.com Solve for xin 𝑥2 – 5𝑥 + 6 (𝑥 + 2)(4𝑥 − 1) > 0 23 Answer: (−∞, −2) ∪ −1, ¼ ∪ (6, ∞)
- 24. • Sum andproduct of roots of a Quadratic Equation www.georgeprep.com 24
- 25. www.georgeprep.com Coefficients and thesum and product of roots 25
- 26. www.georgeprep.com Problems Form a quadraticequation with rational coefficients, one of whose roots is 4 + 3 26 Ans : 𝑥2 − 8𝑥 + 13 = 0
- 27. www.georgeprep.com Problems Find the valueof p if one root of the quadratic equation 𝑥2 – 12𝑥 – 𝑝 = 0 is twice the other 1) 32 2) -32 3) 390 4) 450 27 Answer: -32
- 28. www.georgeprep.com Problems Aakash and Kirannoted down a quadratic equation from the blackboard. Aakash made an error while noting down the coefficient of x and got the roots as 12 and 4, Kiran made an error in noting down the constant term and got the roots as 9 and 5. Which of the following is the actual equation? A. 𝑥2 − 14𝑥 + 14 = 0 B.2𝑥2 + 14𝑥 − 24 = 0 C. 𝑥2 − 14𝑥 + 48 = 0 D. 3𝑥2 − 17𝑥 + 48 = 0 28 Answer: Option C
- 29. • Discriminant andthe nature of roots www.georgeprep.com 29
- 30. www.georgeprep.com Discriminant of aquadratic expression 30
- 31. www.georgeprep.com Discriminant and natureof roots of a Q. Eq 31
- 32. www.georgeprep.com D < 0D = 0 D > 0 a > 0 a < 0 32
- 33. www.georgeprep.com Discriminant and natureof roots of a Q. Eq If the coefficients are rational, irrational roots occur in pairs. If the coefficients are real, complex roots occur in pairs. 33
- 34. www.georgeprep.com Problems If the rootsof 8 𝑚 𝑥2 + 8𝑥 + 32 𝑚 = 0 are real and equal, find the value of m 1. 2 2. ½ 3. ¾ 4. None of these 34 Answer: 1/2
- 35. www.georgeprep.com Problems How many equationsof the form 𝑥2 + 8𝑥 + 𝑚 exist such that the roots are real and 𝑚 is a positive integer? 1. 15 2. 16 3. 17 4. None of these 35 Answer: 16
- 36. • Maximum andminimum value of a Quadratic expression www.georgeprep.com 37
- 37. www.georgeprep.com Maximum Value orMinimum Value Only min value exists Only max value exists 38
- 38. www.georgeprep.com Maximum Value orMinimum Value Maximum of minimum value occurs at −𝑏 2𝑎 And the value is −𝐷 4𝑎 39
- 39. www.georgeprep.com Maximum Value orMinimum Value A quadratic function ƒ(x) attains a maximum of 3 at x = 1. The value of the function at x = 0 is 1. What is the value ƒ(x) at x = 10? 1. -119 2. -159 3. -110 4. -180 40 Answer : option 2
- 40.
- 41. www.georgeprep.com For twoquadratic equations 𝑎1 𝑥2 + 𝑏1 𝑥 + 𝑐1 = 0 and 𝑎2 𝑥2 + 𝑏2 𝑥 + 𝑐2 = 0 1. One common root when (𝑎1 𝑏2 − 𝑎2 𝑏1)(𝑏1 𝑐2 − 𝑏2 𝑐1) = (𝑐1 𝑎2 − 𝑐2 𝑎1)2 2. Two common roots when 𝑎1 𝑎2 = 𝑏1 𝑏2 = 𝑐1 𝑐2 42 Common roots
- 42. www.georgeprep.com Problems How many commonroots do 𝑥3 – 8𝑥2 − 6𝑥 − 9 = 0 and 𝑥3 – 7𝑥2 + 1𝑥 + 3 = 0 have? 1) 0 2) 1 3) 2 4) 3 43 Answer : option 1
- 43. • Higher OrderEquations www.georgeprep.com 44
- 44.
- 45. www.georgeprep.com Relationship between coefficientsand roots Consider the cubic equation 𝑎𝑥3 + 𝑏𝑥2 + 𝑐𝑥 + 𝑑 = 0 • Sum of roots = − 𝑏/𝑎 • Sum of all the three pairs of two roots taken at a time = c/a • Product of all the roots = - d/a 46
- 46. www.georgeprep.com Relationship between coefficientsand roots In general for any equation of degree n • Sum of roots = (-1)coefficient of x(n-1)/coefficient of xn • Sum of all the pairs of roots taken 2 at a time = coefficient of x(n-2)/coefficient of xn • Sum of roots taken r at a time = (-1)r coefficient of x(n-r)/coefficient of xn 47
- 47. Descartes's Rule ofsigns www.georgeprep.com 48
- 48. Number of positiveand negative real roots in a polynomial www.georgeprep.com 49
- 49. Problems www.georgeprep.com Use Descartes'Rule of Signs to determine the number of real roots of 𝑓 (𝑥) = 𝑥5 – 𝑥4 + 3𝑥3 + 9𝑥2 – 𝑥 + 5 50 Answer: 4 or 2 or 0 positive real roots and 1 negative real root
Editor's Notes
- #37 Substituting 2+ 3 in the equation and substituting the value of q, we get the value of p as 6+ 3 . Hence the other root is 4