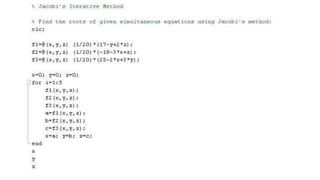
This document provides an overview of the Jacobi method for solving systems of linear equations. It includes the algorithm, an example, MATLAB code to implement the method, and applications in engineering. The Jacobi method makes approximations to solve systems of equations by iteratively solving for each variable. It converges to the solution when the last two iterations are identical. The method is useful for engineering problems involving linear systems and has advantages of being simple to program and stable, though it is slow compared to other methods.

1. PRESENTATION MATLAB
Sajjad Ahmad
2015-CH-241

2. Contents:
• Introduction of Jacobi Method
• Algorithm
• Example related algorithm
• Code for Jacobi Method
• Example with code
• Applications in Engineering
• Advantages and Disadvantages

3. Introduction:
• This method makes two assumptions:
1. that the system given by has a unique solution.
2. the coefficient matrix A has no zeros on its main diagonal.

4. • To begin the Jacobi method, solve the first equation for x1 the second
equation for x2 and so on, as follows.
• Then make an initial approximation of the solution,

5. Algorithm:

6. Example Related Algorithm:

7. • To begin, write the system in the form
• Initial Approximation because we do not know the actual solution

8. • As a convenient initial approximation. So, the first approximation is
• Continuing this procedure, you obtain the sequence of approximations
shown in Table

9. • Because the last two columns in Table are identical, you can conclude that to
three significant digits the solution is:
x1 = 0.186 x2 = 0.331 x3 =-0.423

10. Matlab Implementation for jacobi method:

11. Example with MATLAB Code:
20x+y-2z=17
3x+20y-z=-18
2x-3y+20z=25

13. Applications in Engineering:
• Efficient methods of solving systems of linear equations, especially when
approximate solutions are already known.
• Significantly reduce the amount of computation required.
• Plotting and analyzing mathematical relationships(2D and 3D)
• List and matrix operations
• Symbolic manipulation of equations
• Composition analysis of a distillation column system
• Temperature analysis for thermodynamics state equations

14. Advantages
• Fully diagonalizes a
symmetric matrix in one
iteration
• Easy to program
• Stable.
Disadvantages
• Works only for symmetric
matrices (but this is what
one needs for SVD)
• Slow

15. Little Thing is Big Thing