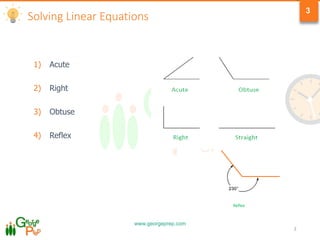
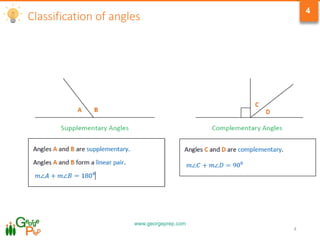
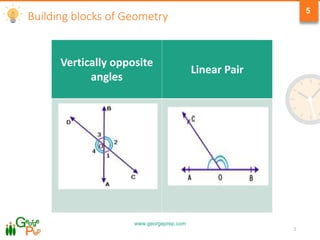
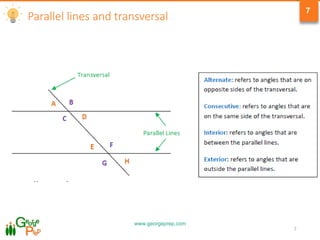
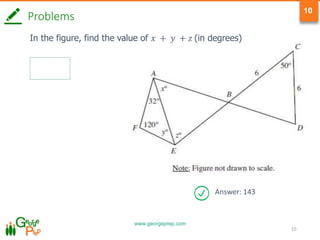
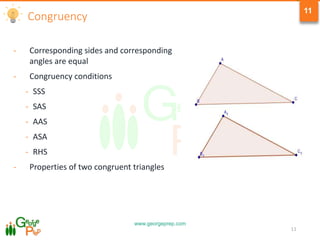
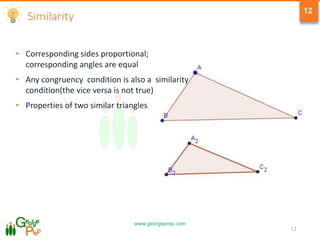
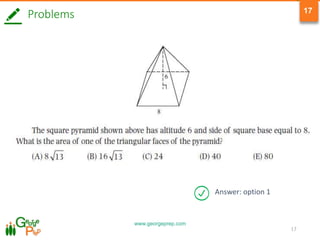
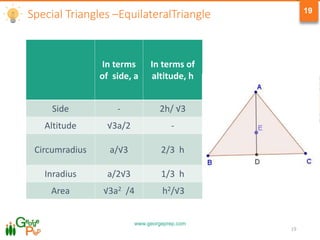
This document provides an overview of key geometry concepts covered in a lesson, including: 1) Classification of angles as acute, right, obtuse, or reflex 2) Properties of triangles such as internal angle sums, relationships between sides and angles, and triangle classification 3) Concepts of congruency, similarity, and properties of congruent and similar triangles 4) Special right triangles and their properties, including the Pythagorean theorem 5) Properties of polygons and calculations for polygon parameters and areas 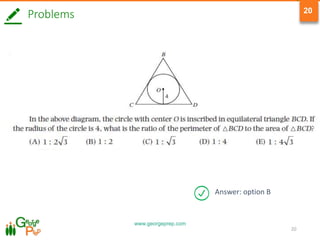6) Example problems are provided to demonstrate application of these concepts.

1. www.georgeprep.com
0
Geometry Concept Session 1
0

2. www.georgeprep.com
1
Chapter Pathway
02
03
04
01
05
Triangle Properties
Polygons
Quadrilaterals
Circle Properties
Mensuration
1

3. www.georgeprep.com
2
Building Blocks of Geometry
2

4. www.georgeprep.com
3
Solving Linear Equations
1) Acute
2) Right
3) Obtuse
4) Reflex
Reflex
3

5. www.georgeprep.com
4
Classification of angles
4

6. www.georgeprep.com
5
Building blocks of Geometry
Vertically opposite
angles
Linear Pair
5

7. www.georgeprep.com
6
Parallel lines and transversal
6

8. www.georgeprep.com
7
Parallel lines and transversal
7

9. www.georgeprep.com
8
Properties of Triangles
8

10. www.georgeprep.com
9
Triangle – Basic Properties
Basic Properties
• The sum of three internal angles = 180
• The sum of three exyernal angles = 360
• Exterior angle is equal to sum of interior opposite
Side related properties
• Sum of any two sides is greater than the third side
• Difference of any two sides is lesser than the third side
• Side opposite the greater angle is greater and vice versa
• Sides opposite equal angles are equal and vice versa
Classification
• On the basis of angles
• On the basis of sides
9

11. www.georgeprep.com
10
Problems
In the figure, find the value of 𝑥 + 𝑦 + 𝑧 (in degrees)
Answer: 143
10

12. www.georgeprep.com
11
Congruency
- Corresponding sides and corresponding
angles are equal
- Congruency conditions
- SSS
- SAS
- AAS
- ASA
- RHS
- Properties of two congruent triangles
11

13. www.georgeprep.com
12
Similarity
• Corresponding sides proportional;
corresponding angles are equal
• Any congruency condition is also a similarity
condition(the vice versa is not true)
• Properties of two similar triangles
12

14. www.georgeprep.com
13
Special Triangles and their Properties
13

15. www.georgeprep.com
14
Pythagoras theorem
Pythagoras triplets
14
Special Triangles – Right Angled Triangle

16. www.georgeprep.com
15
1) Special Right Angled triangles
15
90-60-30
triangle
90-45-45
triangle
Side Ratios 2: √3:1 √2 : 1: 1
Special Triangles – Right Angled Triangle

17. www.georgeprep.com
16
16
The perimeter of an isosceles right triangle is (32 + 32 2).
What is the length of the hypotenuse of the triangle?
A. 32
B. 16
C. 16 2
D.
32
2
E. 18
Problems

18. www.georgeprep.com
17
17
Problems
Answer: option 1

19. www.georgeprep.com
18
18
Problems
Answer: option 1

20. www.georgeprep.com
19
19
In terms
of side, a
In terms of
altitude, h
Side - 2h/ √3
Altitude √3a/2 -
Circumradius a/√3 2/3 h
Inradius a/2√3 1/3 h
Area √3a2 /4 h2/√3
Special Triangles –EquilateralTriangle

21. www.georgeprep.com
20
20
Problems
Answer: option B

22. www.georgeprep.com
21
Polygons and their properties
21

23. www.georgeprep.com
22
22
Parameter Properties
Sum of external angles 360
Sum of internal angles (n-2)180
No of sides
360
𝑒𝑥𝑡. 𝑎𝑛𝑔𝑙𝑒
No of diagonals 𝑛 𝑛 − 3
2
Area
Hexagon = 3√3
𝑎2
2
Octagon = 2a2 (1+ √2)
Polygons

24. www.georgeprep.com
23
The points of a six-pointed star consist of six identical equilateral
triangles, with each side 6 cm (see figure). What is the area of the
shaded region?
A. 54 3
B. 48 3
C. 64 3
D. 84 3
E. 108 3
23
6cm 6cm
Problems