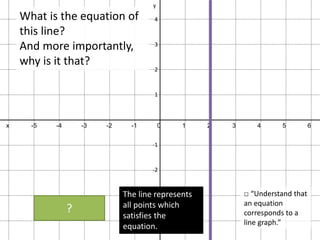
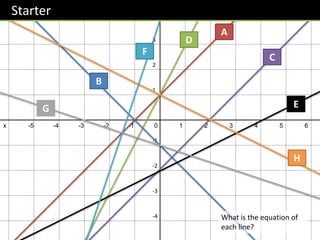
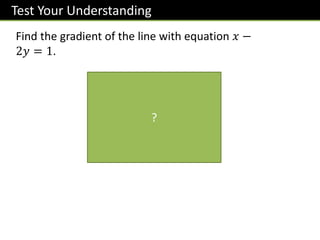
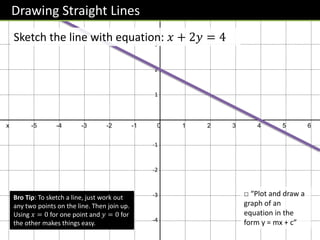
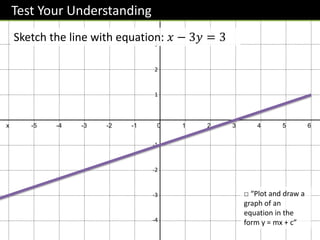
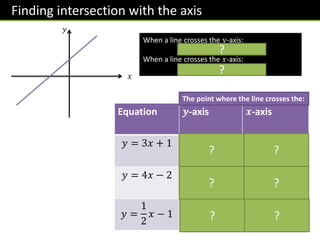
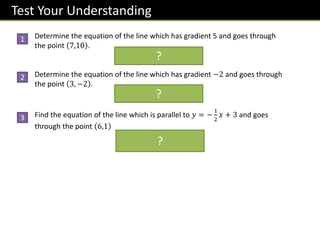
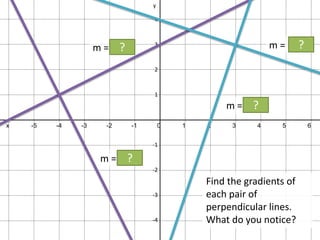
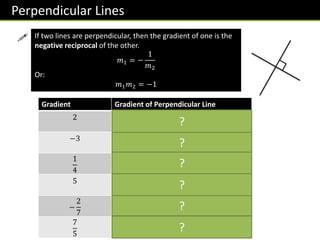
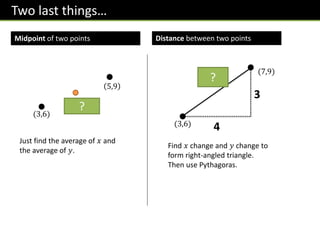
The document discusses key concepts for straight line equations in GCSE mathematics including: - Understanding that equations of the form y=mx+c correspond to straight line graphs - Plotting graphs from their equations and finding gradients and intercepts - Relating gradients to parallel and perpendicular lines - Generating equations for lines parallel or perpendicular to given lines - Finding gradients and equations from two points on a line

1. GCSE: Straight Line Equations
Dr J Frost (jfrost@tiffin.kingston.sch.uk)
www.drfrostmaths.com
Last modified: 30th August 2015

2. GCSE specification:
 Understand that an equation of the form y = mx + c corresponds to a straight line graph
 Plot straight line graphs from their equations
 Plot and draw a graph of an equation in the form y = mx + c
 Find the gradient of a straight line graph
 Find the gradient of a straight line graph from its equation
 Understand that a graph of an equation in the form y = mx + c has gradient of m and a y intercept
of c (ie. crosses the y axis at c)
 Understand how the gradient of a real life graph relates to the relationship between the two
variables
 Understand how the gradients of parallel lines are related
 Understand how the gradients of perpendicular lines are related
 Understand that if the gradient of a graph in the form y = mx + c is m, then the gradient of a line
perpendicular to it will be -1/m
 Generate equations of a line parallel or perpendicular to a straight line graph

3. x -5 -4 -3 -2 -1 0 1 2 3 4 5 6
y
4
3
2
1
-1
-2
-3
-4
What is the equation of
this line?
And more importantly,
why is it that?
𝑥 = 2
?
□ “Understand that
an equation
corresponds to a
line graph.”
The line represents
all points which
satisfies the
equation.

4. x -5 -4 -3 -2 -1 0 1 2 3 4 5 6
y
4
3
2
1
-1
-2
-3
-4
A
B
C
D
E
F
G
H
Starter
What is the equation of
each line?

5. Equation of a line
Understand that an equation of the form 𝑦 = 𝑚𝑥 + 𝑐
corresponds to a straight line graph
The equation of a straight line is 𝑦 = 𝒎𝑥 + 𝒄
gradient y-intercept

6. Gradient using two points
Given two points on a line, the gradient is:
𝑚 =
𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑦
𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑥

1, 4 (3, 10) 𝑚 = 3
5, 7 (8, 1) 𝑚 = −2
2, 2 (−1, 10) 𝑚 = −
8
3
?
?
?

7. Gradient from an Equation
 Find the gradient of a straight line graph from its equation.
𝑦 = 1 − 2𝑥
Putting in form 𝒚 =
𝒎𝒙 + 𝒄:
𝒚 = −𝟐𝒙 + 𝟏
Gradient is -2
2𝑥 + 3𝑦 = 4
Putting in form 𝒚 =
𝒎𝒙 + 𝒄:
𝟑𝒚 = −𝟐𝒙 + 𝟒
𝐲 = −
𝟐
𝟑
𝒙 +
𝟒
𝟑
Gradient is −
𝟐
𝟑
? ?

8. Test Your Understanding
Find the gradient of the line with equation 𝑥 −
2𝑦 = 1.
𝟐𝒚 = 𝒙 − 𝟏
𝒚 =
𝟏
𝟐
𝒙 −
𝟏
𝟐
𝒎 =
𝟏
𝟐
?

9. Exercise 1
Determine the gradient of the lines
which go through the following
points.
3,5 , 5,11 𝒎 = 𝟑
−1,0 , 4,3 𝒎 =
𝟑
𝟓
2,6 , 5, −3 𝒎 = −𝟑
4,7 , 8,10 𝒎 =
𝟑
𝟒
1,1 , −2,4 𝒎 = −𝟏
3,3 , 4,3 𝒎 = 𝟎
4, −2 , 2, −4 𝒎 = 𝟏
−3,4 , 4,3 𝒎 = −
𝟏
𝟕
Determine the gradient of the lines
with the following equations:
𝑦 = 5𝑥 − 1 𝒎 = 𝟓
𝑥 + 𝑦 = 2 𝒎 = −𝟏
𝑦 − 2𝑥 = 3 𝒎 = 𝟐
𝑥 − 3𝑦 = 5 𝒎 =
𝟏
𝟑
2𝑥 + 4𝑦 = 5 𝒎 = −
𝟏
𝟐
2𝑦 − 𝑥 = 1 𝒎 =
𝟏
𝟐
2𝑥 = 3𝑦 − 7 𝒎 =
𝟐
𝟑
A line 𝑙1 goes through the points
(2,3) and 4,6 . Line 𝑙2 has the
equation 4𝑦 − 5𝑥 = 1. Which
has the greater gradient:
𝒎𝟏 =
𝟑
𝟐
𝒎𝟐 =
𝟓
𝟒
So 𝒍𝟏 has greater gradient.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
1
2
3
a
b
c
d
e
f
g
h
a
b
c
d
e
f
g

10. x -5 -4 -3 -2 -1 0 1 2 3 4 5 6
y
4
3
2
1
-1
-2
-3
-4
Sketch the line with equation: 𝑥 + 2𝑦 = 4
□ “Plot and draw a
graph of an
equation in the
form y = mx + c”
Drawing Straight Lines
Bro Tip: To sketch a line, just work out
any two points on the line. Then join up.
Using 𝑥 = 0 for one point and 𝑦 = 0 for
the other makes things easy.

11. x -5 -4 -3 -2 -1 0 1 2 3 4 5 6
y
4
3
2
1
-1
-2
-3
-4
Sketch the line with equation: 𝑥 − 3𝑦 = 3
□ “Plot and draw a
graph of an
equation in the
form y = mx + c”
Test Your Understanding

12. Finding intersection with the axis
Equation 𝒚-axis 𝒙-axis
𝑦 = 3𝑥 + 1 0,1
−
1
3
, 0
𝑦 = 4𝑥 − 2 0, −2 1
2
, 0
𝑦 =
1
2
𝑥 − 1
0, −1 2,0
The point where the line crosses the:
? ?
? ?
? ?
𝑥
𝑦
When a line crosses the 𝑦-axis:
𝒙 = 𝟎
When a line crosses the 𝑥-axis:
𝒚 = 𝟎
?
?

13. Equation given a gradient and point
The gradient of a line is 3. It goes through the point (4, 10). What
is the equation of the line?
𝒚 = 𝟑𝒙 − 𝟐
Start with 𝒚 = 𝟑𝒙 + 𝒄 (where 𝒄 is to be determined)
Substituting: 𝟏𝟎 = 𝟑 × 𝟒 + 𝒄
Therefore 𝒄 = −𝟐
?
The gradient of a line is -2. It goes through the point (5, 10). What
is the equation of the line?
𝒚 = −𝟐𝒙 + 𝟐𝟎 ?

14. Test Your Understanding
Determine the equation of the line which has gradient 5 and goes through
the point 7,10 .
𝒚 = 𝟓𝒙 − 𝟐𝟓
Determine the equation of the line which has gradient −2 and goes through
the point 3, −2 .
𝒚 = −𝟐𝒙 + 𝟒
Find the equation of the line which is parallel to 𝑦 = −
1
2
𝑥 + 3 and goes
through the point 6,1
𝒚 = −
𝟏
𝟐
𝒙 + 𝟒
?
?
?
1
2
3

15. Equation given two points
A straight line goes through the points (3, 6) and (5, 12). Determine
the full equation of the line.
(3,6)
(5,12)
Gradient: 3
Equation: 𝒚 = 𝟑𝒙 − 𝟑
?
?
A straight line goes through the points (5, -2) and (1, 0). Determine
the full equation of the line.
(5, -2)
(1,0)
Gradient: -0.5
Equation: 𝒚 = −
𝟏
𝟐
𝒙 +
𝟏
𝟐
?
?

16. Exercise 2
Determine the points where the
following lines cross the 𝑥 and 𝑦 axis.
𝑦 = 2𝑥 + 1 0,1 , −
1
2
, 0
𝑦 = 3𝑥 − 2 0, −2 ,
2
3
, 0
2𝑦 + 𝑥 = 5 0,
5
2
, 5,0
Using suitable axis, draw the line with
equation 2𝑥 + 𝑦 = 5.
A line has gradient 8 and goes
through the point 2,10 . Determine
its equation.
𝒚 = 𝟖𝒙 − 𝟔
A line has gradient −3 and goes
through the point 2,10 . Determine
its equation.
𝒚 = −𝟑𝒙 + 𝟏𝟔
Determine the equation of the line parallel
to 𝑦 = 6𝑥 − 3 and goes through the point
3,10 .
𝒚 = 𝟔𝒙 − 𝟖
Determine the equation of the line parallel
to 𝑦 = −
1
3
𝑥 + 1 and goes through the
point −9,5 .
𝒚 = −
𝟏
𝟑
𝒙 + 𝟐
Determine the equation of the lines which
go through the following pairs of points:
3,5 , 4,7 𝒚 = 𝟐𝒙 − 𝟏
4,1 , 6,7 𝒚 = 𝟑𝒙 − 𝟏𝟏
−2,3 , 4, −3 𝒚 = −𝒙 + 𝟏
0,3 , 3,5 𝒚 =
𝟐
𝟑
𝒙 + 𝟑
4, −1 , 2,4 𝒚 = −
𝟓
𝟐
𝒙 + 𝟗
1
2
3
5
6
4
7
5
2
5
𝑥
𝑦
?
?
?
?
?
?
?
?
?
?
?
?
?

17. x -5 -4 -3 -2 -1 0 1 2 3 4 5 6
y
4
3
2
1
-1
-2
-3
-4
Find the gradients of
each pair of
perpendicular lines.
What do you notice?
m = -2
m = 1/2 m = -1/3
m = 3
?
? ?
?

18. Perpendicular Lines
Gradient Gradient of Perpendicular Line
2
−
1
2
−3 1
3
1
4
-4
5
−
1
5
−
2
7
7
2
7
5
−
5
7
?
?
?
?
?
?
If two lines are perpendicular, then the gradient of one is the
negative reciprocal of the other.
𝑚1 = −
1
𝑚2
Or:
𝑚1𝑚2 = −1


19. Example Problems
A line is goes through the point (9,10) and is perpendicular to another line with
equation 𝑦 = 3𝑥 + 2. What is the equation of the line?
𝒚 − 𝟏𝟎 = −
𝟏
𝟑
𝒙 − 𝟗
A line 𝐿1 goes through the points 𝐴 1,3 and 𝐵 3, −1 . A second line 𝐿2 is
perpendicular to 𝐿1 and passes through point B. Where does 𝐿2 cross the x-axis?
𝟓, 𝟎
Are the following lines parallel, perpendicular, or neither?
𝑦 =
1
2
𝑥
2𝑥 − 𝑦 + 4 = 0
Neither. Gradients are
𝟏
𝟐
and 𝟐. But
𝟏
𝟐
× 𝟐 = 𝟏, not -1, so not perpendicular.
?
?
?
Q1
Q2
Q3

20. Exercise 3
A line 𝑙1 goes through the indicated point and
is perpendicular to another line 𝑙2. Determine
the equation of 𝑙1 in each case.
2,5 𝑙2: 𝑦 = 2𝑥 + 1 𝒍𝟏: 𝒚 = −
𝟏
𝟐
𝒙 + 𝟔
−6,3 𝑙2: 𝑦 = 3𝑥 𝒍𝟏: 𝒚 = −
𝟏
𝟑
𝒙 + 𝟏
0,6 𝑙2: 𝑦 = −
1
2
𝑥 − 1 𝒍𝟏: 𝒚 = 𝟐𝒙 + 𝟔
−9,0 𝑙2: 𝑦 = −
1
3
𝑥 + 1 𝒍𝟏: 𝒚 = 𝟑𝒙 + 𝟐𝟕
10,10 𝑙2: 𝑦 = −5𝑥 + 5 𝒍𝟏: 𝒚 =
𝟏
𝟓
𝒙 + 𝟖
𝐴 2,5 𝐵 4,9
Find the equation of the line which passes through B,
and is perpendicular to the line passing through both
A and B.
𝒚 = −
𝟏
𝟐
𝒙 + 𝟏𝟏
Line 𝑙1 has the equation 2𝑦 + 3𝑥 = 4. Line 𝑙2 goes
through the points (2,5) and (5,7). Are the lines
parallel, perpendicular, or neither?
𝒎𝟏 = −
𝟑
𝟐
𝒎𝟐 =
𝟐
𝟑
𝒎𝟏𝒎𝟐 = −𝟏 so perpendicular.
𝑥
𝑦
𝑙
Determine the equation of the line 𝑙.
Known point on 𝒍:
𝟐, 𝟎
So equation of 𝒍:
𝒚 =
𝟏
𝟐
𝒙 − 𝟏
𝑥
𝑙
Determine the equation of the line 𝑙.
𝒚 = −
𝟏
𝟑
𝒙 + 𝟓
1
2
4
5
?
?
?
?
?
?
?
?
3
?

21. GCSE specification:
 Understand that an equation of the form y = mx + c corresponds to a straight line graph
 Plot straight line graphs from their equations
 Plot and draw a graph of an equation in the form y = mx + c
 Find the gradient of a straight line graph
 Find the gradient of a straight line graph from its equation
 Understand that a graph of an equation in the form y = mx + c has gradient of m and a y intercept
of c (ie. crosses the y axis at c)
 Understand how the gradient of a real life graph relates to the relationship between the two
variables
 Understand how the gradients of parallel lines are related
 Understand how the gradients of perpendicular lines are related
 Understand that if the gradient of a graph in the form y = mx + c is m, then the gradient of a line
perpendicular to it will be -1/m
 Generate equations of a line parallel or perpendicular to a straight line graph

22. Two last things…
Midpoint of two points Distance between two points
(3,6)
5,9
(𝟒, 𝟕. 𝟓)
?
(3,6)
(7,9)
5
4
3
Find 𝑥 change and 𝑦 change to
form right-angled triangle.
Then use Pythagoras.
?
Just find the average of 𝑥 and
the average of 𝑦.

23. Past Exam Questions
See GCSEPastPaper_Solutions.pptx
GCSERevision_StraightLineEquations.docx