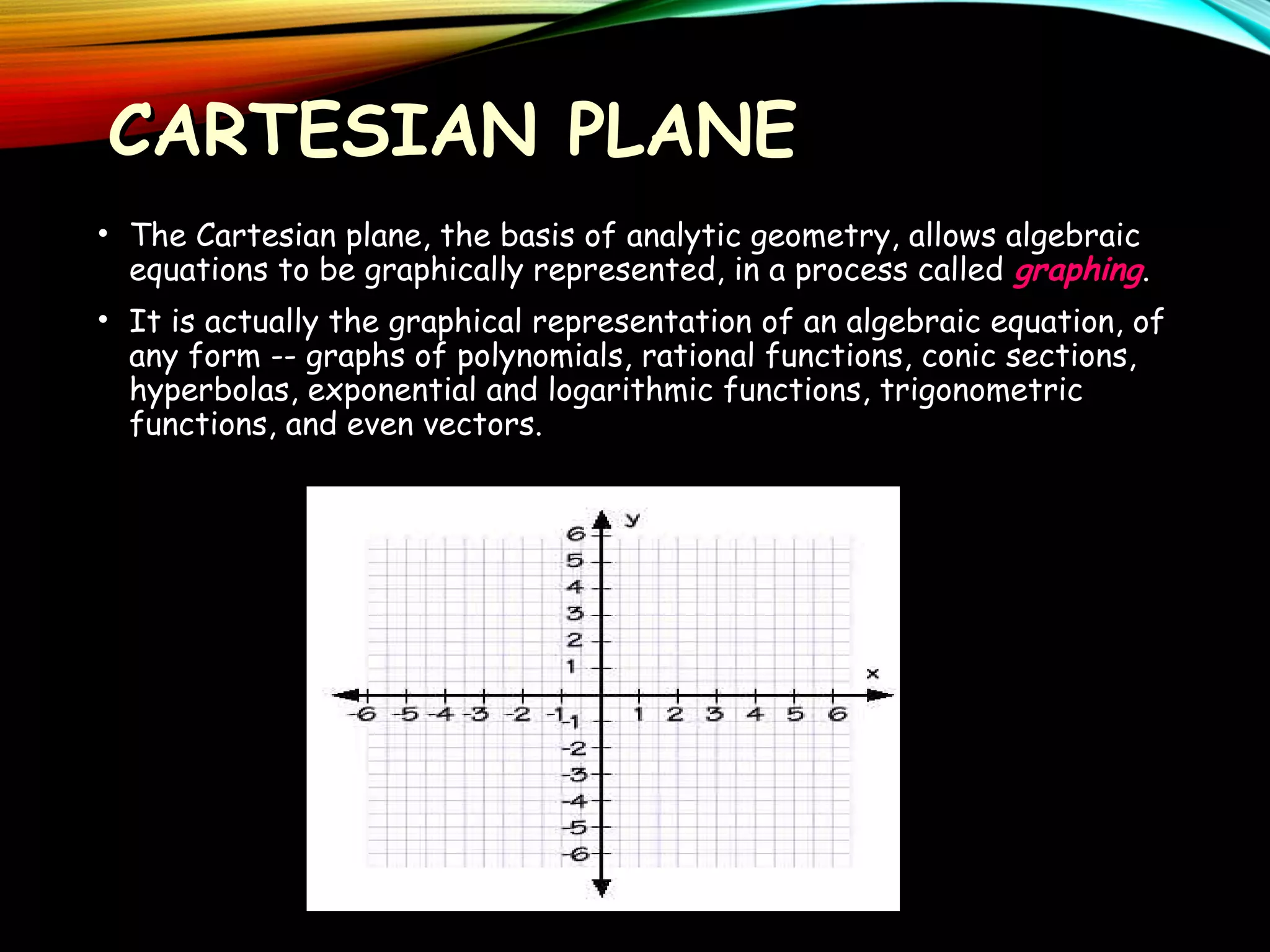
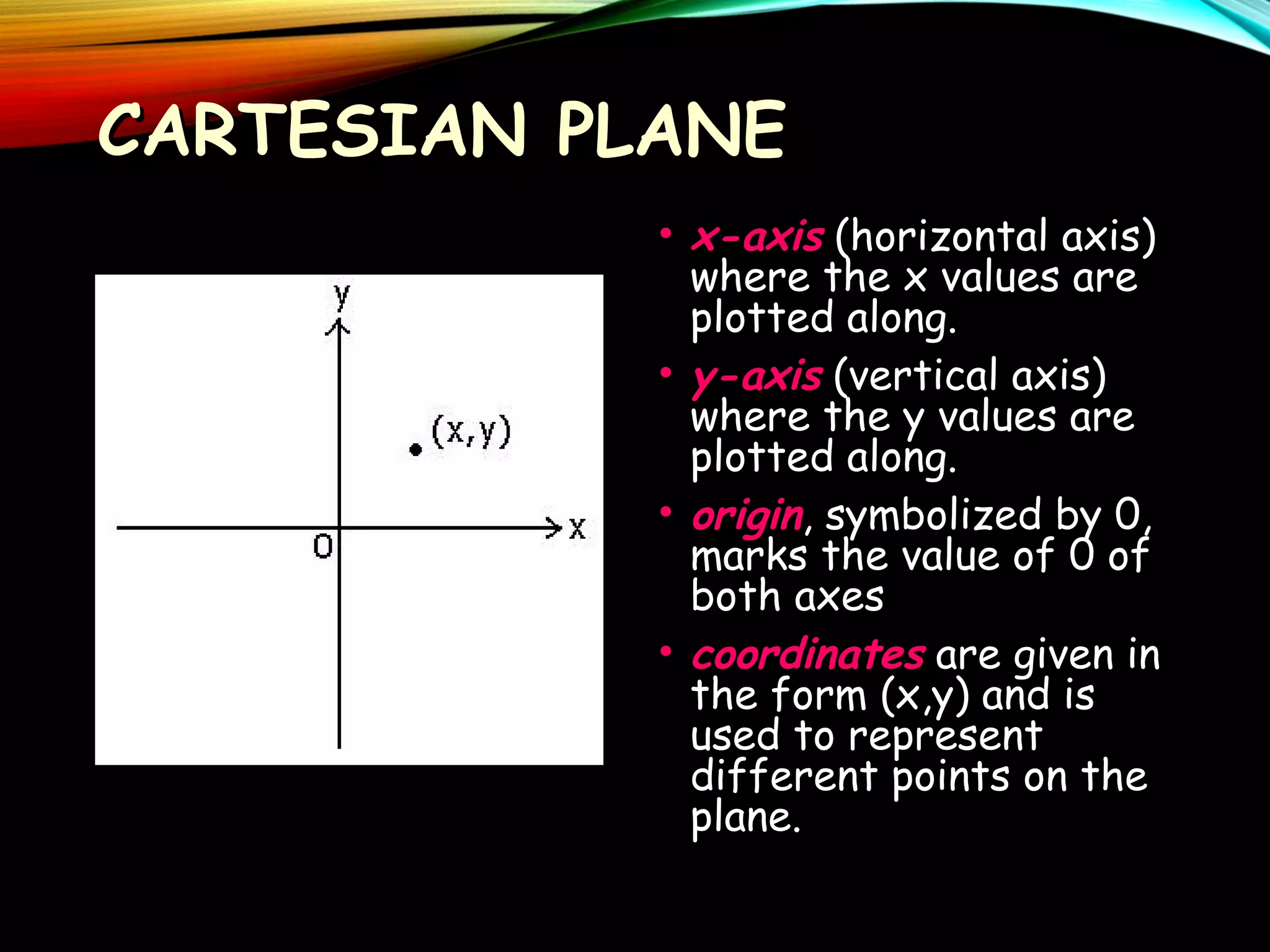
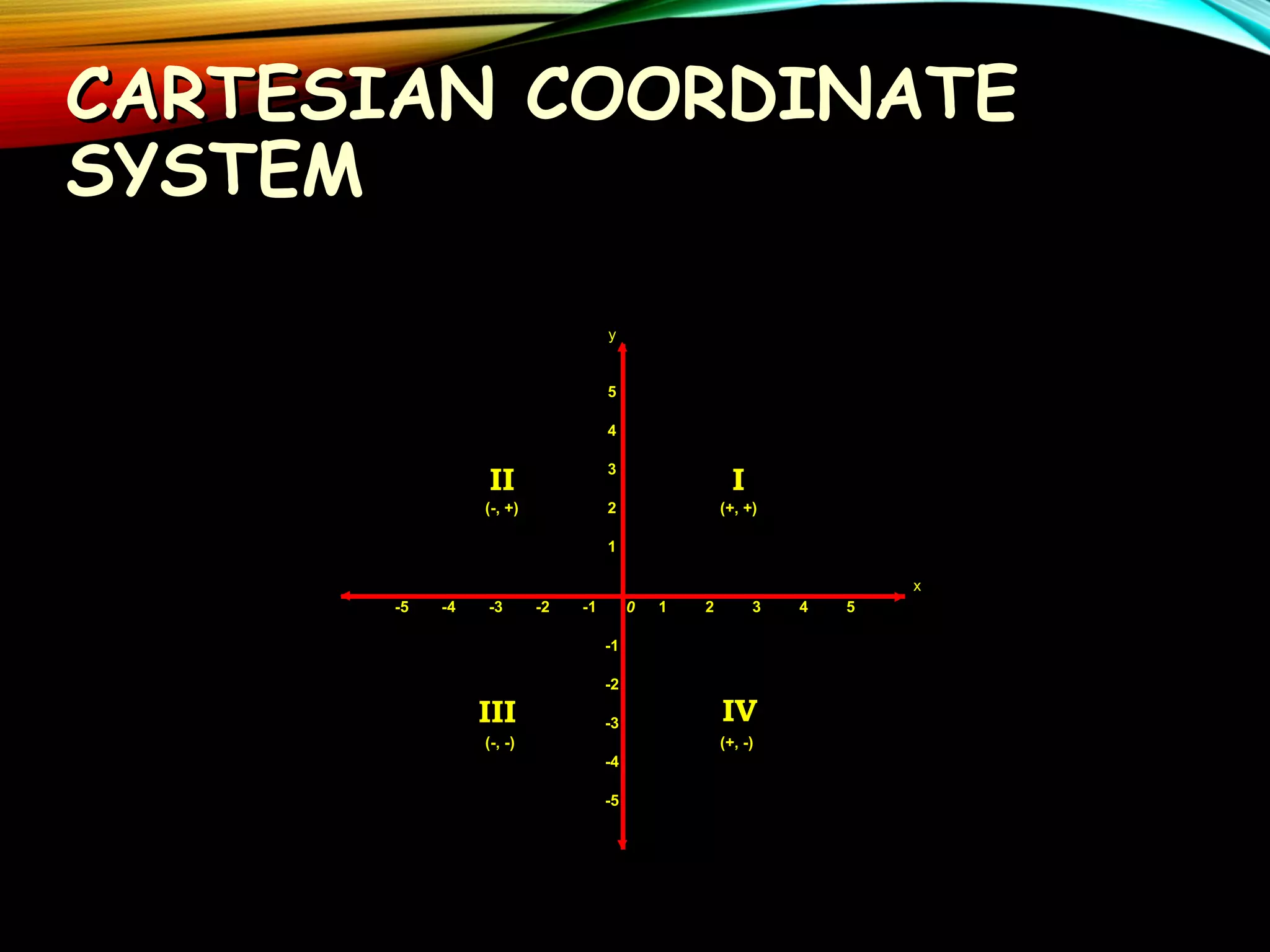
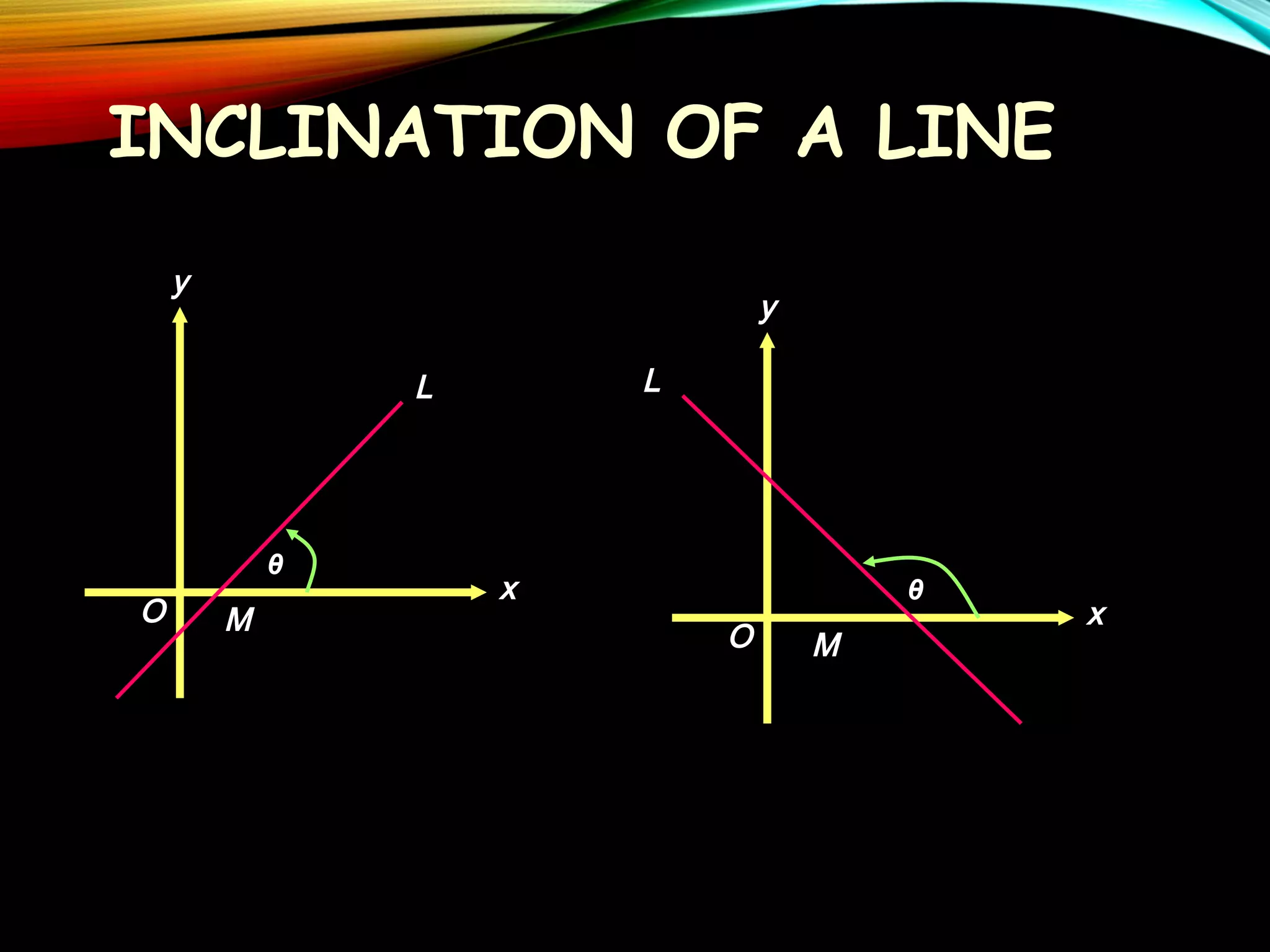
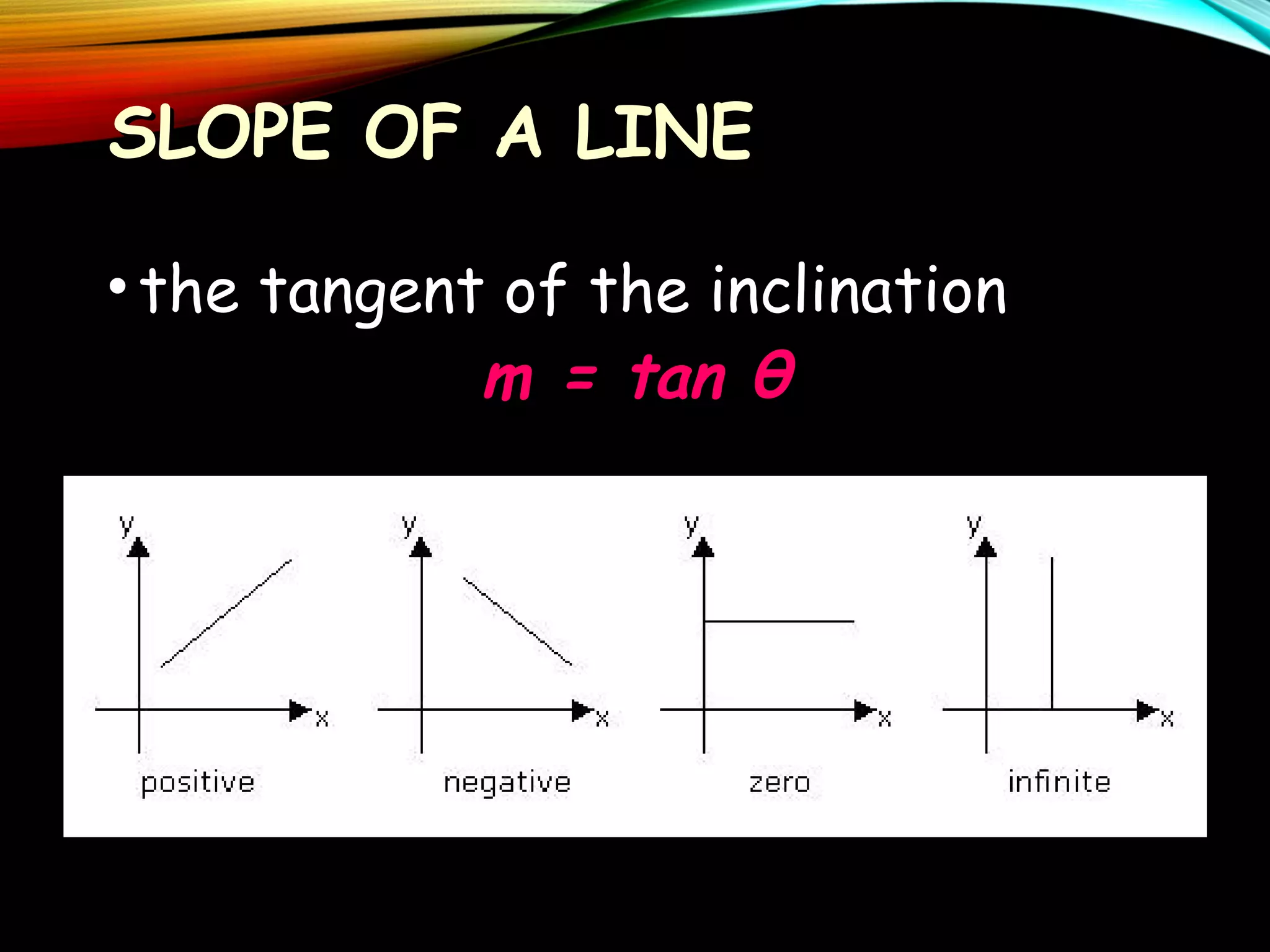
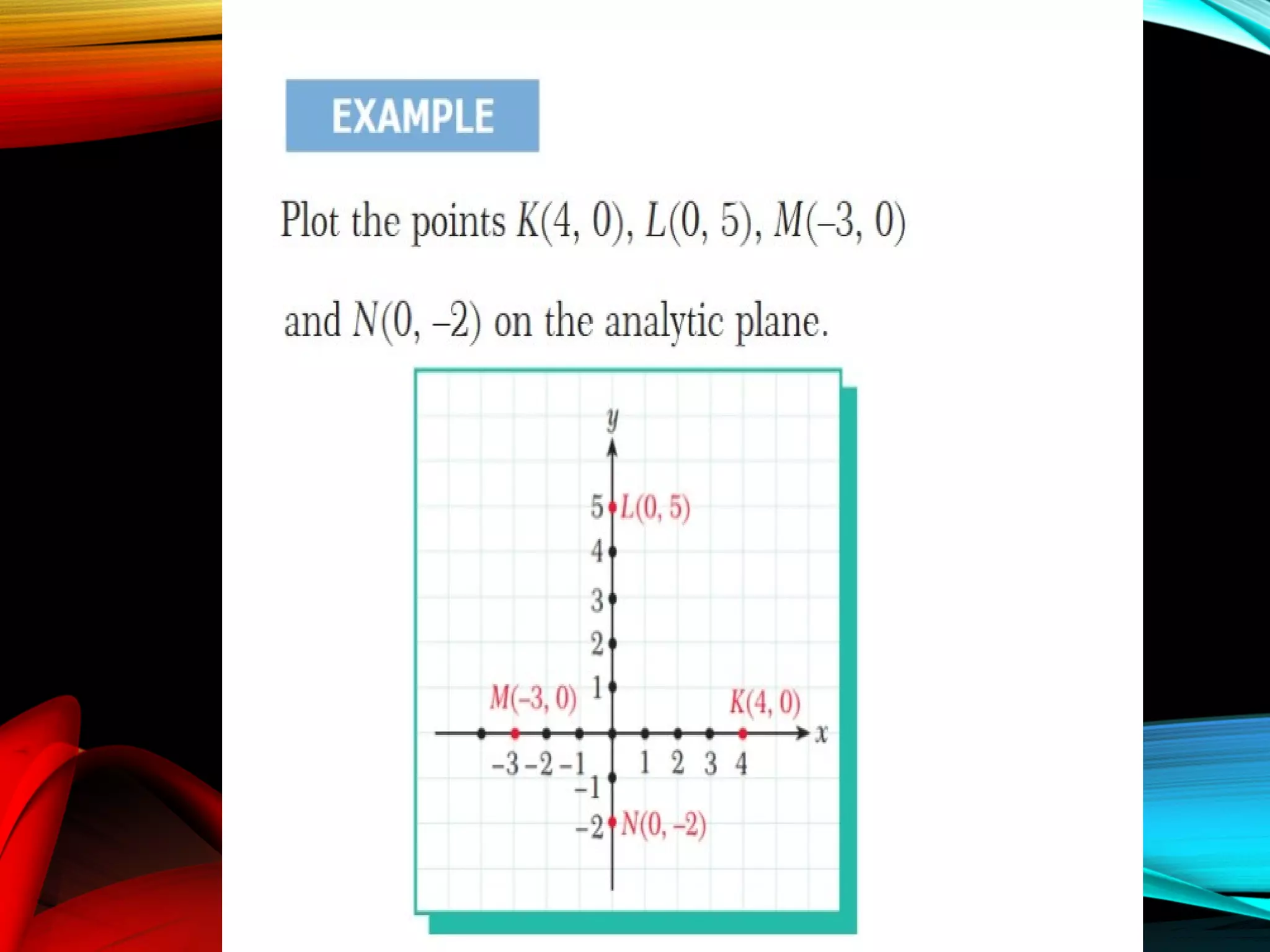
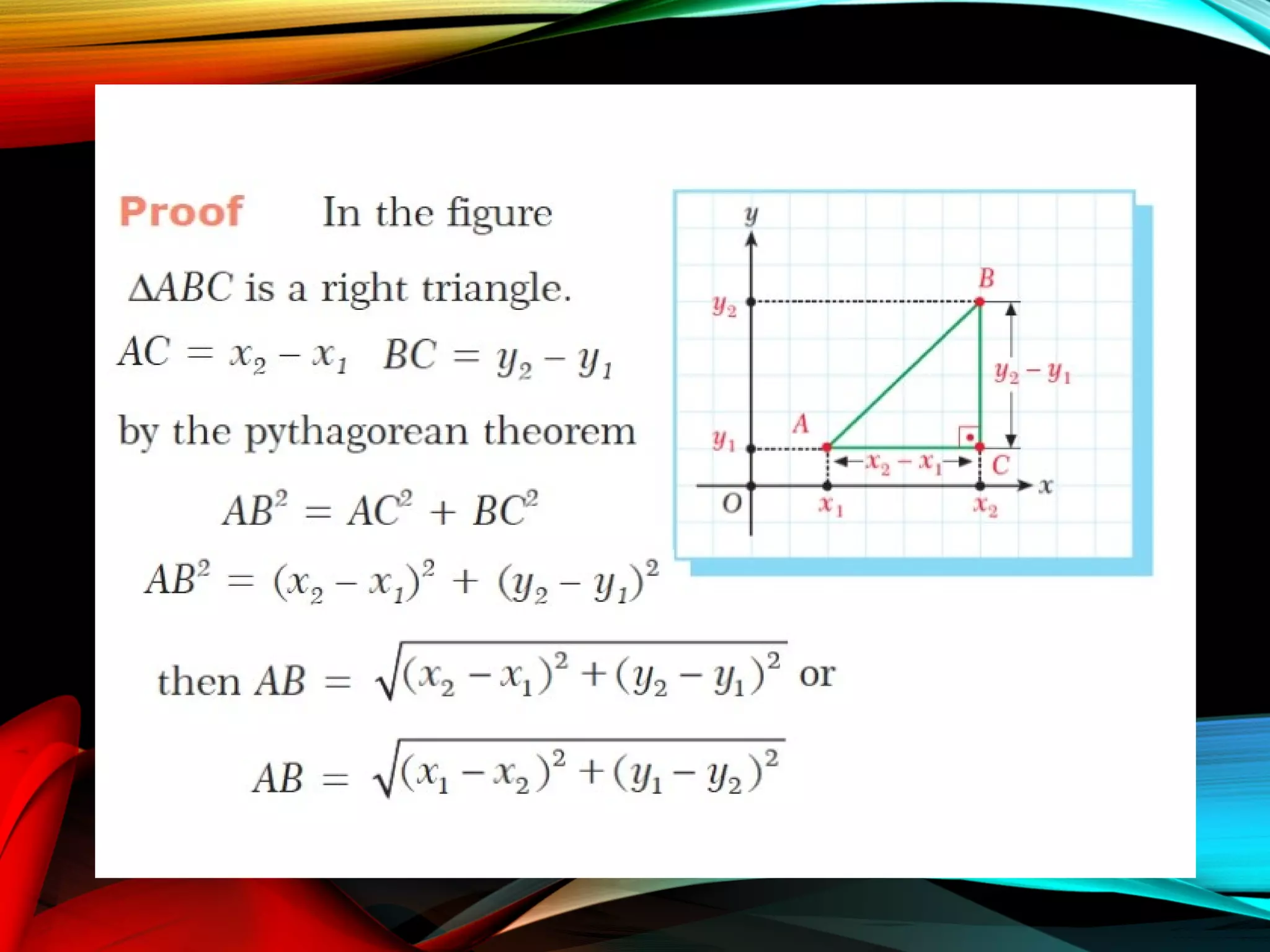
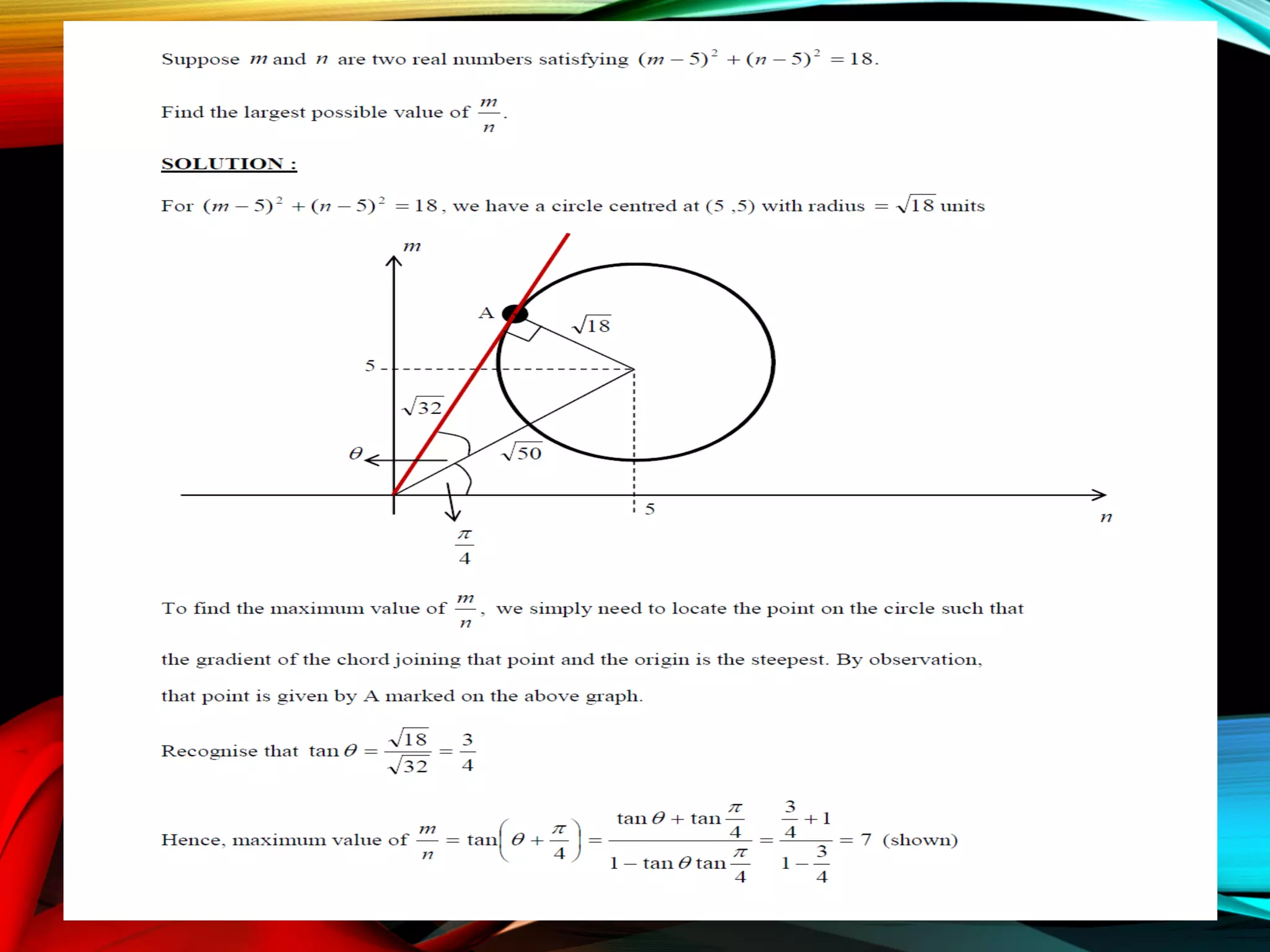
This document provides an overview of analytic geometry in 3 paragraphs or less. It introduces analytic geometry as a branch of mathematics that uses algebraic equations to describe geometric figures on a coordinate system. It was developed in the 1630s by Descartes and Fermat and allowed geometry and algebra to be linked by describing geometric concepts like points and lines with real numbers and equations. The key concept is using a coordinate system to assign unique real number coordinates to each point, allowing geometric shapes to be represented by algebraic equations.

1. DONE BY :SSM MASEKO
201124386

2. ANALYTIC GEOMETRY
BASIC CONCEPTS FOR
GRADE 10-12

3. ANALYTIC GEOMETRY
• a branch of mathematics which uses
algebraic equations to describe the size and
position of geometric figures on a
coordinate system.

4. ANALYTIC GEOMETRY
• It was introduced in the 1630s, an
important mathematical development,
for it laid the foundations for modern
mathematics as well as aided the
development of calculus.
• Rene Descartes (1596-1650) and
Pierre de Fermat (1601-1665),
French mathematicians, independently
developed the foundations for
analytic geometry.

5. ANALYTIC GEOMETRY
• the link between algebra and geometry was made possible by the
development of a coordinate system which allowed geometric
ideas, such as point and line, to be described in algebraic terms
like real numbers and equations.
• also known as Cartesian geometry or coordinate geometry.

6. ANALYTIC GEOMETRY
• the use of a coordinate system to relate geometric points
to real numbers is the central idea of analytic geometry.
• by defining each point with a unique set of real numbers,
geometric figures such as lines, circles, and conics can be
described with algebraic equations.

7. CARTESIAN PLANE
• The Cartesian plane, the basis of analytic geometry, allows algebraic
equations to be graphically represented, in a process called graphing.
• It is actually the graphical representation of an algebraic equation, of
any form -- graphs of polynomials, rational functions, conic sections,
hyperbolas, exponential and logarithmic functions, trigonometric
functions, and even vectors.

8. CARTESIAN PLANE
• x-axis (horizontal axis)
where the x values are
plotted along.
• y-axis (vertical axis)
where the y values are
plotted along.
• origin, symbolized by 0,
marks the value of 0 of
both axes
• coordinates are given in
the form (x,y) and is
used to represent
different points on the
plane.

9. CARTESIAN COORDINATE
SYSTEM
y
5
4
II
3
I
(-, +)
2
(+, +)
1
x
-5
-4
-3
-2
-1
0
1
2
3
-1
-2
III
-3
(-, -)
IV
(+, -)
-4
-5
4
5

10. CARTESIAN COORDINATE
SYSTEM
y
O
x

11. DISTANCE BETWEEN TWO
POINTS

12. MIDPOINT BETWEEN TWO
POINTS

13. INCLINATION OF A LINE
• The smallest angle θ, greater than
or equal to 0°, that the line makes
with the positive direction of the
x-axis (0° ≤ θ < 180°)
• Inclination of a horizontal line is 0.

14. INCLINATION OF A LINE
y
y
L
L
θ
O
M
x
θ
O
M
x

15. SLOPE OF A LINE
• the tangent of the inclination
m = tan θ

16. SLOPE OF A LINE
• passing through two given points,
P1(x1, y1) and P2 (x2, y2) is equal to
the difference of the ordinates
divided by the differences of the
abscissas taken in the same order

17. THEOREMS ON SLOPE
• Two non-vertical lines are parallel
if, and only if, their slopes are
equal.
• Two slant lines are perpendicular
if, and only if, the slope of one is
the negative reciprocal of the
slope of the other.

18. ANGLE BETWEEN TWO
LINES

19. ANGLE BETWEEN TWO
LINES
• If θ is angle, measured counterclockwise, between two lines,
then
• where m2 is the slope of the terminal side and m1 is the slope
of the initial side

25. data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wCEAAkGBhQRERUUExQVFB
REFERENCE LIST
http://stochastix.wordpress.com/
2009/07/28/analytical-geometrywith-pov-ray/
data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wCEAAkGBhQRE
RUUExQVFB
http://2.bp.blogspot.com/mj2uk1BZPAY/ULPFumUCmxI/AAAAAAAAKrA/I78
osDm1nPw/s400/math1.gif
This work belongs
to NancyFelipe And Mustafa
Demirdag and google images