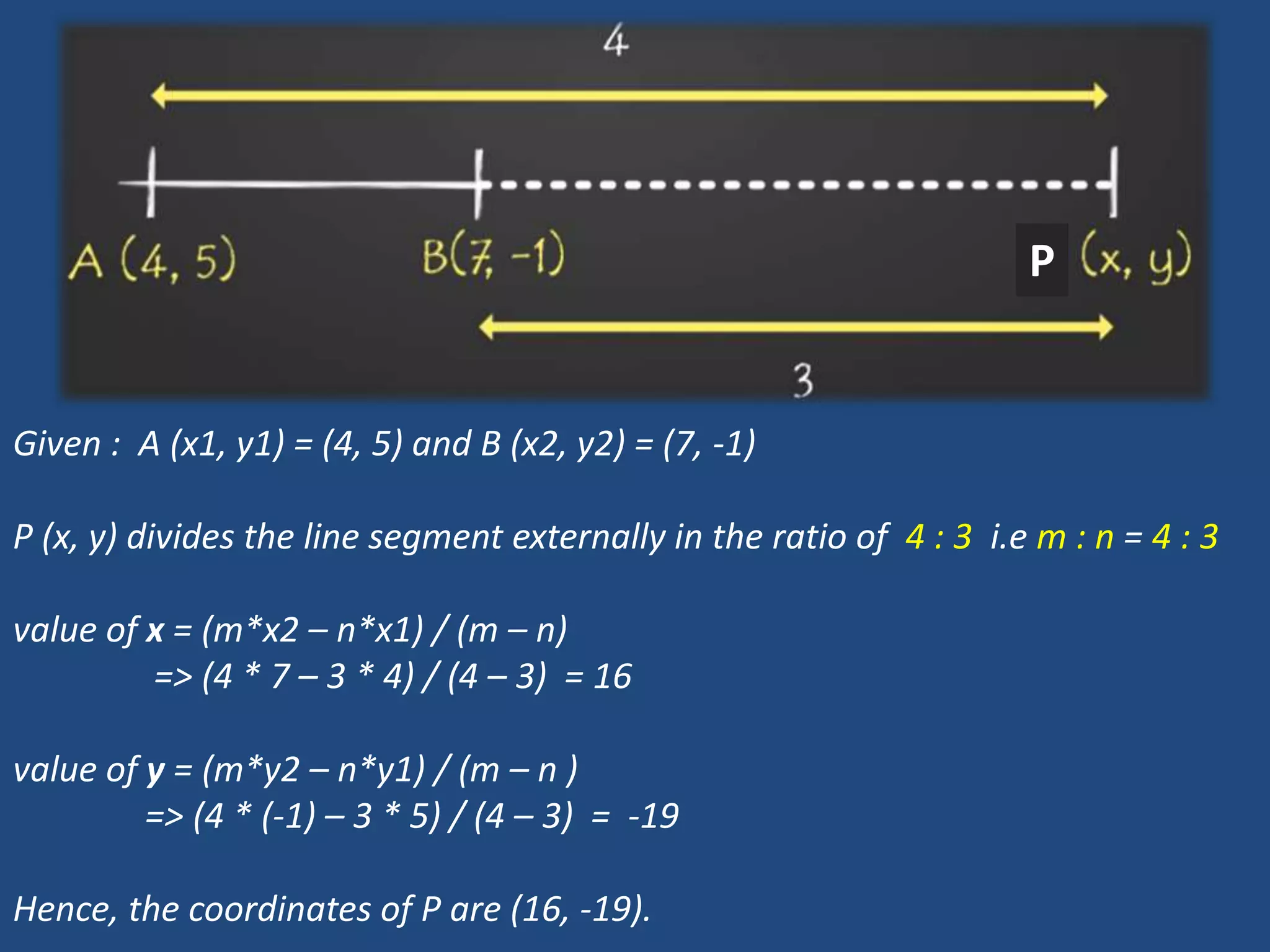
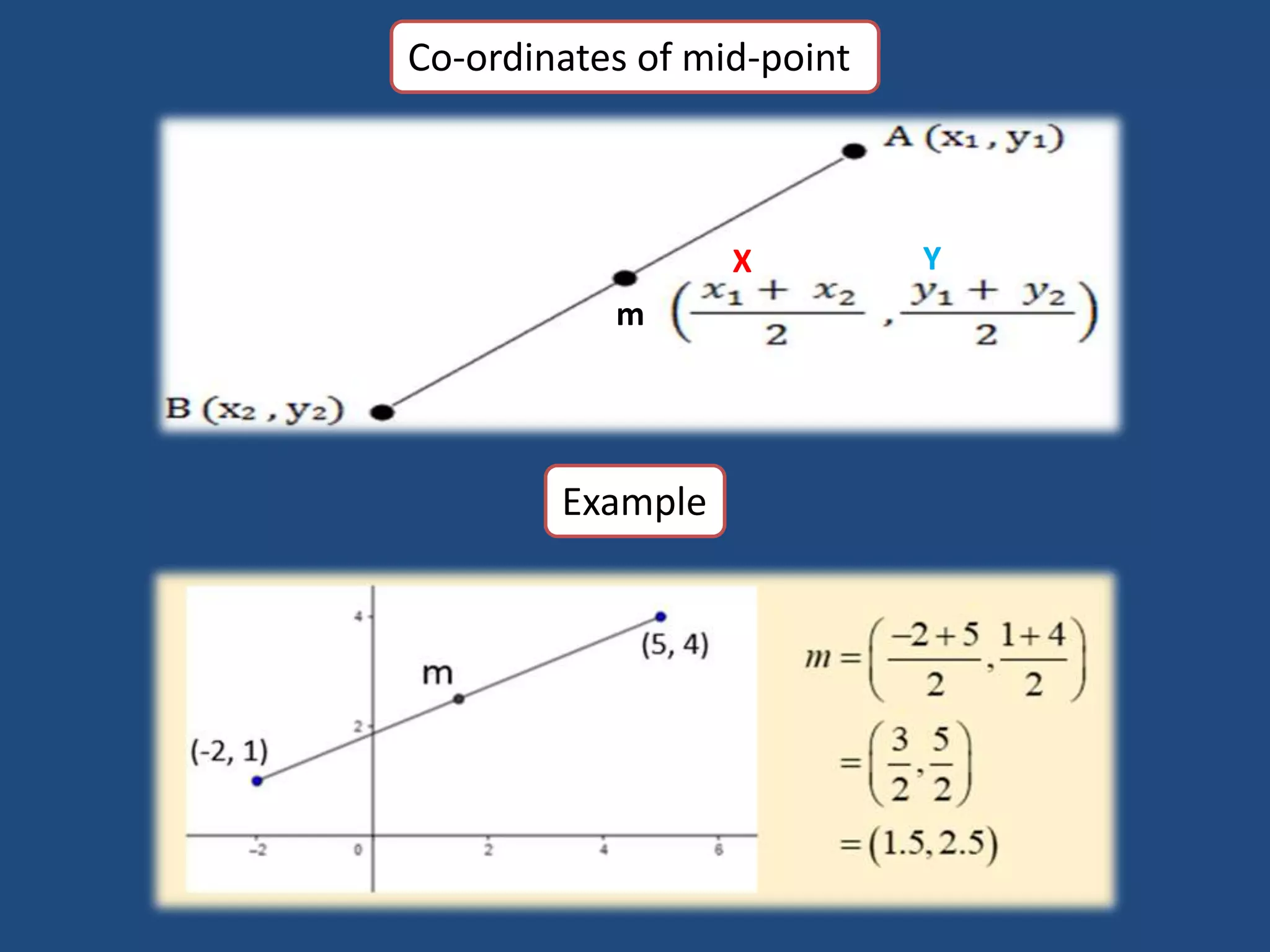
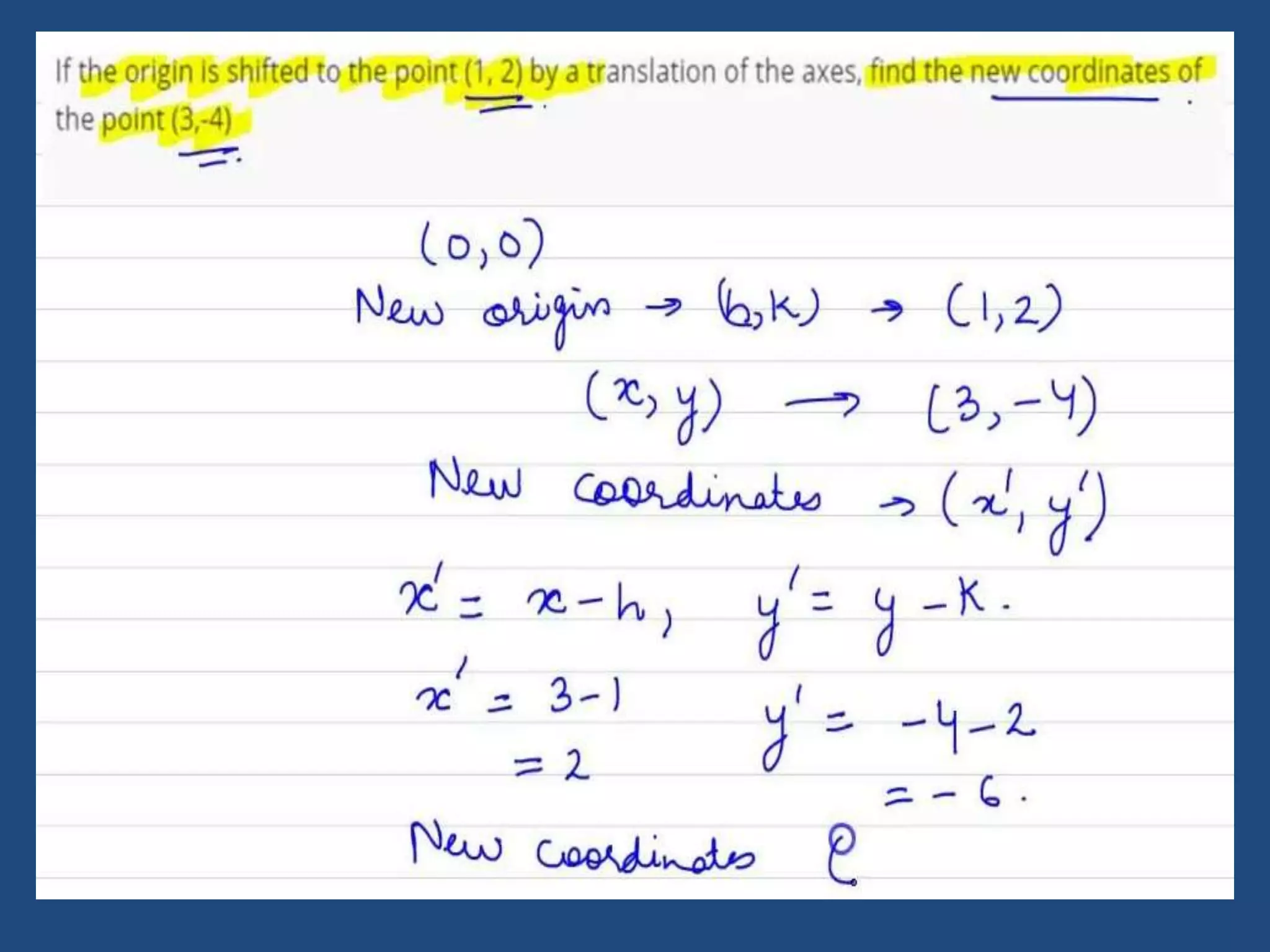
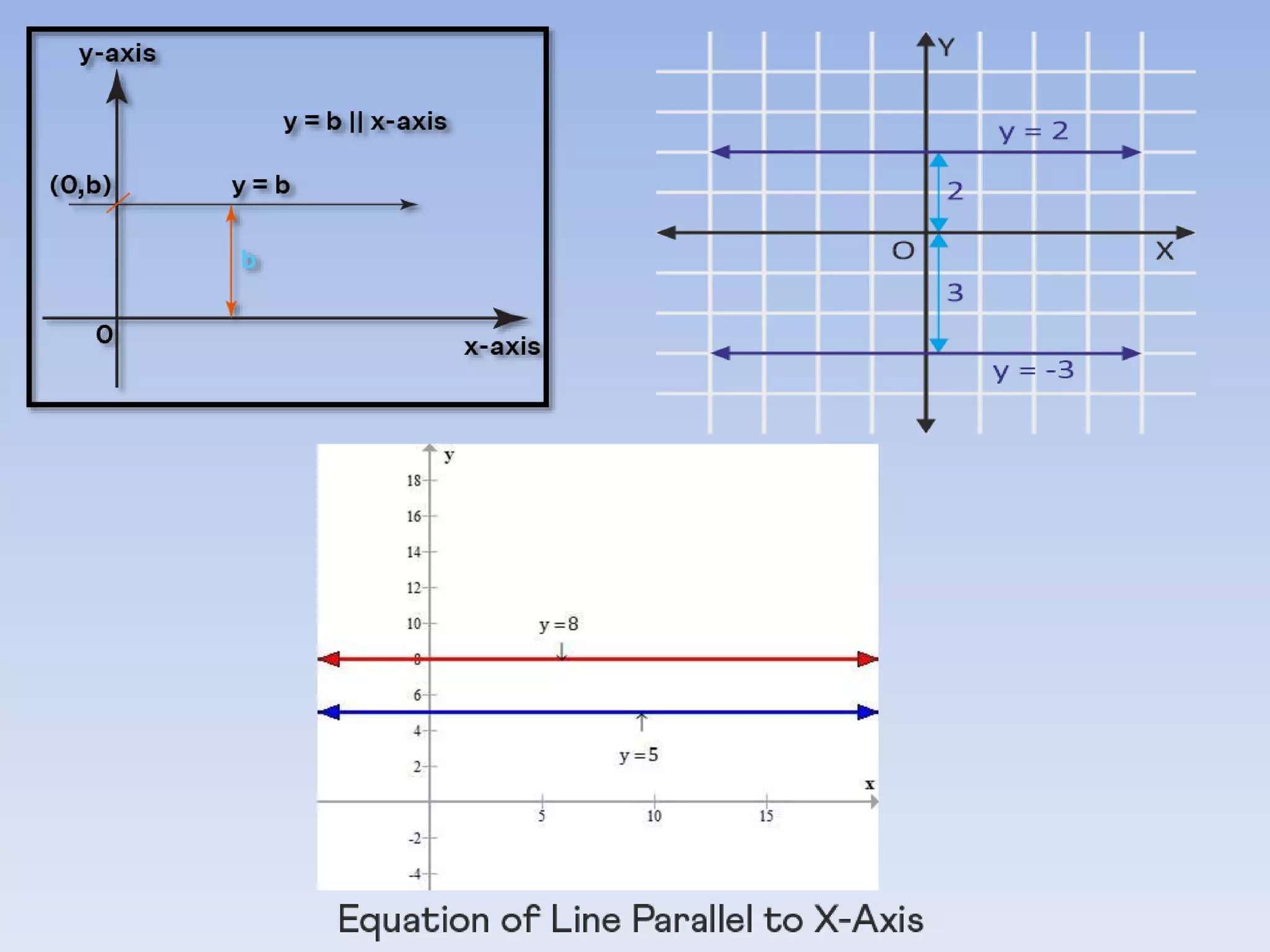
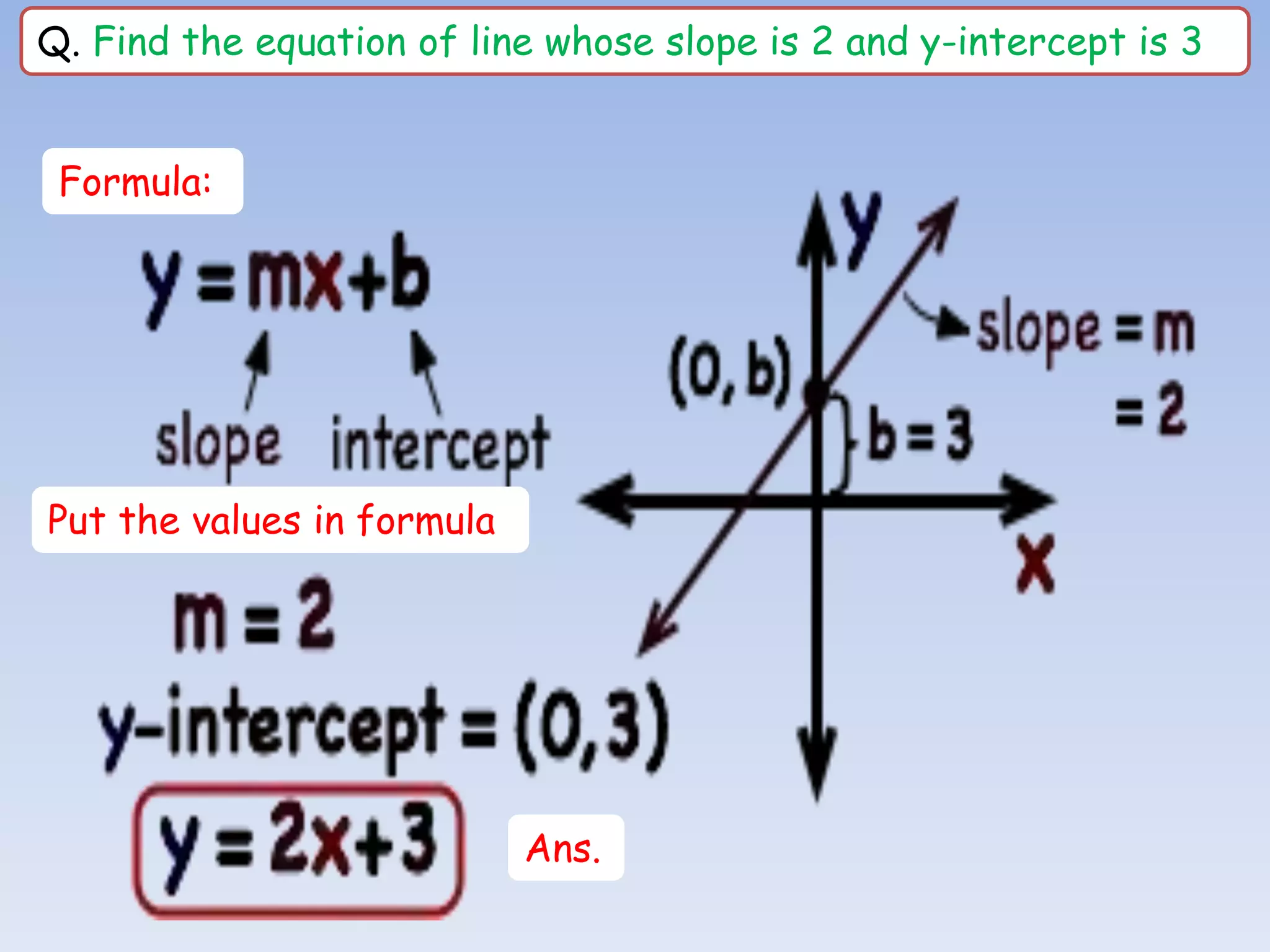
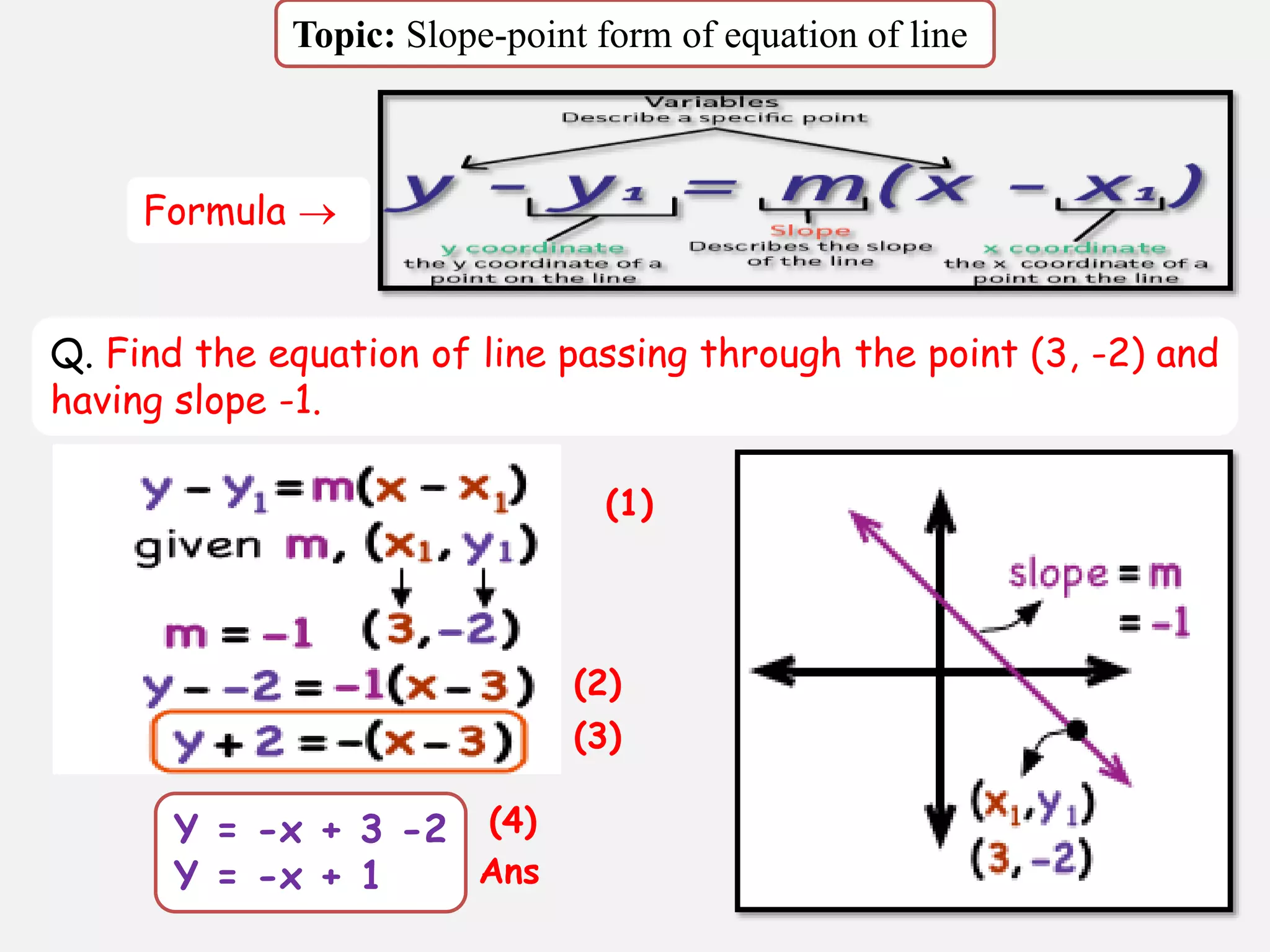
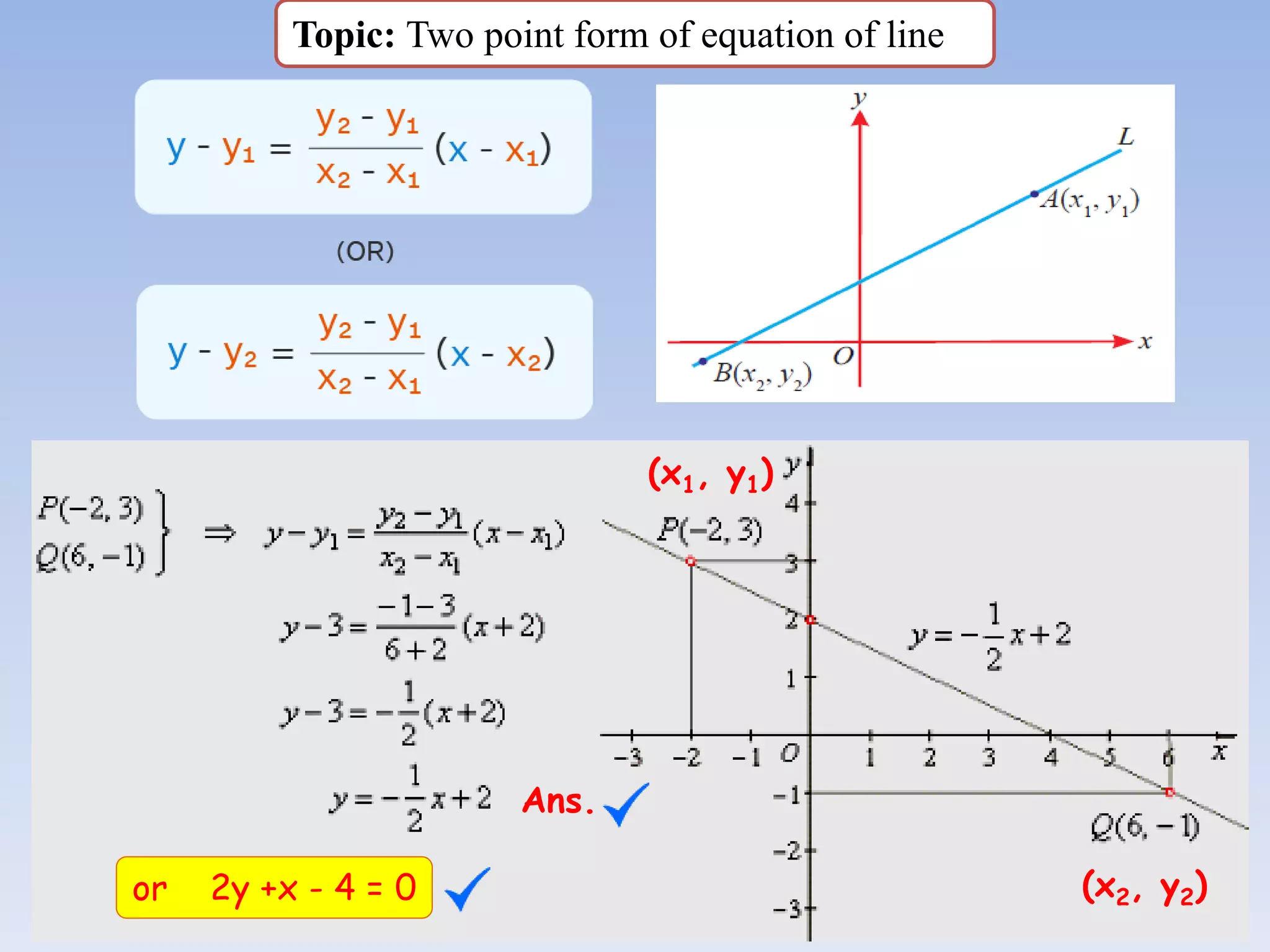
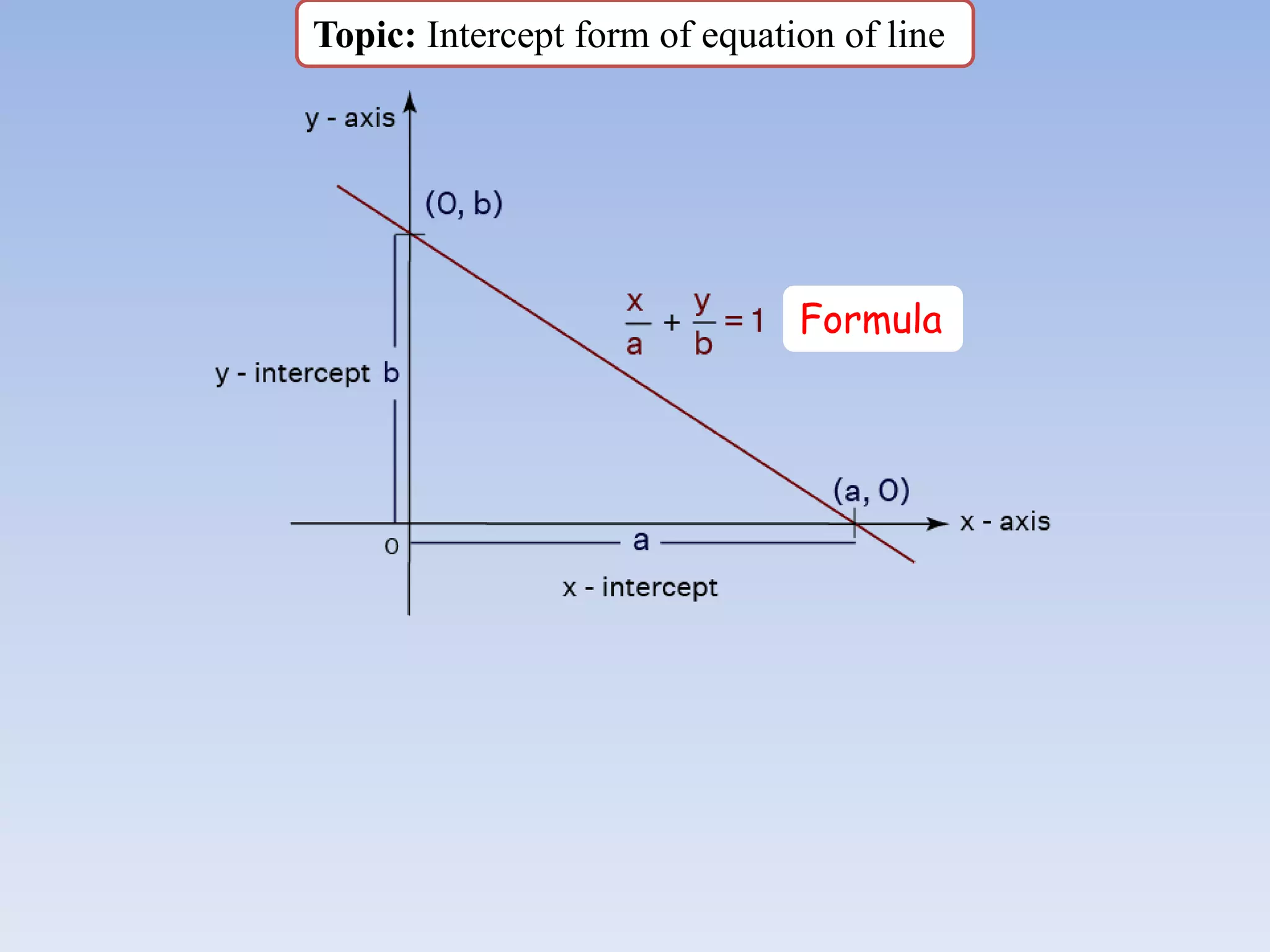
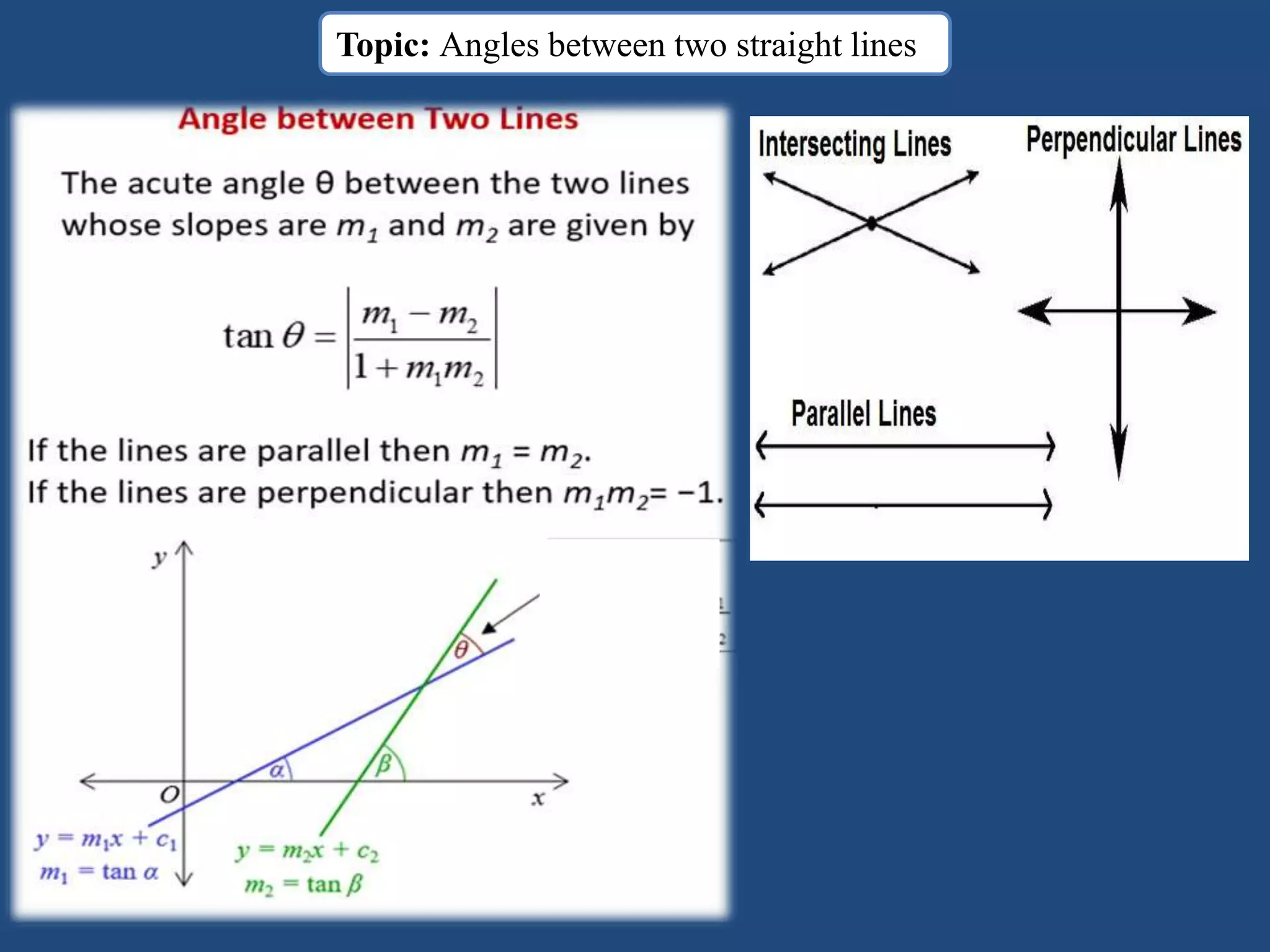
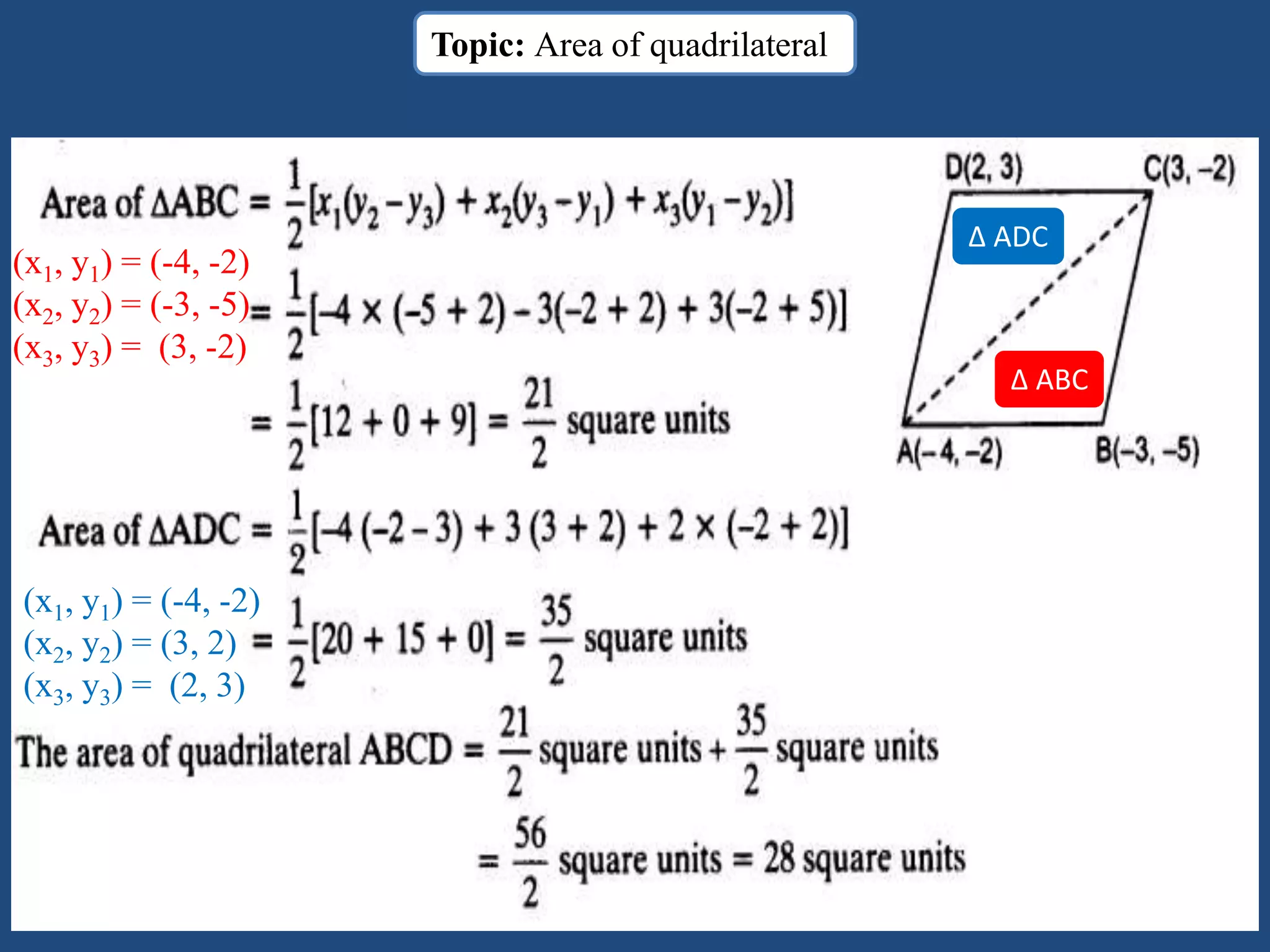
The document provides information about a mathematics course titled "Elementary Mathematics" for first year students. It includes details about the teacher, contact information, and topics that will be covered such as straight lines, coordinate systems, distance and section formulas, forms of equations of lines, and calculating areas of triangles and quadrilaterals. Formulas and examples are provided for finding slopes, intercepts, points of intersection, angles between lines, and applying formulas to find distances, ratios, and areas.

1. Title of the Course: Elementary Mathematics
Class: First Year, First Semester
Teacher:
Dr. Ramkrishna Singh Solanki
Assistant Professor: Mathematics and Statistics
Contact: +919826026464
email: rsolankisolanki_stat@jnkvv.org
College of Agriculture Balaghat
Murjhad Farm, Waraseoni, M.P. 481331

2. Topic: Straight Line
Definition:
• A straight line is an endless one-dimensional figure that has no width.
• A straight line is an infinite length line that does not have any curves on it.
• A straight line is shortest distance between two points.
Straight Line

3. Two dimensional coordinate system
O
(0, 0)
↑
Horizontal Line
← Vertical line
I Quadrant
II Quadrant
III Quadrant
IV Quadrant
= (X1, Y1)
(X3, Y3)
(X2, Y2)

4. Topic: Distance formula
(X1, Y1)
(X2, Y2)
unit

5. unit

6. Distance of a point from the origin

7. Topic: Section formula (Internal division)

8. × × × ×

9. m
n
(X1, Y1)
(X2, Y2)

10. Topic: Section formula (External division)

11. Given : A (x1, y1) = (4, 5) and B (x2, y2) = (7, -1)
P (x, y) divides the line segment externally in the ratio of 4 : 3 i.e m : n = 4 : 3
value of x = (m*x2 – n*x1) / (m – n)
=> (4 * 7 – 3 * 4) / (4 – 3) = 16
value of y = (m*y2 – n*y1) / (m – n )
=> (4 * (-1) – 3 * 5) / (4 – 3) = -19
Hence, the coordinates of P are (16, -19).
P

12. Co-ordinates of mid-point
m
X Y
Example

13. Topic: Change of axes (only origin changed)
k
h
O
(x`, y`)
Original
Shifted
Original
Shifted x = x` + h
y = y` + k
or
x` = x - h
y ` = y - k
Translation of axes

15. Topic: Equation of co-ordinate axes
(x, 0)
A
B
(x, 0)
C = (0, y)

16. Topic: Equation of lines parallel to axes

18. Topic: Slope of a line
Definition: The gradient or slope of a line (not parallel to the axis of y) is the
trigonometrical tangent of the angle (inclination) which the line makes with the
positive direction of the x-axis.
Slope of NM = m = tan α Slope of PQ = m = tan β

20. = Undefined

25. Intercept
A
B
A
B
P
Q O
Note: A horizontal line has no x-intercept and vertical line has no
y-intercept.

26. 1. Slope-Intercept form of equation of line
2. Slope-point form of equation of line
3. Two point form of equation of line
4. Intercept form of equation of line
5. Normal form of equation of line
6. General form of equation of line
Topic: Forms of equation of line

27. Slope-intercept form of equation of line

28. b
Given  (1)
(4)
(2)
(3)
(5)

29. Q. Find the equation of line whose slope is 2 and y-intercept is 3
Formula:
Put the values in formula
Ans.

30. Topic: Slope-point form of equation of line
Formula 
Q. Find the equation of line passing through the point (3, -2) and
having slope -1.
Y = -x + 3 -2
Y = -x + 1
(2)
(1)
(4)
(3)
Ans

31. Formula 
Given 
Q
Ans

32. Topic: Two point form of equation of line
(x1, y1)
(x2, y2)
Ans.
or 2y +x - 4 = 0

33. Topic: Intercept form of equation of line
Formula

34. Q. A line has an x-intercept of 5 and a y-intercept of 3. Find its equation.
Formula
a = 5, b = 3
0
15
3
5
3
5
3
5
3
5
15
3
15
5
15
5
3
1
15
5
3
1
3
5






















X
Y
or
X
Y
X
Y
X
Y
Y
X
Y
X
Y
X
Given 

35. Topic: Normal form of equation of line
α
p

36. Example: Find the equation of the straight line which is at a of distance 7 units from
the origin and the perpendicular from the origin to the line makes an angle 45° with
the positive direction of x-axis.
Solution: We know that the equation of the straight line upon which the length of
the perpendicular from the origin is p and this perpendicular makes an angle α with
x-axis is x cos α + y sin α = p.
Here p = 7 and α = 45°
Therefore, the equation of the straight line in normal form is
x cos 45° + y sin 45° = 7
2
7
2
7
7
2
7
2
2
7
2
1
2
1


















x
y
y
x
y
x
y
x
y
x

39. Topic: Point of intersection of two straight lines
Point of intersection means the point at which two lines intersect. These
two lines are represented by the equation a1x + b1y + c1= 0 and
a2x + b2y + c2 = 0, respectively.
The formula of the point of Intersection of two lines is











1
2
2
1
2
1
1
2
,
1
2
2
1
1
2
2
1
)
,
(
b
a
b
a
c
a
c
a
b
a
b
a
c
b
c
b
y
x

42. y – 4x + 7 = 0
y + 2x - 17 = 0
i
ii

43. Topic: Angles between two straight lines

44. 3x - 2y + 7 = 0
-2y = -3x – 7
y = (-3/-2)x – 7/(-2)
y = (3/2)x + (7/2)
y = mx + c
2y + 4x - 3 = 0
2y = - 4x + 3
y = (- 4/2)x + 3/2
y = ( - 2)x + (3/2)
y = mx + c
4
7
tan 1 
 


45. Topic: Area of triangle
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
1
3
1
3
2
3
2
1
1
3
2
3
2
1
3
2
1
y
y
x
y
y
x
y
y
x
y
y
x
y
y
x
y
y
x
y
y
x
y
y
x
y
y
x
y
y
x
y
y
x
y
y
x

























46. Example: Find the area of the triangle whose vertices are (2, 3); (-1, 0) and (2, -4).

47. (x1, y1) = (-4, -2)
(x2, y2) = (-3, -5)
(x3, y3) = (3, -2)
(x1, y1) = (-4, -2)
(x2, y2) = (3, 2)
(x3, y3) = (2, 3)
Δ ABC
Δ ADC
Topic: Area of quadrilateral