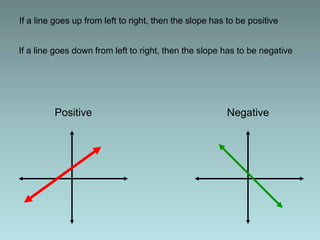
This lecture discusses distance, midpoint, slope, lines, symmetries of graphs, equations of circles, and quadratic equations. It defines distance as the square root of the sum of the squared differences of x- and y-coordinates between two points. The midpoint formula finds the midpoint of a line segment between two points. Slope is defined as the rise over the run between two points on a line. Lines can be written in point-slope form, slope-intercept form, and intercept forms. Parallel and perpendicular lines are identified based on equal or negative reciprocal slopes. Symmetries of graphs include reflections across the x-axis, y-axis, or origin. The equation of a circle is given by (x-h)2

1. Calculus And Analytical
Geometry
MTH-310

2. Lecture 3

3. In this lecture we shall
Distance
Midpoint Formula
Slope
Lines
Symmetries of Graph
Equation of Circle

4. Distance
The distance between to point and is1p 2p
2 2
1 2 2 1 2 1,d p p a a b b

5. Midpoint Formula
The midpoint M of segment is1 2p p
1 2 1 2 1 2
1 1
,
2 2
M p p x x y y

6. Example
Given A(-2,3) and B(4,-2), find:
(a)The distance between A and B
(b) The midpoint M of segment AB

7. Slope
The ratio of vertical change (rise) to horizontal change
(run) of a line.
or
Slope basically describes the steepness of a line
12
12
xx
yy
m

8. Example:
In each part find the slope of the line through

9. If a line goes up from left to right, then the slope has to be positive
If a line goes down from left to right, then the slope has to be negative
Positive Negative

10. Horizontal lines have a slope of zero while vertical lines have no slope
HorizontalVertical
m = 0
m = no
slope

11. INTERCEPTS
An intercept of a line is a point where a line crosses an axis.
The y-intercept is the point at which the line crosses the y-axis.
The x-intercept is the point at which the line crosses the x-axis.

12. Equation of a Straight Line
Point – Slope Form
Slope-Intercept Form

13. Point – Slope Form
Given a point and the slope of a line we can
write the equation of the line in
point – slope form
Given a line passes through point (-3,5) and has a slope of -¾.Write
an equation of the line.
Write the equation of the line that goes through the points (6, –4) and
(2, 8) .

14. Slope-Intercept Form
Slope – Intercept Form:
y = mx + b
m = the slope of the line … b = the y-intercept
EXAMPLE:
WHAT IS AN EQUATION OF THE LINE
1
5
m 0, 3and the y-intercept is
Example: y = 3x – 6

15. Find the equation of lines
0 54321
1
2
3
4
5
-1
-4
-5
-5
-3
-4
-2
-3
-1
-2 x
y
A
B
C
D
E
F
J
K

16. Parallel Lines
Two lines with the same slope are said to be parallel lines. If you
graph them they will never intersect.
We can decide algebraically if two lines are parallel by finding the
slope of each line and seeing if the slopes are equal to each other.
Testing if Lines are Parallel
Are the lines parallel?12 3 9 and -8 2 14x y x y

17. Practice Constructing Parallel Lines
Find the equation of the line going through the point (4,1) and
parallel to 3 7y x
Find the equation of the line going through the point (-2,7) and
parallel to 2 8x y

18. Perpendicular Lines
Perpendicular lines are lines that intersect in a right angle.
We can decide algebraically if two lines are perpendicular by finding the
slope of each line and seeing if the slopes are negative reciprocals of
each other. This is equivalent to multiplying the two slopes together and
seeing if their product is –1.
Testing if Lines Are Perpendicular
1
Are the lines 2 5 and 4 perpendicular?
2
x y y x

19. Constructing Perpendicular Lines
Find the equation of a line going through the point (3, -5) and
perpendicular to 2 8
3
y x
Find the equation of the line going through the point (4,1) and
perpendicular to 3 7y x

20. Quadratic Equation
ax2 + bx + c = 0, where a ≠ 0.
Methods Used to Solve Quadratic Equations
By Factorization
By Completing Square Method
Quadratic Formula

21. Symmetry of Graph
There are three type of symmetry
(1)Symmetry about x-axis
(2)Symmetry about y-axis
(3)Symmetry about origin
2
2
3
1
( )
2
( )
( )4
a y x
b y x
c y x

22. Equation of a Circle
The center of a circle is given by (h, k)
The radius of a circle is given by r
The equation of a circle in standard form is
(x – h)2 + (y – k)2 = r2

23. Example
Find an equation of circle that has center C(-2,3) and
contains the point D(4,5).
Identify the center and radius and sketch the graph:
2534
22
yx
Identify the center and radius and sketch the graph:
6499 22
yx