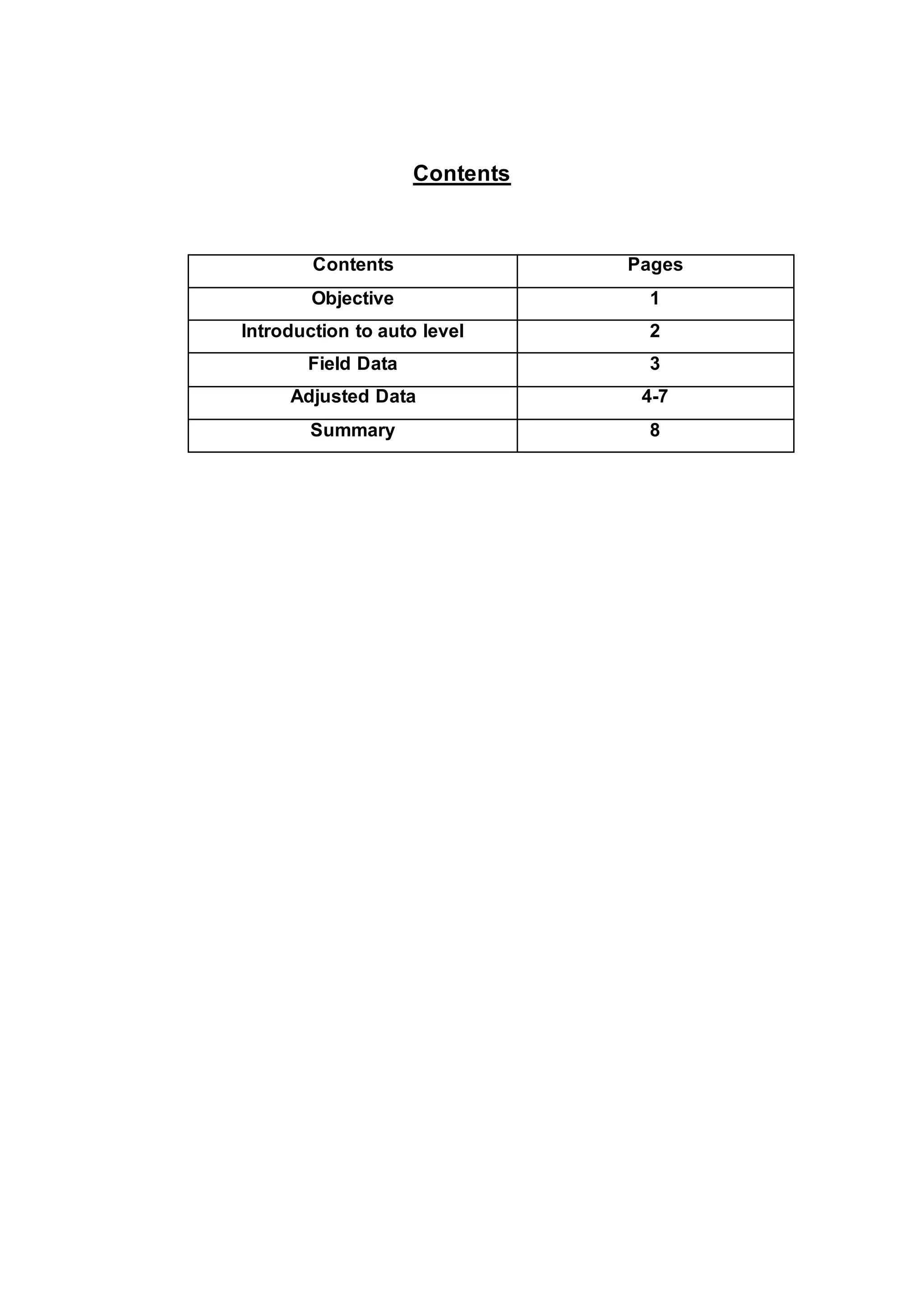
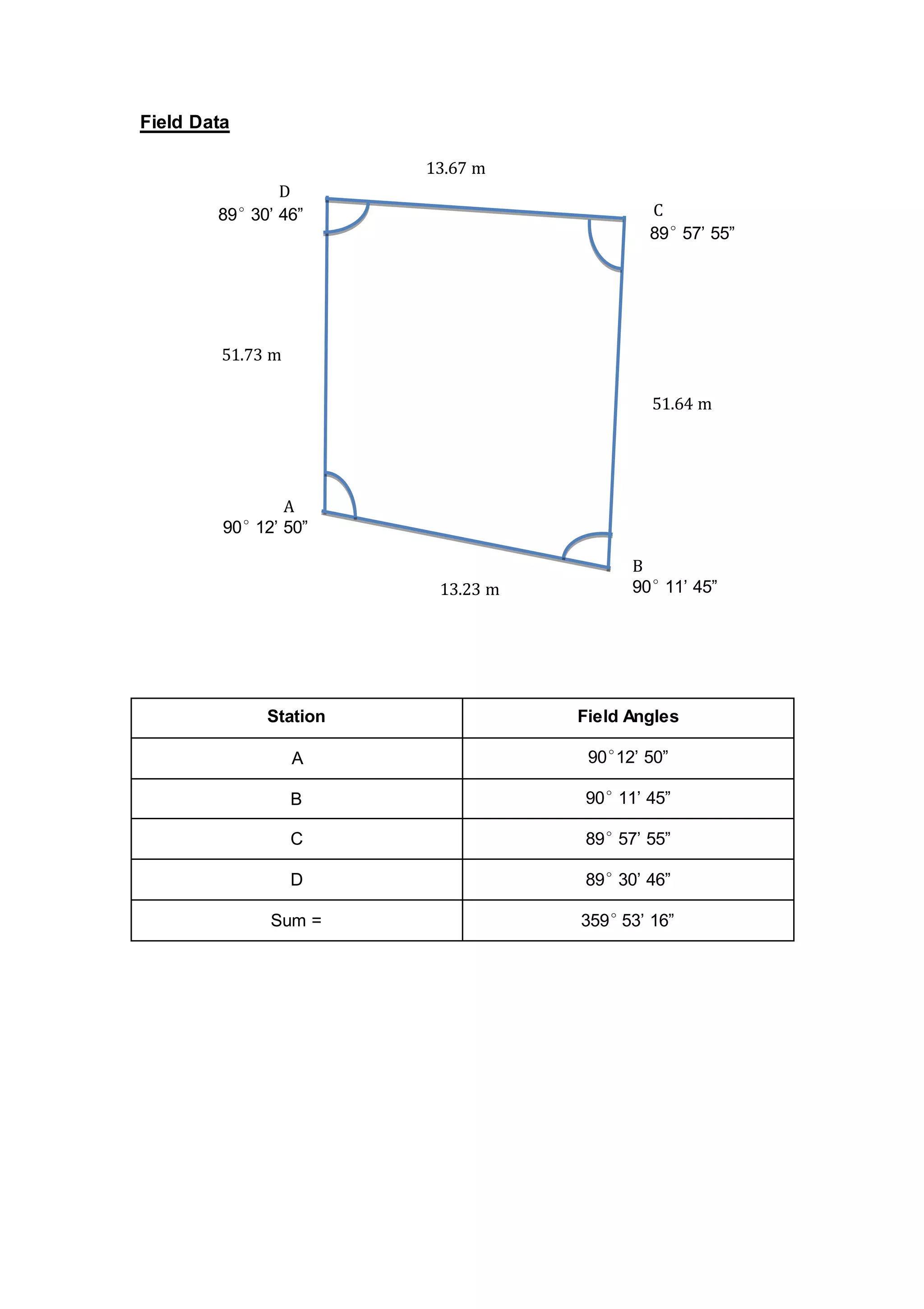
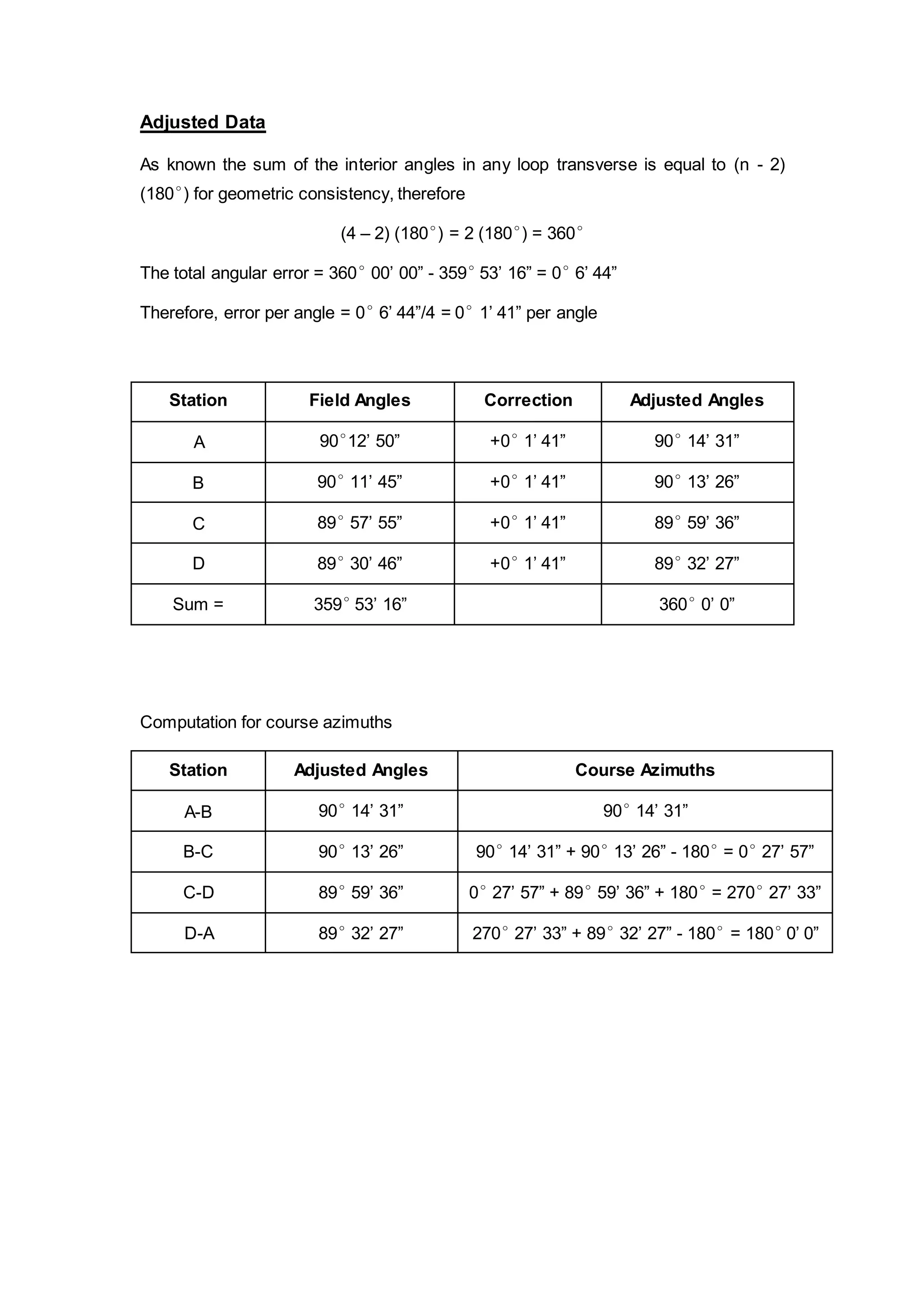
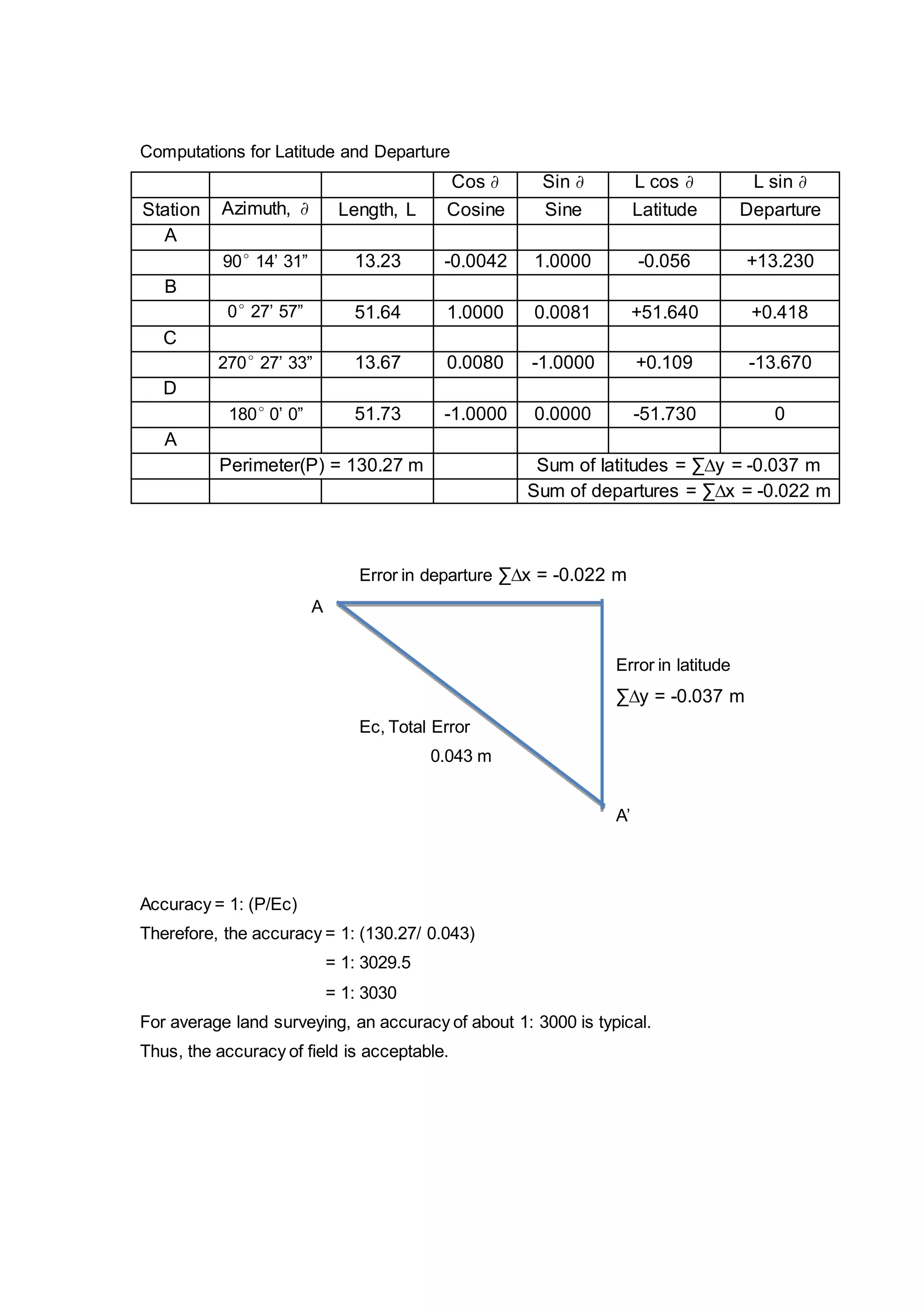
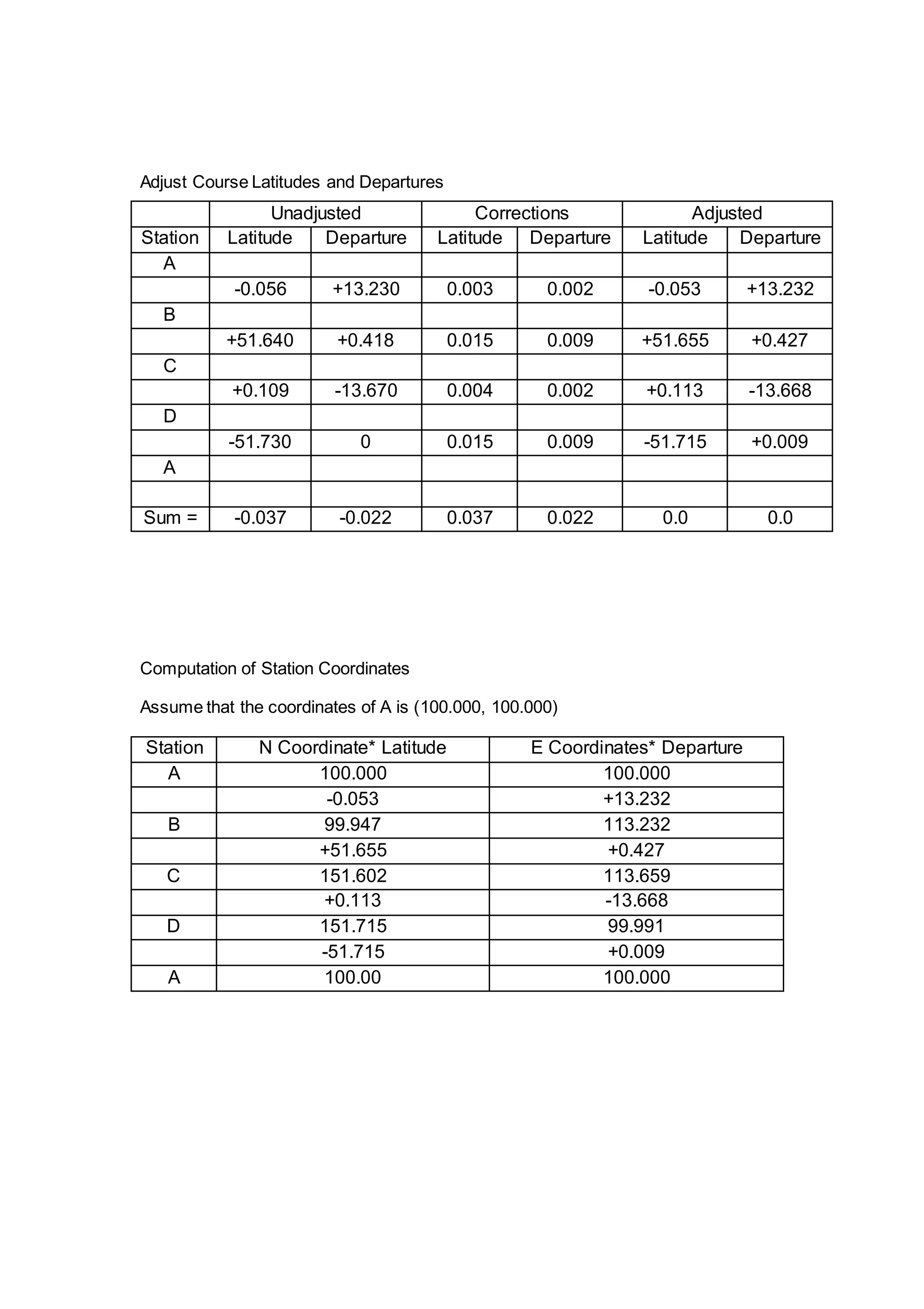
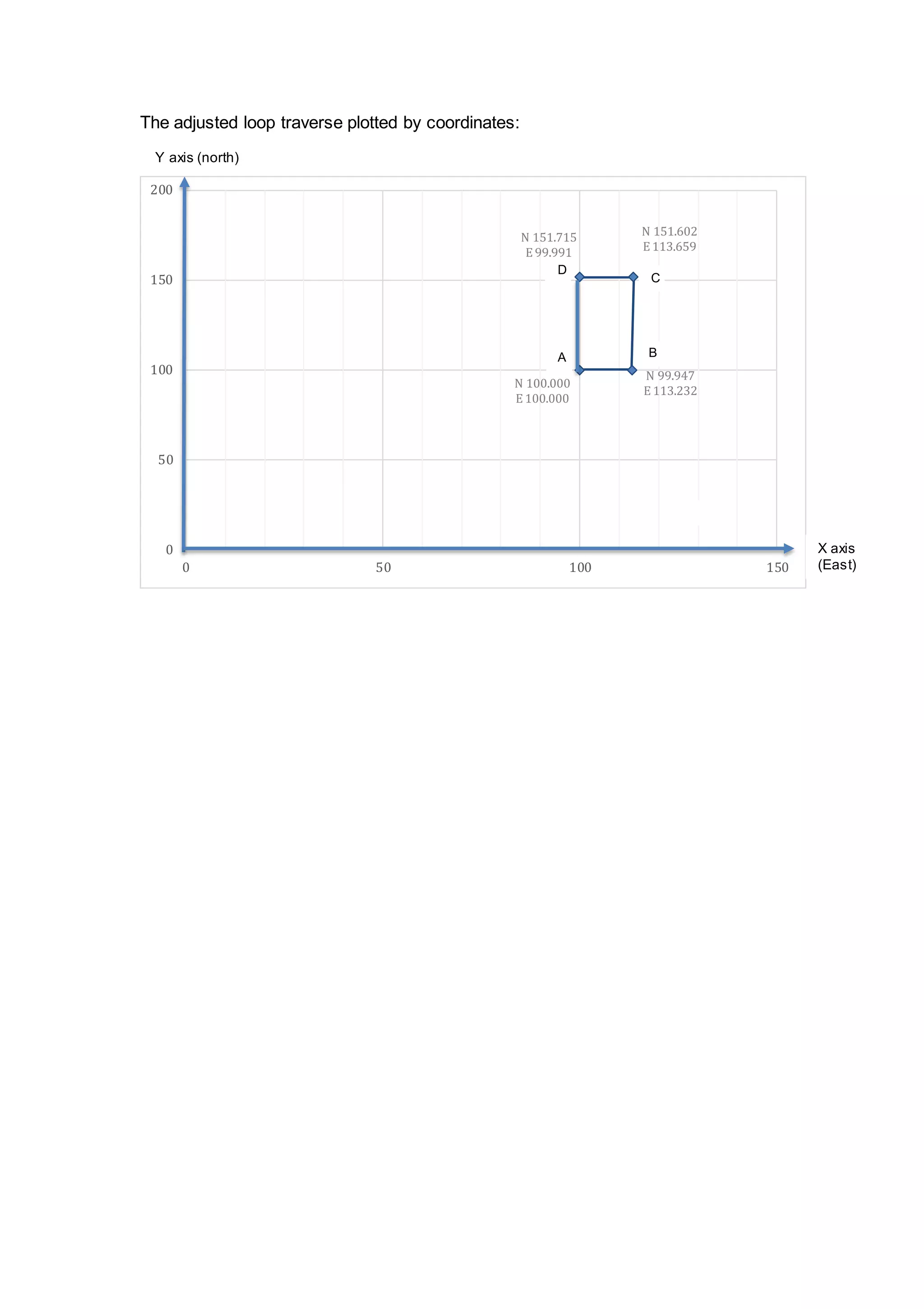
The document describes a student fieldwork assignment using a theodolite to measure horizontal angles between stations A, B, C and D set up in a loop traverse. Field measurements were taken, with a total angular error of 0°6'44". Errors were distributed equally between angles, and adjusted angles and coordinates were calculated. The accuracy of 1:3030 for the adjusted loop was found to be acceptable for average land surveying.

1. SCHOOL OF ARCHITECTURAL,
BUILDING &
DESIGN
BACHELOR OF QUANTITY SURVEYING (HONOURS)
AUGUST 2014
[QSB 60203] SITE SURVEYING
Fieldwork 2
Group Member: Eley Chong Shu Hui 0319458
Melvin Lim 0315772
Moy Chin Hoong 0314014
Muhammad Hakim 0310371
Lecturer : CHAI VOON CHIET

2. Contents
Contents Pages
Objective 1
Introduction to auto level 2
Field Data 3
Adjusted Data 4-7
Summary 8

3. Objectives
 To allow us to have a better understanding or knowledge about the process
of using the instrument (Theodolite) rather than learning from a video in class.
 To enable us to have the experience in using theodolite such as setting up,
collaborating, calculating and recording data.
 To enable us to know the methods to measure horizontal angles between
lines.
 To allow us to learn more about the life being a quantity surveyor.
 To allow us to experience and expose to the actual working environment in
site such as working under the hot weather.
 To allow us to have the teamwork while carrying out the fieldwork.
 To enable us to learn how to analyze the data collected.
 To allow us to understand how to distribute different types of error from the
data collected on field.
 To enable us to have the knowledge in reading the positions on ranging rods.
 To enable us to have a basic knowledge on how to set up the points.
 To allow us to have the ability to undertake the site measurements and
calculations.
 To enable us to know the precautions should be taken while using Theodolite.

4. Introduction to theodolite
A theodolite is a precision instrument for measuring angles in the horizontal and
vertical planes. Theodolites are used mainly for surveying applications, and have
been adapted for specialized purposes in fields like meteorology and rocket
launch technology. A modern theodolite consists of a movable telescope mounted
within two perpendicular axes, the horizontal or trunnion axis, and the vertical axis.
When the telescope is pointed at a target object, the angle of each of these axes can
be measured with great precision, typically to seconds of arc.
Theodolites may be either transit or non-transit. Transit theodolites are those in
which the telescope can be inverted in the vertical plane, whereas the rotation in the
same plane is restricted to a semi-circle for non-transit theodolites. Some types of
transit theodolites do not allow the measurement of vertical angles.
The builder's level is sometimes mistaken for a transit theodolite, but it measures
neither horizontal nor vertical angles. It uses a spirit level to set a telescope level to
define a line of sight along a horizontal plane.
Electronic Theodolite

5. Field Data
D
89° 30’ 46”
A
51.73 m
90° 12’ 50”
C
89° 57’ 55”
51.64 m
B
90° 11’ 45”
13.67 m
13.23 m
Station Field Angles
A 90°12’ 50”
B 90° 11’ 45”
C 89° 57’ 55”
D 89° 30’ 46”
Sum = 359° 53’ 16”

6. Adjusted Data
As known the sum of the interior angles in any loop transverse is equal to (n - 2)
(180°) for geometric consistency, therefore
(4 – 2) (180°) = 2 (180°) = 360°
The total angular error = 360° 00’ 00” - 359° 53’ 16” = 0° 6’ 44”
Therefore, error per angle = 0° 6’ 44”/4 = 0° 1’ 41” per angle
Station Field Angles Correction Adjusted Angles
A 90°12’ 50” +0° 1’ 41” 90° 14’ 31”
B 90° 11’ 45” +0° 1’ 41” 90° 13’ 26”
C 89° 57’ 55” +0° 1’ 41” 89° 59’ 36”
D 89° 30’ 46” +0° 1’ 41” 89° 32’ 27”
Sum = 359° 53’ 16” 360° 0’ 0”
Computation for course azimuths
Station Adjusted Angles Course Azimuths
A-B 90° 14’ 31” 90° 14’ 31”
B-C 90° 13’ 26” 90° 14’ 31” + 90° 13’ 26” - 180° = 0° 27’ 57”
C-D 89° 59’ 36” 0° 27’ 57” + 89° 59’ 36” + 180° = 270° 27’ 33”
D-A 89° 32’ 27” 270° 27’ 33” + 89° 32’ 27” - 180° = 180° 0’ 0”

7. Computations for Latitude and Departure
Cos ∂ Sin ∂ L cos ∂ L sin ∂
Station Azimuth, ∂ Length, L Cosine Sine Latitude Departure
A
90° 14’ 31” 13.23 -0.0042 1.0000 -0.056 +13.230
B
0° 27’ 57” 51.64 1.0000 0.0081 +51.640 +0.418
C
270° 27’ 33” 13.67 0.0080 -1.0000 +0.109 -13.670
D
180° 0’ 0” 51.73 -1.0000 0.0000 -51.730 0
A
Perimeter(P) = 130.27 m Sum of latitudes = ΣΔy = -0.037 m
Sum of departures = ΣΔx = -0.022 m
Error in departure ΣΔx = -0.022 m
A
Error in latitude
ΣΔy = -0.037 m
Ec, Total Error
0.043 m
A’
Accuracy = 1: (P/Ec)
Therefore, the accuracy = 1: (130.27/ 0.043)
= 1: 3029.5
= 1: 3030
For average land surveying, an accuracy of about 1: 3000 is typical.
Thus, the accuracy of field is acceptable.

8. Adjust Course Latitudes and Departures
Unadjusted Corrections Adjusted
Station Latitude Departure Latitude Departure Latitude Departure
A
-0.056 +13.230 0.003 0.002 -0.053 +13.232
B
+51.640 +0.418 0.015 0.009 +51.655 +0.427
C
+0.109 -13.670 0.004 0.002 +0.113 -13.668
D
-51.730 0 0.015 0.009 -51.715 +0.009
A
Sum = -0.037 -0.022 0.037 0.022 0.0 0.0
Computation of Station Coordinates
Assume that the coordinates of A is (100.000, 100.000)
Station N Coordinate* Latitude E Coordinates* Departure
A 100.000 100.000
-0.053 +13.232
B 99.947 113.232
+51.655 +0.427
C 151.602 113.659
+0.113 -13.668
D 151.715 99.991
-51.715 +0.009
A 100.00 100.000

9. The adjusted loop traverse plotted by coordinates:
Y axis (north)
C
D
A B
N 100.000
E 100.000
N 151.602
E 113.659
N 99.947
E 113.232
N 151.715
E 99.991
200
150
100
50
0
0 50 100 150
X axis
(East)

10. Summary
A theodolite is a precision instrument for measuring angles in the horizontal and
vertical planes. Theodolites are used mainly for surveying applications, and have
been adapted for specialized purposes in fields like meteorology and rocket launch
technology. We were assigned to use this instrument for angle calculation. In this
experienced fieldwork, we needed more than 2 hours to complete the angle
calculation. The first thing we did was setting up the instrument. We leveled the
theodolite before we took the measurement. We took extra time to do that because
to stabilize the instrument was a bit hard.
Firstly, the theodolite is placed at station A and need to adjust the theodolite until it is
in horizontal level. Then, the station A, B, C, D must be stated on the site to form a
loop traverse by using the small stones. We use theodolite to measure the angles of
four stations as our field data. During measurement, the vertical and horizontal
angles will be shown on the digital readout panel. Everything went well but the
readings were imperfect so we had to do some distribution error.
Our total angular for the loop traverse is 359° 53’ 16” and the total angular error is
about 0° 6’ 44”, therefore for each angle, it has 0° 1’ 41” error in angle. Before adjust
the readings we get, the accuracy (1:3000) is important to be calculated to ensure
the error of closure and accuracy are acceptable. Fortunately, the accuracy is about
1: 3030 that is a typical accuracy for average land surveying.
The field data is adjusted and the coordinates of four stations are stated at the graph
with assuming the coordinates of station A is (100.000, 100.000).