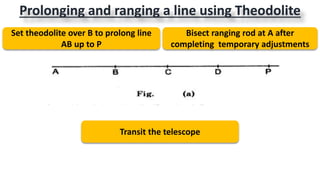
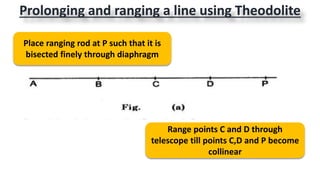
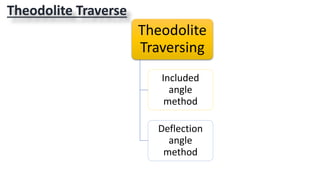
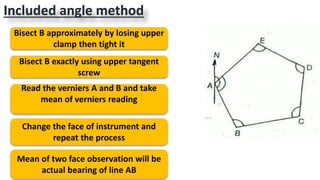
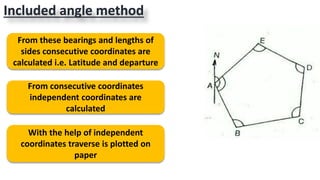
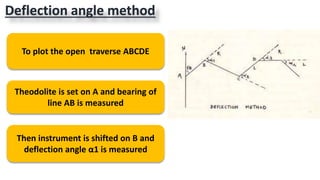
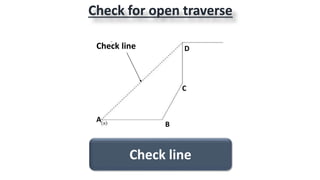
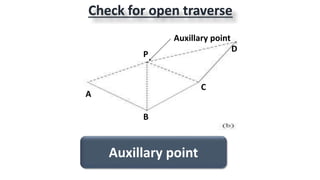
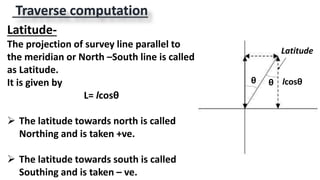
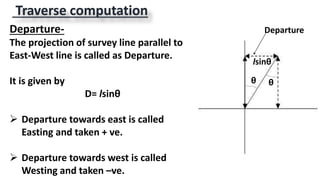
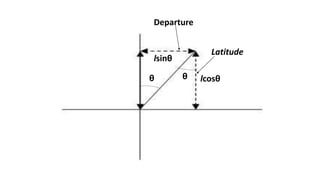
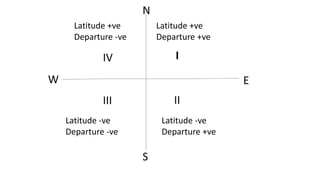
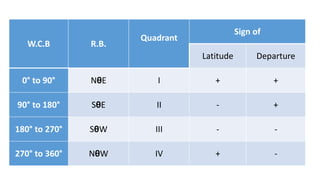
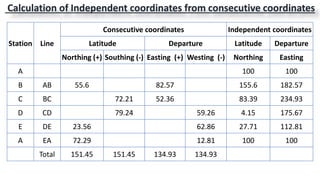
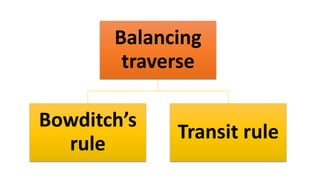
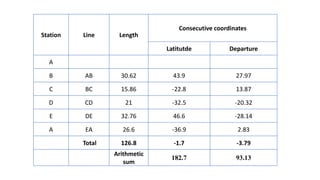
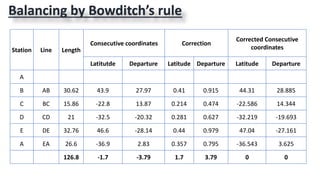
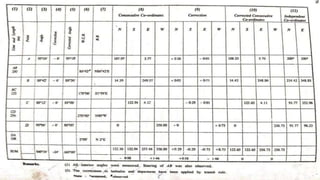
This document provides information on theodolite surveying. It discusses how to measure the magnetic bearing of a line, prolong and range a line, measure deflection angles, vertical angles, and includes steps for closed and open traverse surveys using the included angle and deflection angle methods. It also covers topics like observation tables, consecutive and independent coordinates, and balancing a traverse using Bowditch's rule and the transit rule.

1. 2.THEODOLITE SURVEYING
(Part 2)
By
Mr. Naufil Sayyad

2. Measurement of magnetic bearing of line
Set theodolite over O and complete
temporary adjustments
Attach trough compass to theodolite
beside telescope
Release the needle of trough compass
Turn the telescope by loosing lower
clamp till needle directs the North
approximately
Tight the lower clamp

3. Measurement of magnetic bearing of line
Use lower tangent screw to make
telescope to sight exact North
Turn telescope towards A by loosing
upper clamp and bisect A
approximately
Tight the upper clamp
Bisect A finely by using upper tangent
screw

4. Measurement of magnetic bearing of line
Read both verniers and take mean of
Vernier angle
Change the face of instrument and
repeat the process
Mean angle of two observation is
actual magnetic bearing of line OA

5. Prolonging and ranging a line using Theodolite
Set theodolite over B to prolong line
AB up to P
Bisect ranging rod at A after
completing temporary adjustments
Transit the telescope

6. Prolonging and ranging a line using Theodolite
Place ranging rod at P such that it is
bisected finely through diaphragm
Range points C and D through
telescope till points C,D and P become
collinear

7. Deflection angle
Deflection angle is an angle
made by survey line with
prolongation of preceding
line.Angle Φ in figure is
deflection angle.
Φ

8. Measurement of Deflection angle using Theodolite
To measure deflection angle
Set theodolite over B and bisect A
Transit the telescope
Bisect C by loosing upper clamp
Bisect C finely using upper tangent
screw and take Vernier readings
Φ
Φ

9. Measurement of Deflection angle using Theodolite
Change the face of instrument and
repeat the process
Mean of two observations will be
actual Deflection angle
Φ
Φ

10. Vertical angle
Q
RO
The angle measured in vertical
plane is called as Vertical angle.
The vertical angle measured
below line of collimation is called
as ‘Angle of Depression’ and that
of above line of collimation is
called ‘Angle of Elevation’.
Angle of Elevation
Angle of Depression

11. Measurement of Vertical angle using Theodolite
To measure vertical angle POR
Set theodolite over O
Level the instrument using foot
screws with respect to altitude bubble
Make zero of verniers C and D
approximately coincide to zero of
vertical circle by losing vertical clamp
RO

13. Measurement of Vertical angle using Theodolite
Set verniers C and D to zero exactly
using vertical tangent screw
Now line of collimation is horizontal
Bisect P approximately by losing
vertical clamp then tight it
Using vertical tangent screw bisect P
finely
Read verniers C and D
RO

14. Measurement of Vertical angle using Theodolite
Change the face of instrument and
repeat the process
Mean of two face readings is exact
angle POR
RO

15. Observation table
StationObject Face Angle
Reading on vernier
Mean
angle of
vernier
Mean angle of
observation
RemarkWindow
C
Diff
Window
D
Diff
O
R
Left POR
0°0'0" 15°0'20
"
0°0'0" 15°0'40
"
15°0'30
"
15°0'20"
Angle of
elevatio
n
P 15°0'20" 15°0'40"
O
R
Right POR
0°0'0" 15°0'20
"
0°0'0"
15°0'0"
15°0'10
"P 15°0'20" 15°0'0"

16. Theodolite Traverse
Theodolite
Traversing
Included
angle
method
Deflection
angle
method

17. Included angle method
Set theodolite on station A and carry
out all temporary adjustments
Set verniers A and B at 0° and 180 °
Set trough compass beside telescope
and lose its needle
Turn the telescope till it sights north
approximately by losing lower clamp
Sight north finely using lower tangent
screw

18. Included angle method
Bisect B approximately by losing upper
clamp then tight it
Bisect B exactly using upper tangent
screw
Read the verniers A and B and take
mean of verniers reading
Change the face of instrument and
repeat the process
Mean of two face observation will be
actual bearing of line AB

19. Included angle method
Set theodolite over station B
Measure <ABC by direct method
Similarly from station C,D and E <C,<D
and <E are measured
From included angles and bearing of
first line bearing of all lines is
obtained

20. Included angle method
From consecutive coordinates
independent coordinates are
calculated
With the help of independent
coordinates traverse is plotted on
paper
From these bearings and lengths of
sides consecutive coordinates are
calculated i.e. Latitude and departure

21. Deflection angle method
Theodolite is set on A and bearing of
line AB is measured
Then instrument is shifted on B and
deflection angle α1 is measured
To plot the open traverse ABCDE

22. Deflection angle method
Right hand deflection is taken as
positive
Left hand deflection is taken as
negative
Similarly by setting instrument on C,D
and E deflection angles α2, α3 and α4
are measured

23. Deflection angle method
Lengths of all sides are measured
From bearing of first line and
deflection angles α 1,α2, α3 and α4
bearings of remaining lines are
obtained

24. Sum of measured included angles should be equal to (2n-4)×90°
Sum of measured exterior angles should be equal to (2n+4)×90°
Algebric sum of latitudes should be zero i.e. algebraic sum of
northing should equal to southing.
Check for closed traverse
Closed traverse by included angle method

25. Algebric sum of departures should be zero i.e. algebraic
sum of easting should equal to westing .
Checking length of line from both end Eg. from station A
to B and then from station B to A .
Check for closed traverse
Closed traverse by included angle method

26. Check for closed traverse
Closed traverse by deflection angle method
The algebraic sum of deflection angles should be equal to
360° considering right hand deflection angles as +ve & left
hand deflection angles as –ve.

27. Check for open traverse
Check line
A
B
C
DCheck line

28. Check for open traverse
Auxillary point
A
P
B
C
D
Auxillary point

29. Traverse computation
Latitude-
The projection of survey line parallel to
the meridian or North –South line is called
as Latitude.
It is given by
L= lcosθ
 The latitude towards north is called
Northing and is taken +ve.
 The latitude towards south is called
Southing and is taken – ve.
lcosθθ θ
Latitude

30. Traverse computation
θ θ
Departure-
The projection of survey line parallel to
East-West line is called as Departure.
It is given by
D= lsinθ
 Departure towards east is called
Easting and taken + ve.
 Departure towards west is called
Westing and taken –ve.
lsinθ
Departure

31. θ θ
lsinθ
Departure
lcosθ
Latitude

32. Latitude +ve
Departure +ve
Latitude -ve
Departure +ve
Latitude -ve
Departure -ve
Latitude +ve
Departure -ve
IIV
III II
N
S
W E

33. W.C.B R.B.
Quadrant
Sign of
Latitude Departure
0° to 90° NθE I + +
90° to 180° SθE II - +
180° to 270° SθW III - -
270° to 360° NθW IV + -

34. Consecutive coordinates
 The coordinates of any point when measured with respect to
previous point are called as Consecutive Co ordinates .
 By using this coordinates the traverse is plotted with respect to
previous point
 Coordinates of any point may not be obtained by adding
algebraically latitude and departure of the line.

35. Independent coordinates
 The coordinates of any point when measured with respect to
common origin are called as Independent Co ordinates
 This method of coordinates is better than consecutive ordinates
 By using this coordinates the traverse is plotted with respect to
parallel and perpendicular to meridian.
 Coordinates of any point may be obtained by adding
algebraically latitude and departure of the line.

36. Station Line
Consecutive coordinates Independent coordinates
Latitude Departure Latitude Departure
Northing (+) Southing (-) Easting (+) Westing (-) Northing Easting
A 100 100
B AB 55.6 82.57 155.6 182.57
C BC 72.21 52.36 83.39 234.93
D CD 79.24 59.26 4.15 175.67
E DE 23.56 62.86 27.71 112.81
A EA 72.29 12.81 100 100
Total 151.45 151.45 134.93 134.93
Calculation of Independent coordinates from consecutive coordinates

37. The term balancing is generally applied to the
operation of applying corrections to latitudes and
departures so that algebraic sum of latitudes and
that of departures will be zero. This applies only
when the survey forms a closed polygon.
Balancing the traverse

38. Balancing
traverse
Bowditch’s
rule
Transit rule

39. Bowditch’s rule
The basis of this method is on the assumptions that the
errors in linear measurements are proportional to the length
of the line
 The rule, also termed as the compass rule, is used to
balance the traverse when the angular and linear
measurements are equally precise.
 By this rule, the total error in latitude and in departure is
distributed in proportion to the lengths of the sides.

40. Bowditch’s rule
This rule is most commonly used in traverse adjustment.
Correction to latitude = total error in latitude x ( length of
that side/ perimeter of traverse ).
 Correction to departure = total error in departure x ( length
of that side/ perimeter of traverse )
 If error is negative then correction is positive and vice versa.
6) After applying correction summation all latitudes and
departures must be zero.

41. Transit rule
 The transit rule may be employed where angular
measurements are more precise than the linear
measurements.
 According to this rule, the total error in latitudes and in
departures is distributed in proportion to the latitudes and
departures of the sides.
 It is claimed that the angles are less affected by
corrections applied by transit method than by those by
Bowditch's method.

42. Transit rule
The transit rule is
Correction to latitude of any side
= Total error in latitude ×Latitude of that side/ Arithmetic
sum of Latitudes
Correction to departure of any side
= Total error in departure × Departure of that side/
Arithmetic sum of Departures

43. Station Line Length
Consecutive coordinates
Latitutde Departure
A
B AB 30.62 43.9 27.97
C BC 15.86 -22.8 13.87
D CD 21 -32.5 -20.32
E DE 32.76 46.6 -28.14
A EA 26.6 -36.9 2.83
Total 126.8 -1.7 -3.79
Arithmetic
sum
182.7 93.13

44. By Bowditch’s rule
Correction to latitude of line AB
= total error in latitude x ( length of that side AB/ perimeter of
traverse )
= 1.7 x (30.62/126.84)
=0.41m
Correction to departure of line AB
= total error in departure x ( length of that side AB/ perimeter of
traverse )
= 3.79 x (30.62/126.84)
= 0.915m

45. By Transit rule
Correction to latitude of any side
= Total error in latitude ×Latitude of that side/ Arithmetic sum of
Latitudes
=1.7 x (43.9/182.7)
=0.41m
Correction to departure of any side
= Total error in departure × Departure of that side/ Arithmetic sum
of Departures
= 3.79 x (27.97/93.13)
=1.14m

46. Station Line Length
Consecutive coordinates Correction
Corrected Consecutive
coordinates
Latitutde Departure Latitude Departure Latitude Departure
A
B AB 30.62 43.9 27.97 0.41 0.915 44.31 28.885
C BC 15.86 -22.8 13.87 0.214 0.474 -22.586 14.344
D CD 21 -32.5 -20.32 0.281 0.627 -32.219 -19.693
E DE 32.76 46.6 -28.14 0.44 0.979 47.04 -27.161
A EA 26.6 -36.9 2.83 0.357 0.795 -36.543 3.625
126.8 -1.7 -3.79 1.7 3.79 0 0
Balancing by Bowditch’s rule

47. Gale’s Traverse table