The document summarizes a fieldwork report on traversing. It includes an introduction to closed and open traverses, station selection criteria, and apparatus used including a theodolite, tripod, plumb bob, ranging rods and tape measure. Field data is presented showing the measured angles. Angular errors are calculated and angle adjustments made. Course bearings, azimuths, latitudes and departures are determined. The traverse is checked for accuracy and found acceptable. Latitude and departure corrections are applied using the compass rule. Adjusted station coordinates are presented in a table.

1. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
1 | Page
SCHOOL OF ARCHITECTURE, BUILDING AND
DESIGN
BACHELOR OF QUANTITY SURVEYING (HONOURS)
QSB 60103 - SITE SURVEYING
Fieldwork 2 Report
Traversing
Name Student ID Marks
SHARON CHOW CI YUNG 0313387
TAN CHUU YEE 0315097
MUHAMMAD HAZIQ BIN HAJI
ABD ZARIFUL
0314131
PARHAM FARHADPOOR 0313698

2. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
2 | Page
Table of Contents
Content Page
Cover Page 1
Table of Content 2
1.0 Introduction to Traversing 3
1.1 Closed Traverse 3
1.2 Open Traverse 4
1.3 Station Selection 4
1.4 Azimuth 5
1.5 Bearing 5
1.6 Acceptable Misclosure 6
2.0 Outline of Apparatus 7
2.1 Theodolite 7
2.2 Tripod 8
2.3 Plumb Bob 8
2.4 Ranging Rod 9
2.5 Tape-Measure 9
3.0 Objectives 10
4.0 Field Data 11
4.1 Angular Error & Angle Adjustments 12
4.2 Course Bearings & Azimuths 13
4.3 Course Latitude & Departure 14
5.0 Adjusted Latitude & Departure 15
6.0 Table and Graph of Station Coordinates 16-17
7.0 Summary 18
8.0 References 19

3. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
3 | Page
1.0 Introduction to Traversing
Traversing is one of the traditional methods of carrying out a control survey in plan. Stations
are set out to define a series of traverse lines or legs, the plan length of which can be
measured as can the angles between pairs of line at each station (Muskett, 1995).
There are two types of traverse:
1.1 Closed Traverse
Closed Traverses provide a check on the validity and accuracy of field measurements.
There are two types of closed traverse which are the loop traverse and connecting traverse.
Loop traverse starts and ends at the same point, forming a polygon. Loop traverse is
suitable for many engineering surveys.
Figure 1.0 Loop Traverse
Source:
http://files.carlsonsw.com/mirror/manuals/SightSurvey_2009/scr/Section%2011%20-
%20Tools%20Menu/images/CG_Editor/cge001.png
On the other hand, connecting traverse is similar to open traverse, the only difference is it
begins and end at point of known position at each end of traverse.
Figure 1.1 Loop Traverse
Source: http://www.tpub.com/engbas/13.htm3.gif

4. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
4 | Page
1.2 Open Traverse
Open Traverses are a series of measured straight lines and angles that do not close
geometrically and provide no check and are not recommended. They are usually being
applied in underground surveys.
Figure 1.2 Open Traverse
Source: http://www.tpub.com/engbas/13.htm3.gif
1.3 Station Selection
The stations should be marked out firmly and clearly as well as strongly referenced. The
following are the requirements for the selection of traversing stations (Muskett, 1995):
i) The stations should form a traverse of suitable shape.
ii) Only neighbouring stations along traverse lines need be intervisible.
iii) Where traverse legs are to be taped, the ground should be accessible.
iv) Traverse legs should be approximately equal in length.
v) Existing stations and reference objects should be incorporated.

5. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
5 | Page
1.4 Azimuth
An azimuth is an angle between 0° and 360° measured clockwise from North (Penn State
College of Earth and Mineral Sciences, 2014).
1.5 Bearing
A bearing is an angle less than 90° within a quadrant defined by the cardinal directions (Penn
State College of Earth and Mineral Sciences, 2014).
Figure 1.3 Azimuth and Bearing
Source: https://www.e-
education.psu.edu/geog160/files/geog160/image/Chapter05/Azimuths_Bearings.png

6. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
6 | Page
1.6 Acceptable Misclosure
Generally for land surveying, an accuracy of 1:3000 is typical. The range of acceptable
misclosure can be calculated with the following formula:
Accuracy= 1: (P/Ec)
P= Perimeter of the Entire Traverse
Ec= The Total Error
Table 1.0 Traverse Specification in United States of America.
Source: Federal Control Committee, United States (1974).
Classification First Order Class I (Second
Order)
Class II (Second
Order)
Class I (Third
Order)
Class II (Third
Order)
Recommended
spacing of
principal
stations.
Network
stations 10 to
15 km other
surveys
seldom less
than 3 km.
Principal stations
seldom less than
4km, except in
metropolitan area
surveys, where
the limitation is
0.3km.
Principal stations
seldom less than
2km, except in
metropolitan area
surveys where the
limitation is 0.2km.
Seldom less
than 0.1 km in
tertiary surveys
in metropolitan
area surveys; as
required for
other surveys.
Seldom less
than 0.1 km in
tertiary surveys
in metropolitan
area surveys; as
required for
other surveys.
Position closure
After azimuth
adjustment.
0.04m √k or
1: 100,000
0.08m √k or
1:50,000
0.08 m √k or
1:20,000
0.2m √k or
1: 10,000
0.8m √k or
1:5000

7. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
7 | Page
2.0 Outline of Apparatus
2.1 Theodolite
The basic instrument for setting out lines and angles over wide distances. The original
theodolite was a purely optical instrument, but nowadays most theodolites come with an
electronic distance-measuring attachment commonly known as the EDM (Food and
Agriculture Organization of the United Nations, n.d.).
Figure 2.0 Theodolite
Source: http://www.vpcivil.co.in/wp-content/uploads/2012/08/Topcon-Dt-200-Digital-
Theodolite.jpg

8. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
8 | Page
2.2 Tripod
The tripod is used solely for setting up the theodolite or the level (Food and Agriculture
Organization of the United Nations, n.d.).
Figure 2.1 Tripod
Source: http://www.ysf.com.hk/images/SJA50%20Aluminum%20Tripod-1-c.jpg
2.3 Plumb Bob
The plumb bob or plumb line employs the law of gravity to establish what is “plumb” (that is,
what is exactly vertical, or true). In a sense, the plumb bob is the vertical equivalent of the
line level (Bob Vila, 2014).
Figure 2.2 Plumb Bob
Source: http://www.archtools.eu/images/detailed/0/plumbbob.jpg

9. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
9 | Page
2.4 Ranging Rod
Ranging rods are coloured poles used in tracing out lines on the ground.
Ranging rods can either be purchased outright or made from pieces of straight pipe, roughly
1.5 m long, with red and white bands (150 mm wide) painted as shown in Figure 2.3.
Figure 2.3 Ranging Rod
Source: http://www.nsscanada.com/Images/Prism_Poles/CST001quickrelease.jpg
2.5 Tape-Measure
Fibre or plastic tape-measures typically come in lengths of 20, 30, 50 or 100 m (Food and
Agriculture Organization of the United Nations, n.d.).
Figure 2.4 Fiberglass Tape-Measure
Source:
http://i01.i.aliimg.com/img/pb/585/870/210/1234350266708_hz_myalibaba_web7_1249.jpg

10. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
10 | Page
3.0 Objectives
• To enhance the students’ knowledge in the traversing procedure.
• To enable students to get hands-on experience in setting up and working with the
theodolite.
• To determine the error of misclosure in order to determine whether the traversing is
acceptable or not.
• To allow students to apply the theories that had been taught in the classes in a
hands- on situation such as making adjustments for each angle as well as the
latitude and departure of every single staff station in order to obtain the most
accurate results.

11. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
11 | Page
4.0 Field Data
Station Field Angles
A 73° 47’ 30’’
B 107° 35’ 20’’
C 72° 23’ 00’’
D 106° 12’ 00’’
Sum= 358° 117’ 50’’
359° 57’ 50’’
(not to scale)

12. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
12 | Page
4.1 Angular Error & Angle Adjustments
(4-2)(180°)= 2(180°)= 360°, the sum of interior angles of the traverse must be
360°
Total angular error = 359°57’50’’- 360° = 0° 2’ 10’’
Therefore, error per angle = 0° 2’ 10’’÷5 = 130’’÷5 = 32.5’’ per angle
Station Field Angles Correction Adjusted Angles
A 73° 47’ 30’’ +32.5’’ 73° 48’ 2.5’’
B 107° 35’ 20’’ +32.5’’ 107° 35’ 52.5’’
C 72° 23’ 00’’ +32.5’’ 72° 23’ 32.5"
D 106° 12’ 00’’ +32.5’’ 106° 12’ 32.5’’
Sum= 358° 117’ 50’’ 360° 00’ 00’’
359° 57’ 50’’

13. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
13 | Page
4.2 Course Bearing & Azimuth
73° 48’ 2.5’’ N73° 48’ 2.5’’E
S0°00’00’’E180°00’00’’
N73°47’32.5’’E252°47’27.5’’
252°47’27.5’’
-180°00’00’’
73°47’32.5’’
180°00’00’’
+1°23’55’’
+72°23’32’5"
252°47’27.5’’
1°23’55’’
180°00’00’’
+107° 35’ 52.5’’
+73° 48’ 2.5’’
361°23’55’’
-360°00’00’’
1°23’55’’
N1°23’55’’E
Azimuth N Bearing

14. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
14 | Page
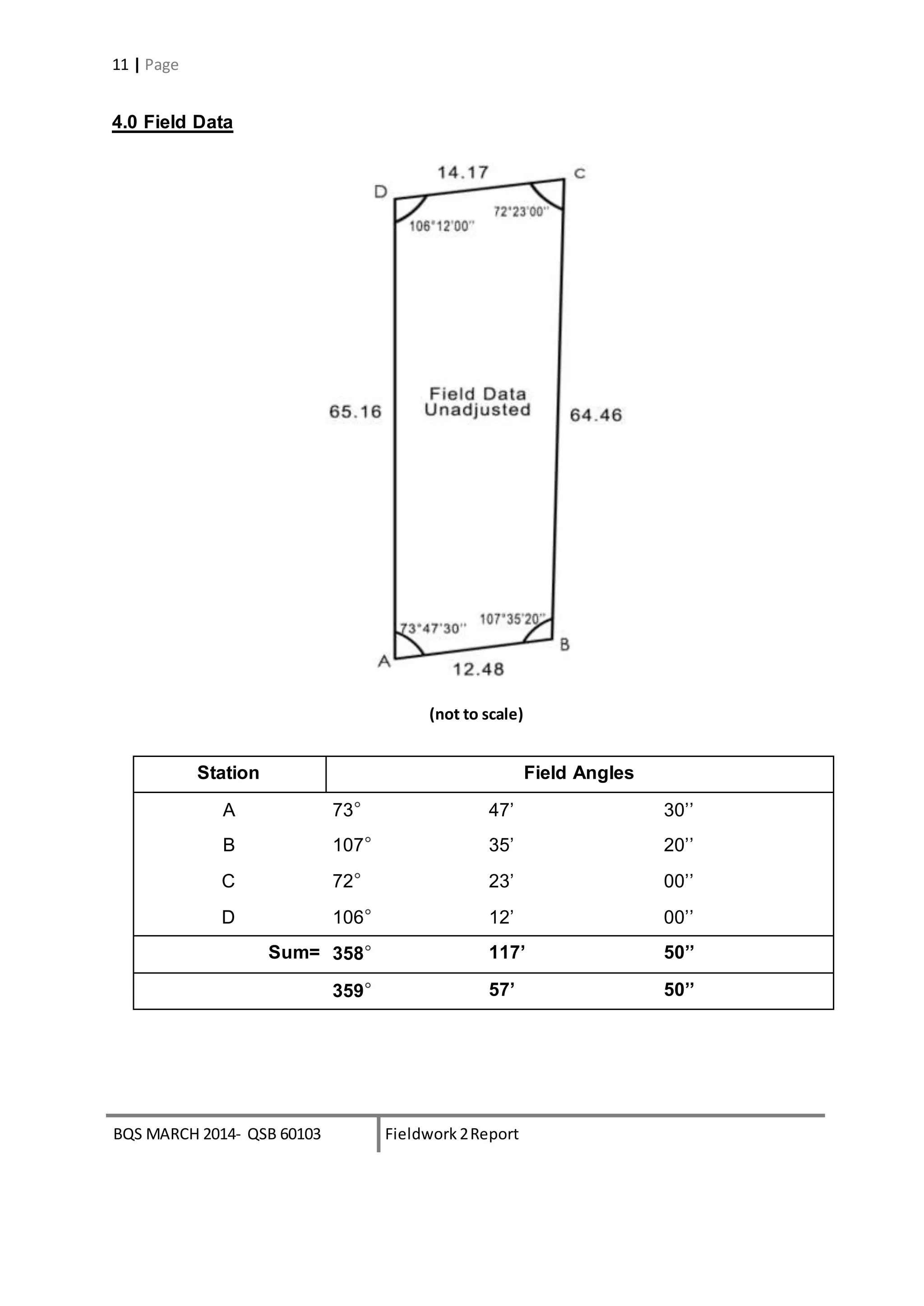
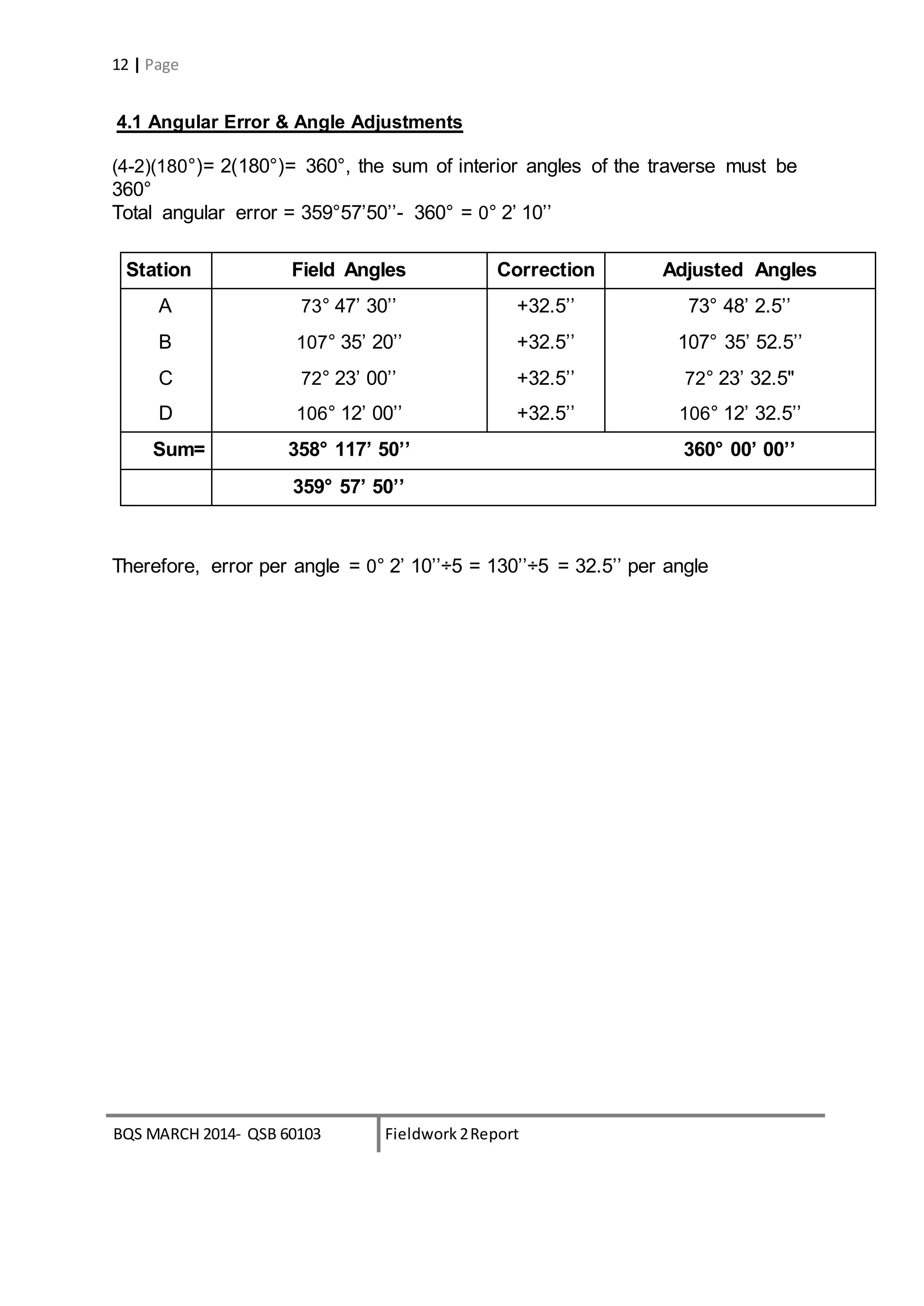
4.3 Course Latitude & Departure
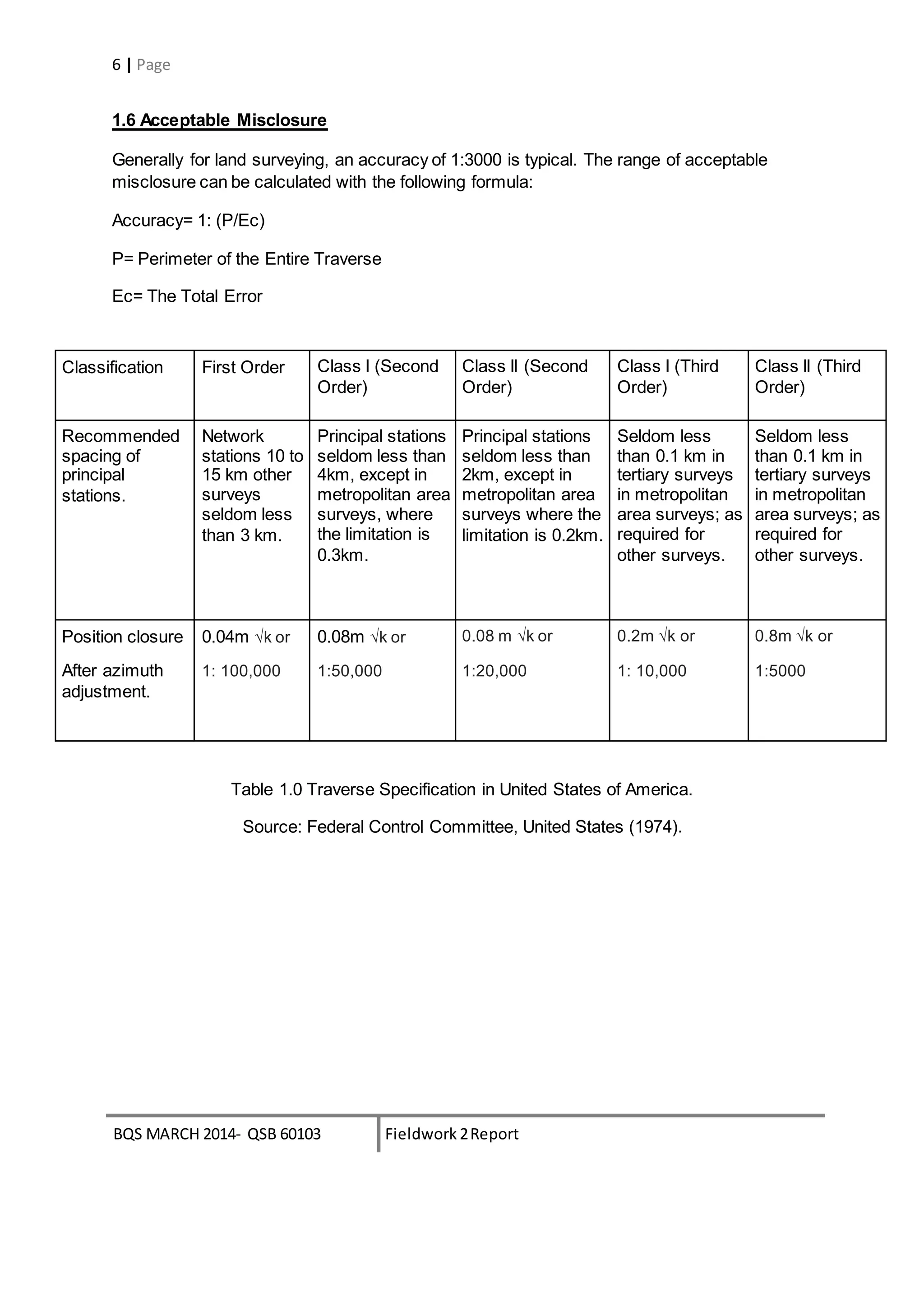
Accuracy= 1 : (P/Ec), typical=1:3000
Ec = [(sum of latitude)2 + (sum of departure)2 ]1/2
= 0.045
P = 156.27
Accuracy = 1: (156.27/0.045)
= 1: 3473
∴The traversing is acceptable
cosβ sinβ Lcosβ Lsinβ
Station Bearing, β Length, L Cosine Sine Latitude Departure
A N73° 48’ 2.5’’E 12.48 0.2789795 0.9602970 +3.4819 -11.9845
B N1°23’55’’E 64.46 0.9997021 0.024407 +65.1405 +1.5899
C N73°47’32.5’’E 14.17 -0.2791421 -0.9602498 -3.9548 -13.6060
D S0°00’00’’E 65.16 -1.00000 0.00000 -64.7000 0.0000
TOTAL 156.27 -0.0324 -0.0316

15. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
15 | Page
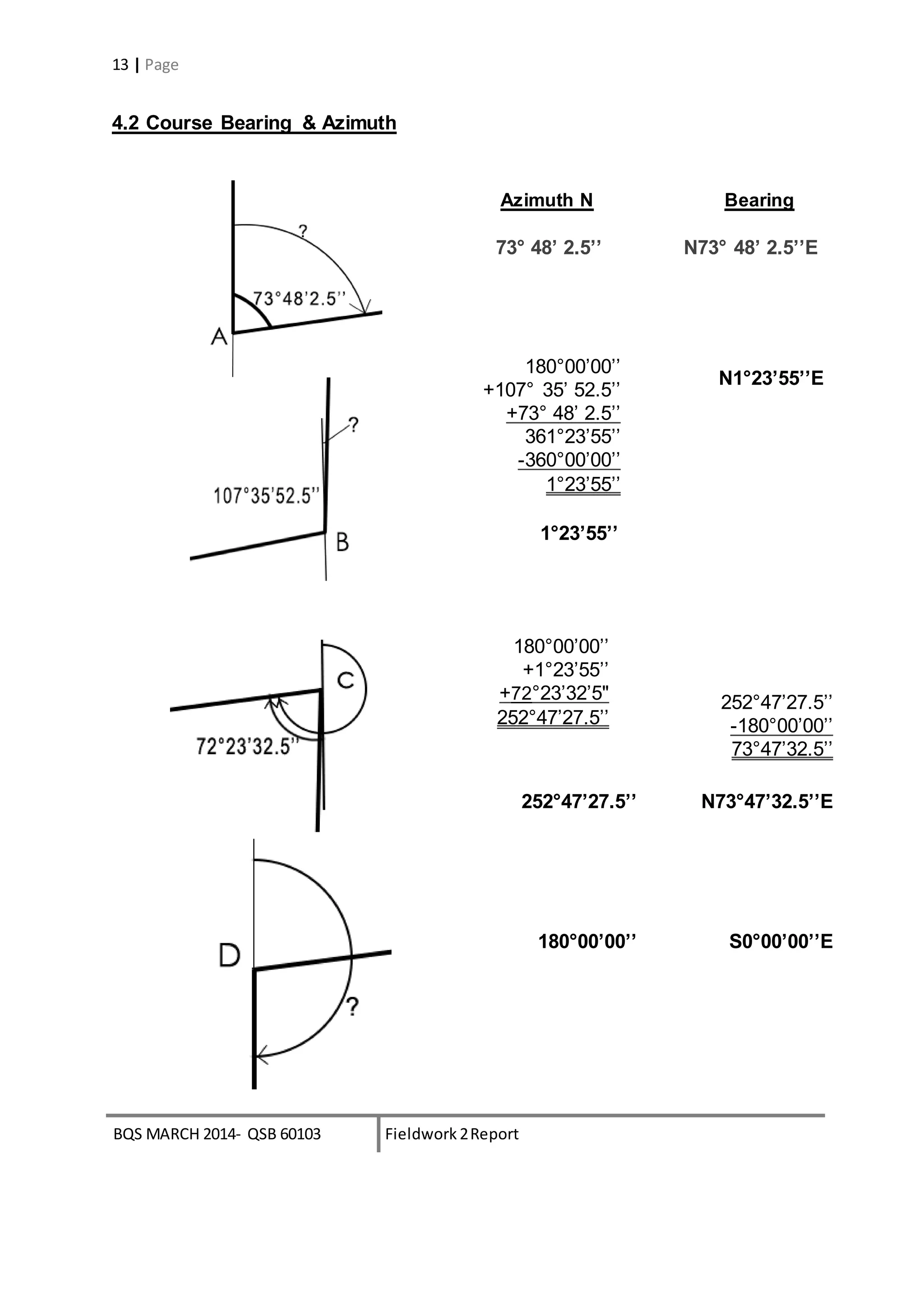
5.0 Adjusted Latitude & Departure
Compass Rule:
Correction = - [∑Δy] ÷ P x L or - [∑Δx] ÷ P x L
CorrectionAB Lat= -(-0.0324) ÷ 156.27 x 12.48
= +0.0026
CorrectionBC Lat= -(-0.0324) ÷ 156.27 x 64.46
= +0.0135
CorrectionCD Lat= -(-0.0324) ÷ 156.27 x 14.17
= +0.0029
CorrectionDA Lat= -(-0.0324) ÷ 156.27 x 65.16
= +0.0134
CorrectionAB Dep= -(-0.0316) ÷ 156.27 x 12.48
= +0.0025
CorrectionBC Dep= -(-0.0316) ÷ 156.27 x 64.46
= +0.0131
CorrectionCD Dep= -(-0.0316) ÷ 156.27 x 14.17
= +0.0029
CorrectionDA Dep= -(-0.0316) ÷ 156.27 x 65.16
= +0.0131
Unadjusted Corrections Adjusted
Station Latitude Departure Latitude Departure Latitude Departure
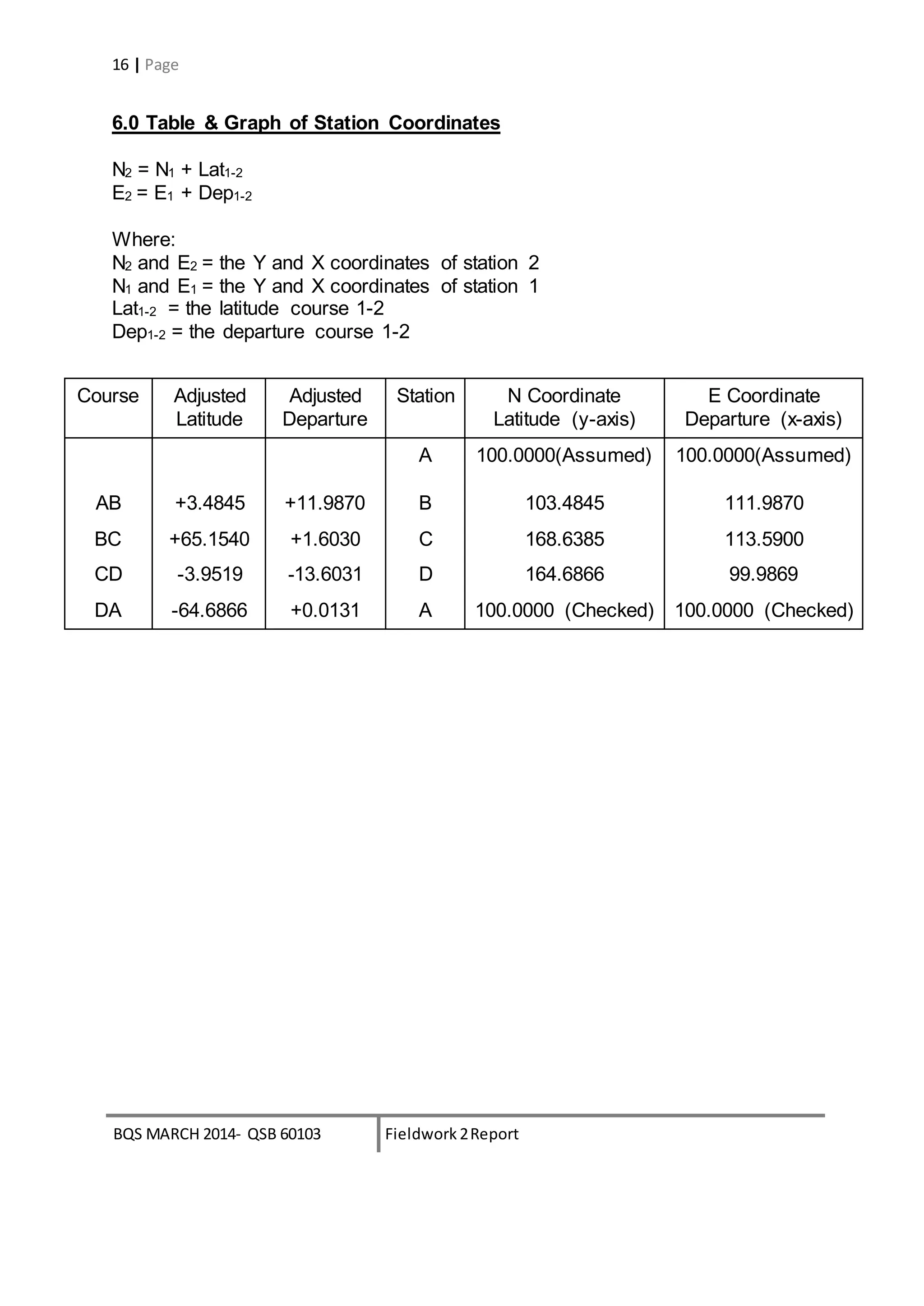
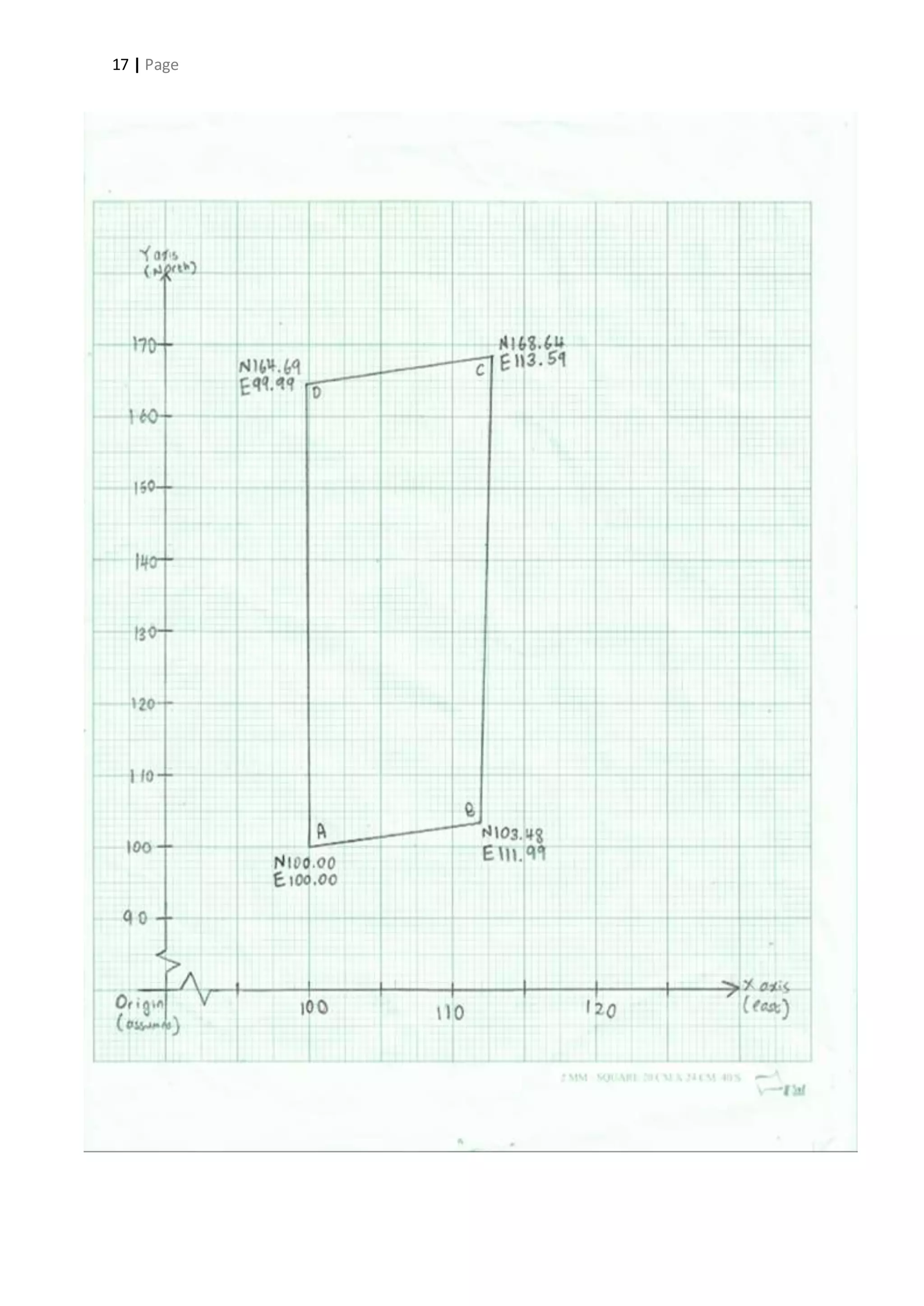
A +3.4819 -11.9845 +0.0026 +0.0025 +3.4845 +11.9870
B +65.1405 +1.5899 +0.0135 +0.0131 +65.1540 +1.6030
C -3.9548 -13.6060 +0.0029 +0.0029 -3.9519 -13.6031
D -64.7000 0.0000 +0.0134 +0.0131 -64.6866 +0.0131
Check -0.0324 -0.0316 +0.0324 +0.0316 0.00 0.00

16. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
16 | Page
6.0 Table & Graph of Station Coordinates
N2 = N1 + Lat1-2
E2 = E1 + Dep1-2
Where:
N2 and E2 = the Y and X coordinates of station 2
N1 and E1 = the Y and X coordinates of station 1
Lat1-2 = the latitude course 1-2
Dep1-2 = the departure course 1-2
Course Adjusted
Latitude
Adjusted
Departure
Station N Coordinate
Latitude (y-axis)
E Coordinate
Departure (x-axis)
A 100.0000(Assumed) 100.0000(Assumed)
AB +3.4845 +11.9870 B 103.4845 111.9870
BC +65.1540 +1.6030 C 168.6385 113.5900
CD -3.9519 -13.6031 D 164.6866 99.9869
DA -64.6866 +0.0131 A 100.0000 (Checked) 100.0000 (Checked)

17. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
17 | Page

18. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
18 | Page
7.0 Summary
In this fieldwork, closed loop traverse is being used. For our first attempt,
we shared the theodolite with another group and used the pacing method to
obtain our length of each course but we failed to get an accuracy of at least
1:3000. For our second attempt, we used the tape-measure to measure the
length of each course. In order to get the most accurate reading possible, our
lecturer, Mr.Chai taught us to use the theodolite to guide our tape-measure to
make sure it is in a straight line.
Our error in departure is -0.0316 and our error in latitude is -0.0324. The
total error is 0.045.Using the following formula, we calculated the accuracy of
our traverse survey:
Accuracy = 1: Perimeter/ Error Closure
We obtained an accuracy of 1: 3473. For average land
surveying an accuracy of 1:3000 is typical. Therefore, our traverse survey is
acceptable.
For the adjustment of latitude and departure, we used the compass rule,
using the following formula:
Correction = - [∑Δy] ÷ P x L or - [∑Δx] ÷ P x L
Where:
∑Δy or ∑Δx = the error in latitude & departure
P = The total length or perimeter of the traverse
L = The length of the particular traverse

19. BQS MARCH 2014- QSB 60103 Fieldwork 2Report
19 | Page
8.0 References
Bob Vila (n.d.). The Plumb Bob. (Website). Retrieved on 20th
November 2014 from
http://www.bobvila.com/articles/495-the-plumb-bob/#.VHbzzTGUeoh
Federal Geodetic Control Committee (1984). Standard Specifications for Geodetic Control
Networks. Retrieved on 20th
November from
http://www.ngs.noaa.gov/FGCS/tech_pub/1984-stds-specs-geodetic-control-
networks.pdf
Food and Agriculture Organization of United Nations (n.d.). Making a Site Survey. (Website).
Retrieved on 20th
November 2014 from
http://www.fao.org/docrep/v5270e/v5270e02.htm
Muskett, M. (1995). Site Surveying. (2nd
ed). Oxford, United Kingdom: Blackwell Science Ltd.
Penn State College of Earth and Mineral Sciences (2014). Land Surveying and Conventional
Techniques for Measuring Positions on the Earth’s Surface. Retrieved on 20th
November 2014 from https://www.e-education.psu.edu/geog160/node/1926