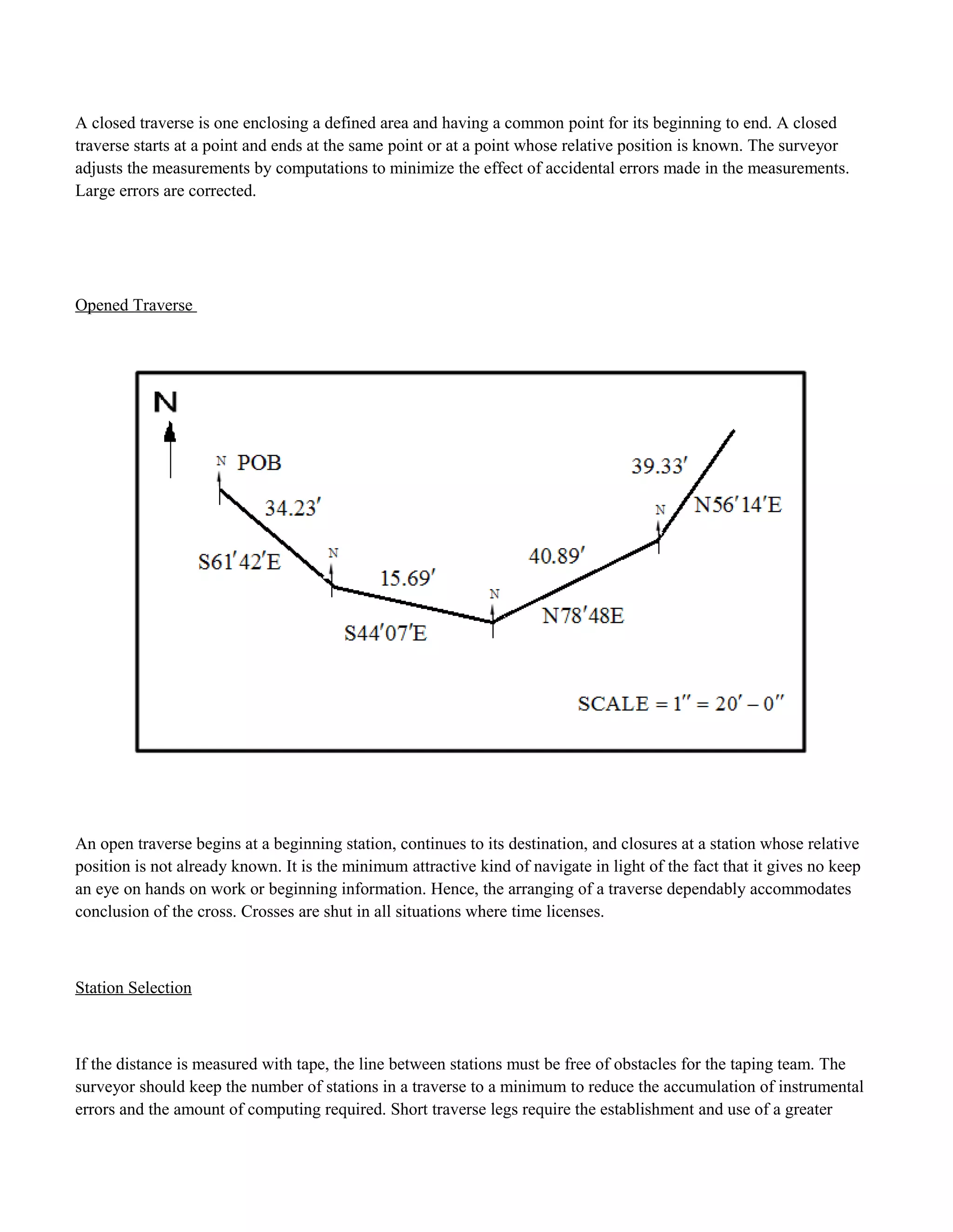
The fieldwork report details a closed traverse survey conducted by students using a theodolite. Measurements of angles and distances were taken at stations A through D. The total angular error was 0.27' and distributed evenly among measured angles. Course directions and lengths were calculated. The total error of 0.15 latitude and 0.61 departure fell within the acceptable accuracy of 1:202. Coordinates were determined for each station after applying compass rule corrections. The closed traverse allowed students to apply surveying skills and techniques learned in class.

1. SCHOOL OF ARCHITECTURE, BUILDING AND DESIGN
BACHELOR OF SCIENCE ( QUANTITY SURVEYOR )
QSB 60103 SITE SURVEYING
Fieldwork 2 Report : Traversing
Group member :
Lim Chern Yie 0315688
Leong Chee Mun 0316256
Muhammad Hasif bin Alias 0316413
Liew Yong Sheng 0315108

2. Table of Content
Introduction 2
Apparatus of Fieldwork 5
Objective 7
Field Data 8
Summary 13
Reference 14

3. Introduction
Traversing is the method of using lengths and directions of lines between points to determine positions of
the points. Traversing is normally associated with the field work of measuring angles and distances between points
on the ground. It is a prevalent strategy for reviewing. This article incorporates meaning of navigate looking over
alongside its classification,errors in crossing, checks, the finished strategy for navigating and plotting of cross
overview.
Closed Traverse

4. A closed traverse is one enclosing a defined area and having a common point for its beginning to end. A closed
traverse starts at a point and ends at the same point or at a point whose relative position is known. The surveyor
adjusts the measurements by computations to minimize the effect of accidental errors made in the measurements.
Large errors are corrected.
Opened Traverse
An open traverse begins at a beginning station, continues to its destination, and closures at a station whose relative
position is not already known. It is the minimum attractive kind of navigate in light of the fact that it gives no keep
an eye on hands on work or beginning information. Hence, the arranging of a traverse dependably accommodates
conclusion of the cross. Crosses are shut in all situations where time licenses.
Station Selection
If the distance is measured with tape, the line between stations must be free of obstacles for the taping team. The
surveyor should keep the number of stations in a traverse to a minimum to reduce the accumulation of instrumental
errors and the amount of computing required. Short traverse legs require the establishment and use of a greater

5. number of stations and may cause excessive errors in azimuth because small errors in centering the instrument, in
station marking equipment, and in instrument pointings are magnified and absorbed in the azimuth closure as errors
in angle measurement.
Meridians
Azimuth - The angular distance usually measured clockwise from the north point of the horizon to the intersection
with the horizon of the vertical circle passing through a celestial body.
Bearing - Horizontal angles measured from the meridian either east or west.

6. Apparatus for Fieldwork
1) Theodolite
2) Tripod
A Theodolite is a instrument for measuring
both horizontal and vertical angles, as used in
triangulation networks, and geo-location work.
It is a tool used in the land surveying and
engineering industry, but theodolites have
been adapted for other specialized purposes as
well.
A tripod is a portable three-legged frame,
used as a platform for supporting the weight
and maintaining the stability of some other
object. A tripod provides stability against
downward forces, horizontal forces and
moments about the vertical axis.

7. 3) Plumb bob
4) Level Rod
A plumb bob or a plunge is a weight, for
the most part with a pointed tip on the
base, that is suspended from a string and
utilized as a vertical reference line, or
plumb line. It is basically what might as
well be called a "water level".
A leveling rod is a reviewing device used to take
height estimations with the end goal of profiling
a segment of territory. There are various
fundamental outlines accessible, including
renditions for optical and computerized locating
and record keeping. This tool is also known as a
level staff, a reference to the original design, which
was simply a tall staff with measurement
markings.

8. Objective
- To determine the error of misclosure in order to determine whether the traversing is acceptable or
not.
- To allow student to experience hands on working with a theodolite.
- To enhance the students’ knowledge in the traversing procedure.
- To permit understudies to apply the hypotheses that had been taught in the classes in a hands- on
circumstance, for example, making modification for every edge and in addition the scope and
flight of each and every staff station keeping in mind the end goal to get the most exact results.
-To establish ground control in mapping

9. Field Data
Station Field Angles
A 96˚ 20' 00"
B 73˚ 14' 00"
C 88˚ 29' 00"
D 101˚ 30' 00"
Sum = 358˚ 93' 00"
359˚ 33' 00"
96˚20'00"
73˚14'00"
101˚30'00"
88˚29'00"
28.00m
B
A
C
D
34.00m
38.00m
27.00m

10. Angular Error & Angle Adjustments
( 4 - 2 ) ( 180° ) = 360°, the sum of interior angles of the traverse must be 360°.
Total Angular error = 360˚00'00" - 359˚33'00" = 0˚27'00’’
∴ Error per angle = 0˚27'00’’ ÷ 4 = 0˚6'45’’ per angle
Station Field Angles Correction Adjusted Angles
A 96˚20'00" + 6' 45’’ 96˚26'45"
B 73˚14'00" + 6' 45’’ 73˚20'45"
C 88˚29'00" + 6' 45’’ 88˚35'45"
D 101˚30'00" + 6' 45’’ 101˚36'45"
Sum = 358˚ 93'00" 360˚00'00"

11. Course Latitude & Departure
Station Bearing, β
Length,
L
Cosine
( cos β )
Sine
( sin β )
Latitude
( L cos β )
Departure
( L sin β )
A S 83˚33'15" E 34.00m 0.11226 0.99368 - 3.82 + 33.79
B N 10˚12'30" W 38.00m 0.98417 0.17723 + 37.40 - 6.73
C S 78˚23'15" W 27.00m 0.20129 0.97953 - 5.43 - 26.45
D S 00˚00'00" E 28.00m - 1.00000 0.00000 - 28.00 + 0.00
Total 127.00m 0.15 0.61
Accuracy = 1 : ( P / Ec ), typical = 1:3000
Ec = [ (sum of latitude)2 + (sum of departure)2 ]1/2
= 0.628
P = 127.00
Accuracy = 1 : ( 127.00 / 0.621 )
= 1 : 202
∴The traversing is acceptable

12. Adjusted Latitude & Departure
Compass Rule:
Correction = - [∑Δy] ÷ P x L or - [∑Δx] ÷ P x L
Correction AB Lat = - ( 0.15 ) ÷ 127.00 x 34.00
= - 0.04
Correction BC Lat = - ( 0.15 ) ÷ 127.00 x 38.00
= - 0.05
Correction CD Lat = - ( 0.15 ) ÷ 127.00 x 27.00
= - 0.03
Correction DA Lat = - ( 0.15 ) ÷ 127.00 x 28.00
= - 0.03
Correction AB Dep = - ( 0.61) ÷ 127.00 x 34.00
= - 0.16
Correction BC Dep = - ( 0.61 ) ÷ 127.00 x 38.00
= - 0.18
Correction CD Dep = - ( 0.61 ) ÷ 127.00 x 27.00
= - 0.13
Correction DA Dep = - ( 0.61 ) ÷ 127.00 x 28.00
= - 0.14
Unadjusted Correction Adjusted
Station Latitude Departure Latitude Departure Latitude Departure
AB - 3.82 + 33.79 - 0.04 - 0.16 - 3.86 + 33.63
BC + 37.40 - 6.73 - 0.05 - 0.18 + 37. 35 - 6.91
CD - 5.43 - 26.45 - 0.03 - 0.13 - 5.46 - 26.58
DA - 28.00 + 0.00 - 0.03 - 0.14 - 28.03 - 0.14
Check + 0.15 + 0.61 - 0.15 - 0.61 0.0 0.0

13. Table & Graph of Station Coordinates
N2 = N1 + Lat1-2
E2 = E1 + Dep1-2
Where :
N2 and E2 = the Y and X coordinates of station 2
N1 and E1 = the Y and X coordinates of station 1
Lat 1-2 = the latitude course 1-2
Dep 1-2 = the departure course 1-2
Station
N Coordinate
Latitude
E Coordinate
Departure
Course Adj. Latitude
Adj.
Departure
A
100.00
(Assumed)
100.00
(Assumed)
B 96.14 133.63 AB - 3.86 + 33.63
C 133.49 126.72 BC + 37. 35 - 6.91
D 128.03 100.14 CD - 5.46 - 26.58
A
100.00
(Checked)
100.00
(Checked)
DA - 28.03 - 0.14

14. Summary
Main outcome from this field work is how closed loop traverse is being used.
Theodolite is much more complicated than the normal levelling method. However, the
equipment itself provide varieties of information and function. The main aim is to get the
angle from one station to another in a closed traverse.
We learned how to apply Stadia principle by using the theodolite to get out length.
The measurement of the length from theodolite to the levelling staff is quite simple. In the
vision through theodolite, we are able to receive 3 horizontal line act as a marking (top,
middle and bottom). By subtracting the top and bottom, we are able to get the length
easily.
By applying all the method shown in this report, it clearly proved that theodolite are
able to obtain accurate data of the field with some work of adjusting. It is a relief to know
that we do not need to redo it as setting up the theodolite already consume our working
time up to 10-15 minutes.

15. References
1. Stadia Principles. (n.d.). Retrieved July 1, 2015, from
https://engineering.purdue.edu/~asm215/topics/stadia.html
2. Irvine, W. H., & Maclennan, F. (2006). Surveying for construction. New
York: McGraw-Hill.
3. Whyte, W. S., & Paul, R. E. (1997). Basic surveying. Routledge.