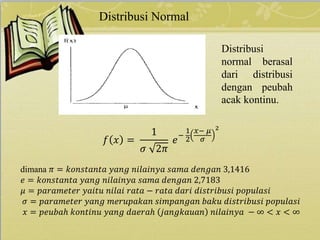
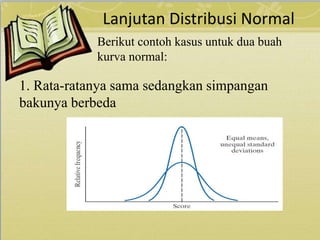
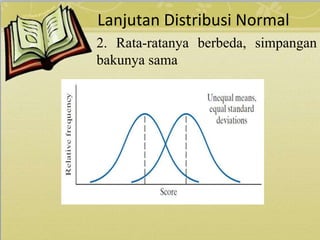
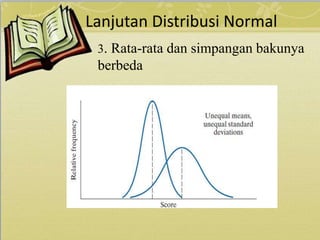
Dokumen ini membahas tentang berbagai jenis distribusi probabilitas yaitu distribusi binomial, poisson, dan normal, beserta contoh soal dan penyelesaiannya. Distribusi binomial digunakan untuk peristiwa dengan dua kemungkinan, sementara distribusi poisson model untuk kejadian dalam waktu atau ruang tertentu. Distribusi normal dicirikan oleh grafik simetris dan digunakan dalam konteks variabel kontinu dengan parameter rata-rata dan simpangan baku.